Колебания. Механические волны

Дифференциальное уравнение гармонических колебаний и его решение. Кинематика гармонических колебаний. Представление гармонических колебаний на векторной диаграмме. Сложение гармонических колебаний одного направления равных и близких частот. Сложение взаимно перпендикулярных гармонических колебаний равных и кратных частот.

Дифференциальное уравнение гармонических колебаний и его решение

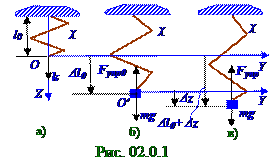
F_упр0 статической силы упругости: F_упр0 = -χΔl₀ k = -χΔl₀, где χ - коэффициент жесткости пружины. Проекция II закона Ньютонана OZ ось длятела m массой с учетом равенства нулю ускоренияэтоготела m массой при статическомрастяжении пружины имеет следующий вид:

OZ: 0 = mg - F_xупр0 ↔ 0 = mg - χΔl₀cos(Δl₀,^ k) ↔ mg = χΔl₀, (2.1)

где cos(Δl₀,^ k) = 1, т.к. вектор Δl₀статическогоудлинения пружины составляет 0º уголс

k единичным вектором(1.1) из раздела 01.0.0 "Физические основы механики".

При отклонении (рис. 02.0.1.в) кратковременнымвоздействием на величину

вектора Δzотносительно вектора Δl₀статического удлинения в пружине вместе с телом m массой возникнут гармоническиеколебания. Проекция II закона Ньютона на OZ ось в случае возникновения гармоническиеколебаний с учётом действия вектора mg силы тяжести и вектора F_упр силы упругости (1.104) из раздела 01.0.0 "Физические основы механики", а также с учётом (2.1) равенства

mg = χΔl₀, имеет следующий вид: OZ: m(d²z/dt²) = mg - F_xупр ↔ m(d²z/dt²) - mg + χΔl₀ + χΔz = 0 ↔

↔ (d²z/dt²) + ω₀²z = 0, (2.2)

где проекция Δz на OZось вектора Δzсмещения пружинного маятника заменена равной этой проекции Δz величиной z координаты, отсчитанной от O' начала координат в состоянии статического удлинения пружины, относительно которого происходит колебание этогопружинного маятника; ω₀ = (χ/m)^1/2 - циклическая частота гармонических колебаний по аналогии с (1.19) из раздела 01.0.0 "Физические основы механики"модулем ω вектора ω циклической частотыравномерного вращения - это количество полных колебанийпружинного маятника за единицу времени, умноженное на 2π радиан. Исходя из определения ω₀ циклической частоты гармонических колебаний одному полному колебанию пружинного маятникасоответствуетприращение угла, т.е. фазыколебаний, равное 2π радиан. Время T, за которое у пружинного маятника произошло приращение фазы на 2π радиан, т.е. время T, за которое этот пружинный маятник совершил одно полноеколебание, называется периодом колебаний и имеет следующий вид: T = 2π/ω₀.(2.3)

Решение линейного однородного дифференциального уравнения (2.2) 2-го порядка имеет следующий вид: z = A₁sinω₀t + A₂cosω₀t, (2.4) где A₁ и A₂ - произвольные постоянные интегрирования, определяемые из начальныхусловий.В выражении (2.4)постоянные интегрирования A₁ и A₂ определяются заданием (рис. 2.1.в) z₀ смещения пружинного маятникаотносительно l₀ статическогорастяжения этого пружинного маятникаи его проекции v_0Z на OZось вектора v₀ начальнойскорости в начальный t₀ момент времени, т.е. при

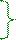t₀ = 0, которые с учётом (2.4) имеют следующий вид: z₀|_t0=0 = A₁sinω₀t₀ + A₂cosω₀t₀ = A₂ v_0Z = (dz/dt)|_t0=0 = A₁ω₀cosω₀t₀ - A₂ω₀sinω₀t₀ = A₁ω₀ ↔ A₁ = v_0Z/ω₀ .(2.5) Введем подстановку в (2.5) для A₁ и A₂ - произвольных постоянных интегрирования, имеющую следующий вид : A₁ = - Asinφ₀, A₂ = Acos φ₀ ↔ A = (A₁²+ A₂²)^1/2 ↔ φ₀ = - arctg(A₁/A₂) .(2.6) Подставим (2.6) в (2.4) и получим следующее выражение z смещения (рис. 2.1.в) тела m массой, совершающего на пружине гармонические колебания относительно статического удлинения пружинного маятника, т.е. относительно O' начала координат, в зависимости от t времени: z = A₁sinω₀t + A₂cosω₀t = Acosω₀t cosφ₀ - Asinω₀t sinφ₀ = Acos(ω₀t+ φ₀), (2.7)

где A = (A₁²+ A₂²)^1/2, φ₀ = - arctg(A₁/A₂) соответственно амплитудаи начальная фаза гармонических колебаний. Если z координата колеблющегося тела изменяется во t времени по (2.7) уравнению, то оно совершает гармоническиеколебания.

Кинематика гармонических колебаний.

Система, совершающая колебания, называется колебательной системой. Свободными колебаниями, т.е. собственными колебаниями называются колебания, которые происходят в отсутствие внешних воздействий на колебательную систему и возникают вследствие какого-либо начального отклонения этой системы от состояния её устойчивого равновесия. Колебания называются периодическими, если значения всех физических величин, характеризующих колебательную систему и изменяющихся при её колебаниях, повторяются черезравные промежутки времени. Наименьший промежутокTвремени,удовлетворяющий этому условию, называется Tпериодом колебаний. За Tпериод колебанийсистема совершает одно полное колебание. Частотойν периодических колебанийназывается величина ν = 1/T, равная числу полных колебаний, совершающихся за единицу времени. Циклической или круговой(2.2) частотой периодических колебаний, называется величина ω = 2πν = 2π/T , равная числу полных колебаний, умноженное на 2π радиан. При периодических колебаниях s отклонения физической величины от положения равновесия в зависимостиот t времени удовлетворяет следующему условию:s(t) = s(t + T). Периодические s = s(t) колебания физической величиныназываются гармоническими, если s отклонения физической величины от положения равновесия в зависимостиот t времени соответствуют следующим уравнениям: s =A cos(ωt+ φ₀) или s = A sin(ωt+ φ₁), (2.8) где ω = 2πν = 2π/T = const - циклическаяили круговаячастота гармонических колебаний; A = s_макс = const > 0 - максимальное отклонение колеблющейсяфизическойsвеличиныот состояния её устойчивого равновесия, называемое амплитудойколебаний; φ₀ и φ₁ = φ₀ + π/2 - начальные фазы колеблющейсяфизическойsвеличины. Значение физическойsвеличинывпроизвольный моментtвремениопределяется значением (2.28) фазы колебанийФ = ωt+ φ₀ или Ф = ωt+ φ₁. Величины φ₀ и φ₁ представляют собой начальные фазыколебаний, т.е. значение Ф₀ колебания физическойвеличины в момент t₀ = 0 времени. Перваяv = v(t) = ds/dt и вторая

a = a(t) = d²s/dt² производныепо времени от гармонически колеблющейся s(t) =A cos(ω t+ φ₀) физической величины также совершают гармоническиеколебания с тойже циклическойωчастотойв соответствии со следующими уравнениями: v = ds/dt = - Aωsin(ωt+ φ₀) = Aωcos(ωt+ φ₀ +π/2); (2.9) a = d²s/dt² = - Aω²cos(ωt+ φ₀) = Aω²cos(ωt+ φ₀ +π), (2.10) где v = v(t) и a = a(t) модули векторов v = v(t), a = a(t) соответственно скорости и ускорения колеблющейсяфизической s = s(t)величины; Aω и Aω² - амплитуды соответственно модулей v(t) скорости и a(t) ускоренияколеблющейсяфизическойвеличины.Из сравнения (2.8) и (2.9) начальная фаза модуля v(t) = ds/dtскорости колеблющейсяфизической s(t)величины опережает начальную фазуэтой самой физической s(t)величинына π/2 угол. Из сравнения (2.8) и (2.10) начальная фаза модуля a(t) = d²s/dt² ускорения колеблющейсяфизической s(t)величины опережает начальную фазуэтой самой физическойs(t) величинынаπ угол.

На рис. 02.0.2 построены графики физической s(t)величины- сплошной линией, ds/dtскорости - штриховой линией и d²s/dt² ускорения- штрих -пунктирнойлинией колебаний относительно

Представление гармонических колебаний на векторной диаграмме

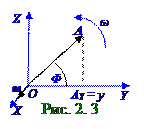
ПроекцияA_Y вектора A на горизонтальнуюOY ось совершает гармоническиеколебания по (2.7) закону, имеющая следующее выражение: A_Y = y = Acos(ωt+ φ₀), (2.11)

где (рис.2.3) проекцияA_Y вектора A на горизонтальнуюOY ось численно равна в данный момент

t времени yкоординате концаэтого A вектора.

Графическое изображение гармонических колебанийпосредством вращающегося вектора называется методом векторной диаграммы.

Согласно формуле Эйлера e^iφ = cosφ + isinφ для комплексныхчисел, где i - мнимая единица, гармонические колебания(2.7), записанные в экспоненциальной форме, имеют следующий вид: ỹ = Aexpi(ωt+ φ₀) = Ãexpiωt, (2.12) где Ã = Aexpiφ₀ -комплексная амплитуда. Действительная часть комплексной ỹ функции, обозначаемая Re ỹ, соответствует (2.7) уравнениюгармонических колебанийи имеет следующее выражение: Reỹ = y = Acos(ωt+ φ₀),(2.13) где в отличие от (рис.2.1) гармоническиеколебания происходят не по OZ, а по OY оси координат.

Сложение гармонических колебаний одного направления равных и близких частот

Под сложением колебанийпонимают нахождение уравнения, согласно которому в произвольный момент t времени определяют результирующееотклонение колеблющейсясистемы от положения равновесия, когда эта система одновременно участвует в несколькихколебательных процессах.

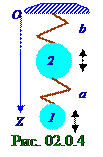
Грузик 1 - ый (рис. 02.0.4) колеблется на aпружинеотносительно 2- го грузикапо следующему уравнению: z₁ = A₁ cos(ω₁ t+ φ₁), (2.14) где z₁ - координата 1 - го грузика, т.е. отклонение от положения равновесия 1 - го грузикав зависимости от t времени в системе координат, связанной со 2 - ым грузиком; A₁ и ω₁ - соответственно (2.2) амплитудаи циклическаячастотагармоническихколебаний 1 - го грузикана а пружине относительно 2- го грузика; φ₁, рад - начальная фазаприколебаниях 1 - го грузика на

aпружинеотносительно 2- го грузика, определяющее z₁₀ координату 1 - го грузика в системе координат, связанной со 2 - ым грузиком, в начальный момент t₀ времени, т.е. когда t = t₀ = 0.

Грузик 1 - ый (рис.2.4) колеблется на bпружиневместе со 2 - ым грузикомпо следующему уравнению: z₂ = A₂ cos(ω₂t+ φ₂ ), (2.15) где z₂ - координата 1 - го грузика, т.е. отклонение от положения равновесия 1 - го грузикав зависимости от t времени, когда он колеблется как единое целое со 2 - ым грузиком на bпружинеотносительно O начала координат; A₂ и ω₂ - соответственно амплитудаи циклическая(2.2) частотагармонических колебаний 1 - го и 2- го грузиковна b пружине относительно O начала координат; φ₂, рад - начальная фазаприколебаниях 1 - го грузика на bпружинекак единое целое со 2 - ым грузиком относительно O начала координат, определяющее z₁₀ координату 1 - го грузика

в данный момент t времени.