Вращающийся Aвектор, равный сумме векторов A1 иA2 , изображающих соответственногармонические колебания1 - го грузикаотносительно 2- го грузикаи гармонические колебания 5 страница

Модули F_{yn+ Δs}, |F_yn|векторов соответственно F_{yn+ Δs} силы упругой деформации в правой чёрнойстенки с y_n+ Δs координатой и F_y силы упругой деформации у левой зелёнойстенки с y_n координатой, имеют с учётом (2.91) следующие значения: F_{yn+ Δs} = Sσ_{yn+ Δs}; |F_yn|= Sσ_yn,(2.93) где σ_{yn+ Δs}, σ_yn- напряжения(2.91), (2.93) в площадях поперечного сечения тонкого стержня, расположенных соответственно y_n+ Δs и y_n координатах, которые имеют положительные значения, поскольку малый ΔV объем тонкого стержняΔs длиной (рис. 02.0.22) во всех своих площадях поперечного сечения расширяется.

Подставляем (2.93) в (2.92) и получаем следующее выражение проекции II закона Ньютонана OY осьдля m массы материала тонкого стержня ρплотностью, заключённой в (рис.2.22) малом объеме ΔV=SΔs:

OY: ρSΔs(∂²s/∂t²) = F_{yn+ Δs} - |F_yn|↔ ρSΔs(∂²s/∂t²) = S(σ_{yn+ Δs} - σ_yn) ↔ ρΔs(∂²s/∂t²) = σ_{yn+ Δs} - σ_yn.(2.94)

На малом промежутке от y_n до y_n+ Δs координат тонкого стержня σ(y)функция, которая представляет собой σ, Н/м² напряжение в S площади, расположенной в y_n ≤ y ≤ y_n+ Δs координате этоготонкого стержня, и σ'(y) производная от σ, Н/м² напряжения непрерывны, поэтому согласно теореме Лагранжа для разности σ_{yn+ Δs} - σ_yn напряжений, имеет место следующее выражение:

σ_{yn+ Δs} - σ_yn = (∂σ/∂у)[( y_n+ Δs) - y_n] ↔ σ_{yn+ Δs} - σ_yn = (∂σ/∂у)Δs.(2.95)

Подставляем (2.90) в (2.95) и получаем следующее выражение для разности

σ_{yn+ Δs} - σ_yn напряжений в площадях поперечного сечения тонкого стержня, расположенных соответственно y_n+ Δs и y_n координатах, т.е. (рис.2.22) в левой зелёнойи правой чёрной стенках малого ΔV объема тонкого стержняΔs длиной, испытывающего в момент t_n времени расширение: σ_{yn+ Δs} - σ_yn = (∂σ/∂у)Δs ↔ σ_{yn+ Δs} - σ_yn = E[∂(∂s/∂y)/∂y]Δs ↔ σ_{yn+ Δs} - σ_yn = E(∂²s/∂y²)Δs.(2.96)

Подставляем (2.96) в (2.94) и получаем по аналогии с (2.84) акустической волнойследующее одномерное волновое уравнениераспространения продольных волнвлинейной однородной изотропной непоглощающей упругой среде:

E(∂²s/∂y²)Δs = ρΔs(∂²s/∂t²) ↔ ∂²s/∂y² = (ρ/E)(∂²s/∂t²) ↔∂²s/∂y² = (1/v²)(∂²s/∂t²), (2.97) где (E/ρ)^1/2 = v- фазовая(рис.2.21) скоростьраспространения продольной волнывлинейной однородной изотропной непоглощающей упругой среде в направлении k волнового вектора, перпендикулярного плоской поверхности S площадью поперечного сечения тонкого стержня.

Волновое уравнение, фазовая скорость распространения поперечных волн в гибком шнуре

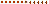
этого гибкого шнура.

Упругая поперечнаяволна в (рис. 02.0.23) натянутом с F силой гибком шнуре представляет собой последовательность малых s отклонений площади поперечного сечения гибкого шнура относительно положения равновесия в направлении k волнового вектора, т.е. вдоль этого гибкого шнура в положительную сторону OY оси.

Вследствие колебаний c (2.3) T = 2π/ω периодомгармонических колебаний (рис. 02.0.23) внешнего И источника,например, вибратора, y₀-y₁ отрезок гибкого шнура, находящегося между поперечными сечениями этого гибкого шнура с y₀, y₁ координатами соответственно, в интервал времени от 0 до T/4 отклоняется вверх, т.е. в положительную сторону OZ оси. Участок гибкого шнура с y₀ координатой в момент t₁ = T/4 времени отклоняется (рис. 02.0.23) по OZ оси относительно положения равновесия на s_m максимальное или амплитудное значение.

В интервал (рис. 02.0.23) времени от T/4 до T/2 y₀-y₁ отрезок гибкого шнура, находящегося между поперечными сечениями этого гибкого шнура с y₀, y₁ координатами соответственно, отклоняется вниз и в момент t₁ = T/2 времени участок гибкого шнура с y₀ координатой занимает положение равновесия.

Участок (рис. 02.0.23) гибкого шнура с y₁ координатой, вследствие наличия поперечных сил упругой деформации, приобретает от участков гибкого шнура, находящихся на y₀-y₁ отрезке, т.е. от участков гибкого шнура, в котором происходит волновойпроцесс, вектор начальной скорости, направленный в положительную сторону OZ оси. Вследствие этого участок (рис. 02.0.23) гибкого шнура с y₁ координатой в момент t₁ = T/2 времени отклоняется по OZ оси относительно положения равновесия на s_m максимальное или амплитудное значение.

Согласно (рис. 02.0.2) представлению колебаний векторными диаграммами одному периоду

T = 2π/ω, где ω – циклическая частота гармонических колебаний, создаваемых Иисточником, соответствует приращение фазыколебаний этого И источникана 2π угол.

За время Tпериодагармонических колебаний И источникапоперечная волна (рис. 02.0.23) распространится вдоль гибкого шнура на расстояние от этого И источника, равноеλдлине поперечной волны. За время распространения поперечнойволны на λ расстояниеИ источник гармонических колебаний изменит фазусвоих колебаний на угол 2π. Поэтому частицы в площади поперечного сечениягибкого шнура, имеющие расстояние между собой, равное λдлине волныи имеющие одинаковыеs отклонения относительно положения равновесия, имеют различие по фазеколебаний этих частиц, равное 2π.

На рис. 02.0.24 по аналогии с рис. 02.0.22, где изображеноприращениетонкого стержнямалого ΔV объема Δy длиной и S площадью поперечного сечения, при распространении в нём продольной упругой волны,представлена отдельно от всего (рис. 02.0.22) гибкого шнура Δy малая деформированнаядлина этого гибкого шнура, испытывающего, например, в момент t_n времени отклонение относительно положения равновесия вверх, т.е. в положительную сторону OZ оси, на малую Δs величину. Вследствие малых Δs величин отклонений относительно положения равновесия частиц в площади поперечного сечениягибкого шнура, имеет место следующее выражение: ∂s/∂y = tgα ≈ sinα,(2.98)

где (рис. 02.0.23) α - малый угол отклонений площадей поперечного сечениягибкого шнура относительно положения равновесия при распространении в нём поперечной упругой волны.

Модуль F вектора F силы натяжения гибкого шнура при распространении в нём поперечной упругой волны постоянен, т.е. не зависит от y координаты площади поперечного сечения

F(y_n) силы реакции, имеющий проекцию F_Z(y_n) на OZ ось, а стороны правойчасти гибкого шнура приложен в y_n+ Δy координате вектор F(y_n+ Δy) силы натяжения, имеющий проекцию F_Z(y_n+ Δy) на OZ ось. Векторы F(y_n), F(y_n+ Δy) соответственно сил реакции, натяжения имеют равные F модули, но различные по причинедеформациималой Δy длины гибкого шнура проекции F_Z(y_n), F_Z(y_n+ Δy) на

OZ ось этих сил реакции, натяжения. Вследствие (рис. 02.0.24) этой деформациималой Δy длины гибкого шнура (рис. 02.0.23) малые α углы наклона относительно OY оси векторов F(y_n), F(y_n+ Δy)соответственно сил реакции, натяжения, направленных по касательной к деформированноймалой Δy длинегибкого шнура, различны и зависят от y_n, y_n+ Δy координатсоответственно началаи конца деформированноймалой Δy длиныгибкого шнура.

В площади поперечного сечениягибкого шнура, находящемся в малом промежутке от

y_n до y_n+ Δy координат соответственно началаи конца деформированноймалой Δy длиныгибкого шнура, F_Z(y)функция, которая представляет собой проекцию F_Z(y) на OZ ось вектора F(y) силы натяжения в этой S гибкого шнура, и F_Z '(y) производная от F_Z(y)функции непрерывны. Поэтому согласно теореме Лагранжа приращение F_Z(y_n+ Δy) - |F_Z(y_n)|функции F_Z(y) на малом промежутке от y_n до y_n+ Δy координат имеет место следующее выражение: F_Z(y_n+ Δy) - |F_Z(y_n)| = (∂F_Z /∂у)Δy,(2.100) где (рис. 02.0.24) "- |F_Z(y_n)| " - отрицательноезначение (рис. 02.0.24) проекции F_Z(y_n) на OZ ось вектора F(y_n) силы реакции в площади поперечного сечениягибкого шнура, расположенной в y_n координате начала деформированноймалой Δy длиныгибкого шнура.

Проекция II закона Ньютонана OZ осьдля m массы материала гибкого шнура ρ_п погонной

плотностью, заключённой в (рис. 02.0.24) малой Δy длинегибкого шнура, к которой приложены два вектора: вектор F(y_n) силы реакции вначале деформированной малой Δy длиныгибкого шнура и F(y_n+ Δy силы натяжения в y_n+ Δy координате конца деформированноймалой Δy длиныэтого гибкого шнура, имеет с учётом (2.100) следующий вид: OZ: ρ_пΔy(∂²s/∂t²) = F_Z(y_n+ Δy) + F_Z(y_n) ↔

↔ ρ_пΔy(∂²s/∂t²) = F_Z(y_n+ Δy) - |F_Z(y_n)| ↔ ρ_пΔy(∂²s/∂t²) =(∂F_Z /∂у)Δy↔ρ_п(∂²s/∂t²) =(∂F_Z /∂у), (2.101)

где ρ_п = ρ/S , кг/м - погонная плотность гибкого шнура, имеющего S площадь поперечного сечения и

ρплотностьматериала, из которого изготовлен этот гибкий шнура; погоннаяρ_пплотность протяжённогопредмета-этомассаединицыдлины этого протяжённогопредмета;∂²s/∂t² - проекция вектора ∂²s/∂t² ускоренияна OZ ось (рис. 02.0.24) центраC деформированной малой Δy длиныгибкого шнура при его перемещениина малое s отклонение относительно положения равновесия по OZ оси.

Подставляем (2.99) в (2.101) и получаем по аналогии с (2.97) продольными волнамивлинейной однородной изотропной непоглощающей упругой среде следующее одномерное волновое уравнениераспространения поперечных упругих волны вгибком шнуре, вдоль длины которого приложенвектор F силы натяжения с F модулем:

ρ_п(∂²s/∂t²) =∂[F(∂s/∂y)]/∂у ↔ ρ_п(∂²s/∂t²) =F∂[(∂s/∂y)]/∂у ↔

↔ ∂²s/∂y² = (ρ_п/F)(∂²s/∂t²) ↔ ∂²s/∂y² = (1/v²) (∂²s/∂t²),(2.102) где (F/ρ_п)^1/2 = v- фазовая(рис. 02.0.23) скоростьраспространения поперечных упругих волны вгибком шнуре, натянутого с F силой и имеющего ρ_п погонную плотность, в направлении k волнового вектора вдоль длины этого натянутогогибкого шнура.

Давление звука, интенсивность звуковой волны. Объемная плотность энергии упругих волн

Звуковое давление- это давление, возникающее при прохождении звуковой волныв жидкойи газообразной средах. Оно представляет собой переменную часть давления, т.е. колебания давления относительно среднего значения при прохождении звуковых волнв среде. Звуковое давление - главная количественная характеристика звука, основной объект акустических измерений. Единица измерения звукового давленияв СИ - Ньютон на квадратный метр(Н/м²). Действующее значение звукового давления в воздухе изменяется в широких пределах - от 10^-5 Н/м² вблизи порога слышимостидо 10³ Н/м² при самых громких звуках, например, шумах реактивного самолета. В воде на ультразвуковых частотахпорядка нескольких МГц с помощью фокусирующих излучателей получают значение звукового давлениядо 10⁷Н/м².

В некоторой среде распространяется в направлении OY осиплоская продольная волна. В элементарном ΔV объёме частицы упругой средысовершают гармоничекие колебания, т.е

s отклонения(2.69) от положения равновесия впроизвольный момент tвремени. Скорость∂s/∂t отклоненийs от положения равновесия частиц упругой среды в произвольный моментt времени и их (2.90) относительная∂s/∂yдеформация от этого положения равновесия, определятся из (2.79) для плоской синусоидальной волны, распространяющейся вдоль положительного направления OY оси, из следующего выражения: ∂s/∂t = -Aωsin(ωt - ky+ φ₀); ∂s/∂y = Aksin(ωt - ky+ φ₀). (2.103) КинетическаяΔW_kэнергияв элементарном ΔV объеме m = ρΔV массой, где ρ - плотность упругой среды, имеющей впроизвольный моментt времени ∂s/∂t скорость колебаний, с учетом (1.83) из раздела 01.0 "Физические основы механики" и (2.103) определяется из следующего выражения: ΔW_k = (ρΔV/2)( ∂s/∂t)² = (ρΔV/2) A² ω² sin² (ωt - ky+ φ₀). (2.104) ПотенциальнаяΔW_pэнергияв элементарном ΔV объеме, имеющего (2.90) относительную∂s/∂yдеформациюдлины этого ΔV объема по OY оси с учетом связи фазовойvскорости продольной упругой волныс модулемE Юнга: E = ρv², а также с учётом и связи k волнового числа c циклическойωчастотойи фазовойvскоростью: k = ω/v, имеет следующий вид:

ΔW_p = (EΔV/2)(∂s/∂y)² = (ρΔVv²/2) A²k ²sin²(ωt - ky + φ₀) = (ρΔV/2) A²ω²sin²(ωt - ky+ φ₀). (2.105) Сумма (2.104) и (2.105) с делением на элементарный ΔV объём упругой средыприводит к следующему выражению wобъемной плотности энергии бегущей продольной волны, т.е.энергии, содержащейся в единице объема упругой среды, в которой распространяется бегущая продольная волна: w = (ΔW_k + ΔW_p)/ΔV = ρA²ω²sin²(ωt - ky+ φ₀).(2.106) В случае поперечнойволны дляwобъемной плотности энергииполучается выражение, аналогичное (2.106). Из (2.106) следует, чтоwобъемная плотность энергии бегущей продольнойили поперечной волныв каждый момент t времени в разных точках пространства различна. В одной и той же точке пространства, а для одномерного случая при одной и той же y = const координате согласно (2.106) wобъемная плотность энергии бегущей продольнойили поперечной волныв упругойсреде изменяется с t временем пропорционально квадрату синуса. Среднее значение квадрата синуса равно1/2, поэтому <w> среднее по t временизначение wобъемной плотности энергии бегущей продольнойили поперечной волны в каждой точке упругой среды определяется из следующего выражения: <w> = ρA²ω²/2. (2.107)

Вектор Умова - вектор плотности потока энергии упругих волн

Вектор v скорости переносаэнергии волной равен вектору v скорости перемещения в пространстве поверхности, соответствующей максимальному значению wобъемной плотности энергии бегущей продольнойили поперечной волны в упругойсреде. Вектор v скорости переносаэнергии для синусоидальныхволн коллинеарен (рис. 02.0.17) k волновому векторураспространения волны в упругой среде сvфазовой скоростьюи направлен этот вектор v скорости переносаэнергии в одну сторону с k волновым вектором.

Энергия dW синусоидальной волны, проходящая (рис. 02.0.25) черезэлементарную поверхностьdS площадью упругой среды, которая расположена под α углом к направлению вектора v скорости переносаэнергии волной, т.е. расположена под α углом к направлению k волнового вектора, за элементарный промежуток dt времени определяется из следующего выражения: dW = wvdScosαdt= w(vdS)dt = wdS(vn)dt, (2.108) где vdScosα -объёмэнергии, прошедшей черезэлементарную поверхность dS площадью упругой средыза единицуt временив направлении вектора v скорости переносаэнергии волной;

w -объемная плотность энергии бегущей продольнойили поперечной волны в упругойсреде; n - единичный векторнормали к элементарной поверхностиdS площадью упругойсреды; α - угол междук элементарной поверхностиdS площадью упругойсредыи вектором v скорости переноса энергииволной.

где u = wv - вектор плотности потока энергии волны в упругойсреде, который направлен в сторону переноса (2.108) энергии dW синусоидальной волны и называется вектором Умова.ИнтенсивностьюIволныназывается модуль среднего значения по t времени вектора Умова.ИнтенсивностьIволнычисленно равна энергии W синусоидальной волны, переносимой волной за единицуt временисквозь поверхностьединичнойплощадью, нормальной к направлению распространению волны, т.е. расположенной нормальнок направлению k волнового вектора.

С учетом выражения (2.109)вектора u плотности энергии бегущей продольнойили поперечной волны в упругойсреде, а также с учётом выражения (2.108) <w> среднего по t временизначения wобъемной плотности энергии бегущей продольнойили поперечной волныв упругойсреде выражение для Iинтенсивности этих волн имеет следующий вид:

I = |<u>| = v<w> = ρvA²ω²/2 кг/с³(Вт/м²).(2.110)

Когерентные волны в упругой среде. Интерференция этих волн

Двебегущие продольныеили поперечные волны в упругойсреде называются когерентными, если по аналогии с (2.20) разность их фаз (2.72) Ф₂ – Ф₁ в точке упругой среды с y координатой не зависит от времени и имеет следующий вид: Ф₂ – Ф₁ = (ω₂t - ky+ φ₂) - (ω₁t - ky+ φ₁) = const,(2.111) где ω₁ и ω₂ - циклическая частота гармонических колебаний (рис. 02.0.16), создаваемых соответственно

И₁ и И₂ источникамикогерентных(2.20) колебаний, вследствие чего в точке упругой среды с

y координатой в данныймомент tвремени существуют когерентныеволны;φ₁ и φ₂ – начальные(2.8) фазы колебаний в t₀ = 0 моментвремени частиц упругой среды в точке с y = 0 координатой, т.е. вПл.1плоскостиравных фаз, где находятся (рис. 02.0.16)соответственно И₁ и И₂ источникигармонических когерентных(2.20) колебаний в упругойсреде.