Влияние сопротивления на вынужденные колебания.

Рассмотрим движение материальной точки вдоль оси 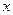под действием линейной восстанавливающей силы 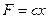, силы линейно – вязкого сопротивления 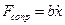и гармонической вынуждающей силы 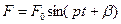. Составим дифференциальное уравнение движения

.

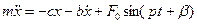Оно может быть переписано в виде

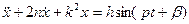, (1.20)

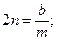
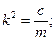
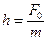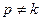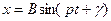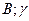где - постоянные коэффициенты. Это неоднородное дифференциальное уравнение второго порядка, решение которого есть сумма решений однородного уравнения (1.12) и частного решения уравнения (1.20). В случае, когда , последнее будем искать в виде , где - неизвестные постоянные. Подставим выражений для 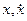и 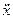в неоднородное уравнение (1.20) и приравняем коэффициенты при одноименных тригонометрических функциях в левой и правой частях уравнения. Получим систему из двух алгебраических уравнений, решив которую найдем неизвестные величины

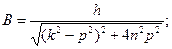
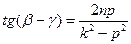. (1.21)

Тогда общее решение неоднородного уравнения запишется как

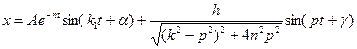, (1.22)

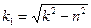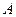где , а и 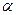- постоянные величины, определяемые из начальных условий. Через некоторый промежуток времени в результате действия силы сопротивления, в решении (1.22) остается только последнее слагаемое, характеризующее вынужденные установившиеся колебания. При этом перемещение материальной точки будет сдвинуто по фазе относительно вынуждающей силы на угол 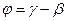. На рис.1.13 приведены амплитудно-частотная и фазово-частотная характеристики этого движения.

Рис.1.13

Отметим несколько особенностей: наличие сопротивления делает амплитуду вынужденных колебаний при резонансе конечной, а частота, при которой наблюдается максимум, смещается в сторону начала координат; с ростом сопротивления величина амплитуды уменьшается. Уже при значении 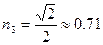явно выраженный максимум отсутствует. Сдвиг фаз между перемещением материальной точки и вынуждающей силой при фиксированном сопротивлении будет постоянной величиной, определяемой частотами свободных колебаний и вынуждающего воздействия (см. формулы (1.21)).