Выявление условий возникновения и исследование резонанса токов в цепи синусоидального тока при параллельном соединении катушки индуктивности и батареи конденсаторов.

· Общие сведения

Резонанс токов может возникнуть в цепи синусоидального тока при параллельном соединении ветвей с индуктивным L и емкостном Сэлементами.

При этом дополнительный резистивный элемент R может быть включен в цепь также параллельно, или последовательно, или вовсе отсутствовать. В данной работе исследуется резонанс токов в цепи с параллельным соединением R,L,C –элементов, как показано на схеме замещения рис. 3.39.

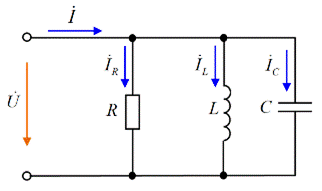
Рис. 3.39. Схема замещения цепи синусоидального тока
с параллельным соединением R,L,C-элементов

Полный ток в этой цепи определяется согласно закону Ома по формуле:

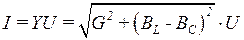(3.88)

где G = 1/R – активная проводимость; B_L = 1/X_L – реактивная индуктивная проводимость; B_C = 1/X_C – реактивная емкостная проводимость; Y = 1/Z – полная проводимость цепи синусоидального тока с параллельным соединением R,L,C –элементов; ½B_L − B_C½ = B – общая реактивная проводимость.

Из формулы (3.88) видно, что действующее значение тока в неразветвленной части цепи зависит от активной G и реактивной В проводимостей и от напряжения U сети, подведенного к зажимам цепи.

Режим работы цепи синусоидального тока с параллельно соединенными индуктивностью L и конденсатором C, при котором угол сдвига фаз j = y_u − y_i между напряжением U сети и током I в неразветвленной части цепи равен нулю называется резонансом токов.

Условием возникновения резонанса токов является равенство реактивной индуктивной проводимости B_L и реактивной емкостной проводимости В_С :

B_L = B_C.

Поскольку B_L = 1/X_L и B_C = 1/X_С, то при условии их равенства вытекает равенство индуктивного X_L и емкостного X_С сопротивлений:

Х_L = Х_C,

которое также является условием возникновения резонанса токов в цепи с параллельным соединением L,C –элементов

Характерные особенности цепи синусоидального тока при резонансе токов.

1. Так как B_L = B_C , то при резонансе токов, как следует из (3.88) полная проводимость Y_рез равна активной проводимости G и принимает минимальное значение:

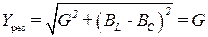= G. (3.89)

2. В то же время, полное сопротивление этой цепи при резонансе токов имеет максимальное значение, равное активному сопротивлению:

Z_рез = 1/Y_рез = 1/G = R. (3.90)

3. Так как Z_рез = max, а Y_рез =min, то при резонансе ток в неразветвленной части цепи, т.е. полный ток I имеет минимальное значение:

I_рез = U/Z_рез = Y_резU = GU. (3.91)

Это свойство позволяет обнаруживать резонанс токов в цепи синусоидального тока с параллельными L,C-элементами при изменении частоты ω или параметров L и C.

4. Так как при резонансе B_L = B_C , I_рез = GU, то действующее значение токов в ветвях с индуктивным и емкостным элементами (рис. 3.39), т.е. реактивные токи I_L и I_C , равны по модулю и могут превышать ток в неразветвленной части цепи в B_L/G раз (если B_L = B_C > G):

I_L = I_C ; (3.92)

I_L = B_LU = B_LI_рез/G, (3.93а)

I_C = B_CU = B_CI_рез/G. (3.93б)

При этом угол сдвига фаз между токами равен p = 180°, так как в индуктивном элементе ток отстает от напряжения по фазе на угол p/2 , а ток в емкостном элементе опережает напряжение на тот же угол.

Действующее значение тока I_R в ветви с резистивным элементом R (рис. 3.39), т. е. активная составляющая тока при резонансе токов, равна току в неразветвленной части цепи:

I_R = I_а = I_рез. (3.94)

Многократное усиление токов в параллельных ветвях с индуктивным L и емкостным С элементами при неизменном общем токе в неразветвленной части цепи является важной особенностью резонанса токов и широко используется в радиотехнических устройствах и установках автоматики.

5. Так как при резонансе токов угол сдвига фаз между напряжением и током в неразветвленной части цепи равен нулю (j = 0), то коэффициент мощности такой цепи равен единице:

cosj = I_R/I = P/S = G/Y = R/Z = 1. (3.95)

Из выражения (3.41) следует, что полная мощность при резонансе токов равна активной мощности:

S = YU² = GU² = P. (3.96)

6. Так как при резонансе токов B_L = B_C , Q_L = B_LU² и Q_C = B_CU², то

Q_L = Q_C, (3.97)

т.е. при резонансе токов реактивная индуктивная мощность равна реактивной емкостной мощности.

Это означает, что при резонансе токов, как и при резонансе напряжений (см. разд. 3.3), происходит обмен энергиями между энергией магнитного поля катушки индуктивности и энергией электрического поля конденсатора, но источник питания в этом обмене не участвует.

Полная реактивная мощность цепи при резонансе токов Q_рез, равная разности реактивной индуктивной Q_L и реактивной емкостной Q_C мощностей, равна нулю:

Q_рез = Q_L – Q_C = 0. (3.98)

Равенство нулю реактивной мощности Q_рез рассматриваемой цепи вытекает также из равенства нулю угла сдвига фаз между напряжением и током (j=0) в неразветвленной части цепи:

Q_рез= UIsinj = UIsin0˚ = 0. (3.99)

При этом реактивная индуктивная Q_L и реактивная емкостная Q_C мощности могут, как и реактивные токи (см. п. 4), приобретать большие значения, оставаясь равными друг другу.

Резонанс токов находит широкое применение в промышленных электрических установках (асинхронных двигателях, сварочных установках и др.) для повышения их коэффициента мощности (cosj). Повышение коэффициента мощности индуктивных потребителей электрической энергии обеспечивается параллельным подключением к ним батареи конденсаторов емкостью С. В этом случае реактивная емкостная мощность конденсаторной батареи Q_C уменьшает общую реактивную мощность установки Q, так как

Q =½Q_L – Q_C½, (3.100)

и, тем самым, увеличивает коэффициент мощности cosj, что приводит к уменьшению тока в проводах, соединяющих потребитель с источником электрической энергии [1,2,3].

На рис. 3.40 построена векторная диаграмма токов и напряжения для режима резонанса токов схемы цепи рис. 3.39.

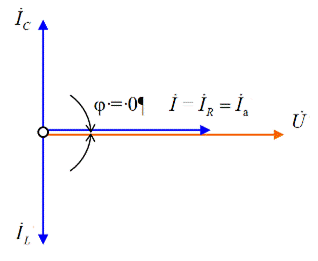
Рис. 3.40. Векторная диаграмма токов и напряжения для режима резонанса

токов при параллельном соединении R,L,C –элементов

При построении этой диаграммы необходимо учитывать характерные особенности режима резонанса токов: I = I_a , j = 0, I_L = I_C , т.е. ток в неразветвленной части цепи при резонансе токов равен активной составляющей тока I = I_P = I_a и имеет минимальное значение. Угол сдвига фаз между напряжением и током равен нулю: j = 0.

Отсюда следует, что вектор тока 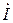совпадает по фазе с вектором напряжения .

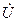Токи в параллельных ветвях с реактивными проводимостями B_L и B_C равны по модулю и противоположны по фазе:

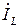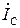½ ½=½- ½ (3.101)

и могут значительно превышать полный ток, т.е. ток в неразветвленной части цепи:

I_L = I_C >> I , если B_L = B_C >> G .

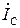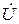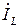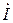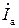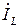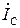Вектор тока опережает вектор напряжения на угол p/2 а вектор тока отстает от вектора напряжения на угол p/2. Вектор полного тока находят путем геометрического сложения векторов , и . При резонансе вектор полного тока совпадает по фазе с вектором напряжения 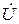(рис. 3.40).

Простейшей электрической цепью, в которой может наблюдаться в лабораторных условиях резонанс токов является цепь с параллельным соединением катушки индуктивности L_K и батареи конденсаторов емкостью С. Реальная катушка индуктивности обладает активным R_K сопротивлением провода и индуктивным сопротивлением X_L собственной индуктивности L. Поэтому рассматриваемую цепь синусоидального тока с двумя параллельными ветвями можно представить в виде схемы замещения, показанной на рис 3.41.

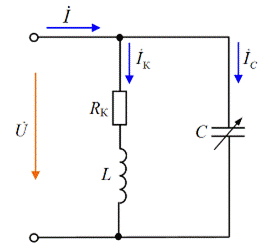
Рис. 3.41. Схема замещения с катушкой индуктивности

и конденсатором для исследования резонанса токов

Как было выше сказано, условием резонанса токов является равенство реактивных проводимостей ветвей цепи B_L = B_C. Реактивная индуктивная проводимость B_L катушки индуктивности с параметрами – R_K, X_L и реактивная емкостная проводимость В_С батареи конденсаторов определяются по формулам [2]:

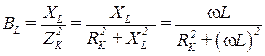; (3.102)

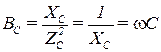. (3.103)

Приравнивая индуктивную и емкостную проводимости, условие резонанса токов можно записать в виде:

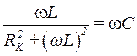, или 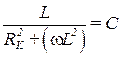, (3.104)

где w = w_рез – резонансная угловая частота.

Из этого выражения следует, что резонанс токов для цепи (рис. 3.41) можно получить, изменяя параметры R_K, L, C и w. В данной работе резонанс токов получается путем изменения емкости С батареи конденсаторов при постоянстве других параметров цепи.

Векторная диаграмма напряжения и токов для режима резонанса токов схемы рис. 3.41 построена на рис. 3.42.

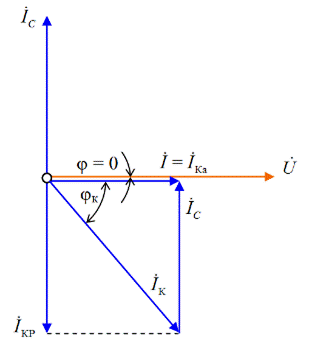
Рис. 3.42. Векторная диаграмма токов для цепи с катушкой индуктивности

и конденсатором в режиме резонанса токов

Так как при резонансе токов B_L = B_C , то реактивная составляющая тока 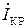ветви с катушкой индуктивности равна по модулю и противоположна по знаку реактивному емкостному току 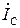ветви с конденсатором:

I_КР = -I_C.

Поэтому полный реактивный ток цепи в рассматриваемом случае равен нулю:

I_P = ½I_КР -I_C½= 0. (3.105)

Ток в неразветвленной части цепи (рис. 3.41), т.е. полный ток в цепи 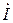при резонансе токов равен активной составляющей тока 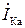и совпадает с ней по фазе (рис. 3.42):

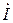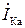= , (3.106)

а вектор тока 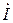на векторной токов (рис. 3.42) совпадает по направлению с вектором 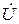входного напряжения.

Полная проводимость цепи синусоидального тока с параллельным соединением реальной катушки индуктивности и батареи конденсаторов (рис. 3.41) определяется по формуле:

Y = 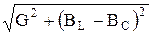. (3.107)

Причем из (3.103) видно, что реактивная емкостная проводимость В_С пропорциональна емкости С батареи конденсаторов.

Активная Р, реактивная Q и полная S мощности для цепи с параллельными ветвями определяются по формулам (3.108) − (3.110) и, с учетом особенностей схемы рис. 3.41, равны:

Р = Р_К = UIcosj = UI_Ка = R_К 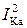= GU², (3.108)

Q = UIsinj = UI_КР = X 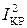= BU², (3.109)

S = UI = YU² = 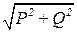. (3.110)

В режиме резонанса токов эти мощности будут равны:

Р_рез = UI = UI_Ка = R_К 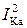= GU², (3.111)

Q_рез = 0, (3.112)

S_рез = Р_рез. (3.113)

Кривые, выражающие зависимость проводимостей, токов, мощностей и коэффициента мощности от емкости батареи конденсатора называются резонансными кривыми.

На рис. 3.43 приведены резонансные кривые (P, Q, S, I, cosj) = f(C), построенные в общем виде при U = const и w = 2pf = const.

Анализ этих зависимостей показывает, что при увеличении емкости батареи конденсаторов С полная мощность S сначала уменьшается, достигает минимума в режиме резонанса и становится равной активной мощности Р, а затем снова возрастает с увеличением емкости, в пределе стремясь к бесконечности.

Активная мощность Р_К, выделяемая на активном сопротивлении провода катушки индуктивности, не зависит от емкости конденсатора в другой ветви цепи и остается постоянной.

Реактивная мощность Q с увеличением емкости батареи конденсаторов снижается, становясь равной нулю в режиме резонанса, а затем возрастает.

Коэффициент мощности cosj изменяется с изменением емкости С в обратном порядке: сначала с увеличением емкости коэффициент мощности возрастает, достигая максимума равного единице в режиме резонанса, а затем уменьшается, в пределе стремясь к нулю.

Полная проводимость цепи Y (на рис. 3.43 не показана) , как и полная мощность S, сначала уменьшается, достигает минимума в режиме резонанса, а затем снова возрастает с увеличением емкости С, в пределе стремясь к бесконечности.

Ток в неразветвленной части цепи пропорционален полной проводимости
(I = YU). Поэтому характер его изменения подобен характеру изменения полной проводимости Y: сначала с ростом емкости конденсаторов ток I уменьшается, а затем снова начинает увеличиваться.

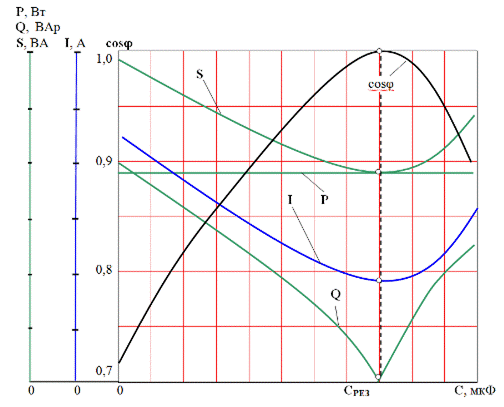
Рис. 3.43. Резонансные кривые P, Q, S, I, cosj в зависимости от емкости С при

параллельном соединении катушки индуктивности и батареи конденсаторов

Таким образом, резонансные кривые позволяют установить минимальную полную и реактивную мощность, и наименьший ток в неразветвленной части цепи при максимуме коэффициента мощности, равном единице, когда в цепи с параллельным соединением катушки индуктивности и батареи конденсаторов возникает резонанс токов.

Однако повышение коэффициента мощности выше 0,95 обычно не предусматривается, так как это связано со значительным увеличением емкости батареи конденсаторов.

Содержание работы

Лабораторная работа делится на четыре части:

1. Подготовительная часть.

2. Измерительная часть (проведение опытов и снятие показаний приборов).

3. Расчетная часть (определение расчетных величин по формулам).

4. Оформительская часть (построение векторных диаграмм).

Примечание

Электромонтажные работы по исследованию резонанса токов в цепи с параллельным соединением R,L,C-элементов на модернизированном лабораторном стенде ЭВ-4 не проводятся, в отличие от работ на старых стендах (см. в [2] – Работа 3а, п.2. Электромонтажная часть).

1.Подготовительная часть

Подготовка к проведению лабораторной работы включает:

1. Изучение теоретической части настоящего пособия и литературы [1,2,3,4], относящихся к теме данной работы.

2. Предварительное оформление лабораторной работы в соответствии с существующими требованиями [2,3].

В результате предварительного оформления лабораторной работы №3б в рабочей тетради или журнале студентом должен быть заполнен титульный лист, в работе должны быть указаны название работы и ее цель, приведены основные сведения по работе, взятые из раздела выше и формулы, необходимые для вычисления расчетных величин, представлены принципиальные и эквивалентные схемы замещения, заготовлены таблицы, соответственно числу опытов в работе.

Кроме этого, должно быть оставлено свободное место для построения векторных диаграмм.

2. Измерительная часть

Необходимые измерения параметров цепи однофазного тока с параллельным соединением электроприемников и исследования резонанса токов проводятся с помощью принципиальной схемы рис. 3.44. Данная схема соответствует панели модернизированног стенда ЭВ-4 [4] с аналогичной мнемосхемой и цифровыми (рис. 3.45)

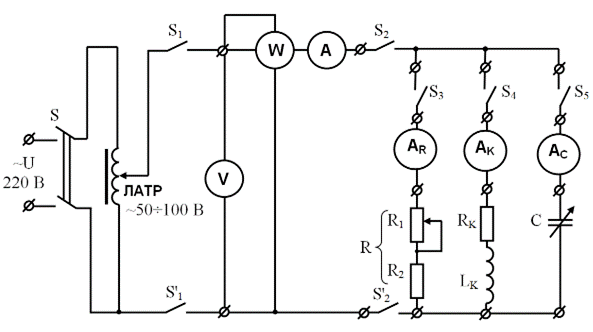
Рис. 3.44. Принципиальная схема цепи синусоидального тока

с параллельным соединением катушки индуктивности

и батареи конденсаторов для исследования резонанса токов

1. Перед подачей питания к исследуемой цепи на панели стенда с мнемосхемой и цифровыми измерительными приборами (рис. 3.45) перевести все выключатели (S₁ ÷ S₅, S'₁, S'₂), в нижнее положение (состояние – «откл»).

2. Подключить лабораторный автотрансформатор (ЛАТР), установленный на горизонтальной панели блока питания (рис. 3.46) к сетевому напряжению (~220 В), нажав черные кнопки «вкл» выключателей. При этом загораются две сигнальные лампы «сеть». После этого нужнообязательноповернуть ручку регулятора ЛАТРАа против часовой стрелки до упора, тем самым, снизив напряжение на его выходе до нуля.

Рис. 3.45. Паналь стенда с цифровыми измерительными приборами и
мнемосхемой для лабораторой работы 3а «Однофазная цепь
с параллельно соединенными электроприемниками.

3. Отключить батарею конденсаторов С нажатием соответствующей черной кнопки выключателя справа от конденсаторов на панели №4 стенда с мнемосхемой рис. 3.47.

4. Подать регулируемое напряжение от ЛАТРа ко входу исследуемой цепи и подключить цифровые измерительные приборы, установив на панели стенда с мнемосхемой кнопки выключателей (S₁ ÷ S₆, S'₁ ÷ S'₆) в положение «вкл» кроме выключателя S₃ (резистор R во всех опытах должен быть отключен). При этом должны засветиться зеленые цифры на электроизмерительных приборах.

5. Плавным поворотом по часовой стрелке ручки регулятора ЛАТРа (рис. 3.46) установить напряжение U на входе цепи порядка 50 ÷ 80 В, контролируя его цифровым вольтметром V (прибор ЩП02М, установленный слева на панели стенда – рис. 4.45). Следует поддерживать установленное напряжение постоянным во всех опытах с помощью ЛАТРа.

6. В процессе исследования цепи с параллельно соединенными катушкой индуктивности и батареей конденсаторов провести 7 опытов с различной емкостью батареи конденсаторов (величины емкостей для каждого опыта указаны в табл. 3.9) нажатием соответствующих кнопок выключателей на панели №4 стенда (рис. 3.47), постепенно увеличивая емкость с нуля до 120 мкФ. Перед подключением дополнительных конденсаторов в каждом опыте нужно обязательно отключить исследуемую цепь от источника питания (выхода ЛАТРа), переведя выключатели (S₁, S'₁) в нижнее положение «откл», а перед проведением замеров вновь подключить к напряжению питания цепь с помощью тех же выключателей.

7. Во всех опытах измерить входное напряжение U, потребляемую активную мощность Р и протекающий по цепи ток I, соответственно цифровыми измерительными приборами: вольтметром V, ваттметром W и амперметром А (см. принципиальную схему на рис. 3.44 и панель стенда на рис. 3.45).

8. Напряжение на батарее конденсаторов U_С и напряжение на катушке индуктивности U_К с параметрами R_K, L_K измерить цифровыми вольтметрами, соответственно V_C и V_K, установленными на панели стенда (рис. 3.45).

9. Полученные результаты измерений каждого опыта занести в табл. 3.9.

10. В конце измерительной части данной работы нужно отключить исследуемую цепь от источника питания и сам блок питания от силового щитка с помощью выключателей S₁ и S₁^' на панели с мнемосхемой (рис. 3.46). Сообщить преподавателю об окончании измерений и приступить к вычислениям параметров цепи.

Рис. 3.46. Панель блока питания лабораторного стенда

Рис. 3.47. Панель №4 стенда с мнемосхемами батареи конденсаторов
и катушки индуктивности