Результаты измерений и вычислений
Таблица № 3.9
| № опыта | С | Измерено | Вычислено | |||||||||||||
| U | P | I | IК | IС | RК | ZK | cosjK | IKa | IKP | Ia | IP | Q | S | cosj | ||
| мкФ | В | Вт | А | А | А | Ом | Ом | - | А | А | A | А | ВАр | ВА | - | |
| 1. | ||||||||||||||||
| 2. | ||||||||||||||||
| 3. | ||||||||||||||||
| 4. | ||||||||||||||||
| 5. | ||||||||||||||||
| 6. | ||||||||||||||||
| 7. |
Условия проведения опытов
Опыт 1: Конденсатор С отключен.
Опыты 2 −7: Различная емкость батареи конденсаторов (20 – 120 мкФ).
3. Расчетная часть
1. По результатам измерений вычислить величины полного сопротивления катушки индуктивности ZK, коэффициент мощности для ветви с катушкой cosjK , активную IKa и реактивную IKP составляющие тока катушки IK , активную Ia и реактивную IP составляющую полного тока цепи I, реактивную Q и полную S мощность, а также коэффициент мощности цепи cosj.
4.2. Вычисления параметров цепи проводить по формулам, приведенным в данном разделе выше. Рекомендуется для вычисления токов и коэффициентов мощностей использовать известные формулы, выражающие соотношения сторон и углов в прямоугольных треугольниках, образованных на векторной диаграмме токов рис. 3.42.
4. Оформительская часть – построение векторной диаграммы
и резонансных кривых
1. Перед построением векторной диаграммы внимательно изучить правила их построения, изложенные в разделе 1.4, а также общую часть разделов 3.1, 3.4, 3.5. Выбрать масштабы для напряжения mU и токов mI , как указано в разделе 1.4.
2. С помощью выбранных масштабов определить длины вектора напряжения и токов. Занести выбранные масштабы, измеренные и вычисленные величины напряжения и токов и длины векторов этих величин для опыта, соответствующего резонансу токов в табл. 3.10.
3. Построить для случая резонанса токов векторную диаграмму токов и напряжения.
Масштабы, величины и длины векторов напряжения и тока
Таблица № 3.10
| № опыта | Масштабы | Базовый вектор | Остальные векторы | |||||||||||
| mU | mI | U | IKa | lIKa | IKP | lIKp | IK | lIK | IC | lIC | I | lI | ||
| В/см | А/см | B | см | А | см | А | см | А | см | А | см | А | см | |
| 1. |
4. По данным табл. 3.9 построить в выбранных масштабах, как показано на рис. 3.43 в общем виде, резонансные кривые P, Q, S, I, cosj в зависимости от емкости С (0 ÷ 120 мкФ) при параллельном соединении катушки индуктивности и батареи конденсаторов.
Работа 4 Цепь трехфазного тока при соединении электроприемников звездой
· Цель работы
Исследование цепи трехфазного синусоидального тока при соединении активных электроприемников звездой к трех- и четырехпроводной сети.
Общие сведения
Трехфазной электрической цепью называется совокупность трех электрических цепей переменного тока с синусоидальными ЭДС одной и той же частоты, сдвинутыми по фазе относительно друг друга на угол j = 2p/3 = 120° и генерируемые в одном источнике электрической энергии.
Каждую из частей трехфазной системы, характеризующуюся одинаковым током, называют фазой. Таким образом, понятие фаза в электротехнике имеет два значения: первое – аргумент синусоидально изменяющейся величины, второе значение − часть одно-, трех-, или в общем случае, многофазной системы электрических цепей. В электрических машинах под фазой также подразумевают одну из идентичных m-фазных обмоток статора или ротора (где m − общее число фаз).
Фазы трехфазной цепи принято обозначать первыми буквами латинского алфавита: А, В, С–при соединении фаз звездой и двойными буквами АВ, ВС, СА – для схемы соединения фаз треугольником [1,2]. Индексы фазных величин имеют те же буквы.
Источником энергии в трехфазной системе служат трехфазные синхронные генераторы, установленные на всех крупных электростанциях [1]. Простейший двухполюсный синхронный генератор (рис. 3.48) имеет на статоре три одинаковые обмотки, сдвинутые на угол 120° относительно друг друга. При вращении ротора, выполненного в виде электромагнита (обмотка возбуждения ротора, не показанная на рисунке, включена в цепь постоянного тока) в фазах-обмотках статора индуцируются три синусоидальные ЭДС еА, еВ, еС одинаковой частоты и с равными амплитудами Em, сдвинутыми по фазе относительно друг друга на угол 2p/3 (или 120о), как показано на рис. 3.49,а.
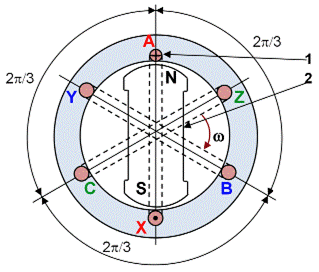
Рис. 3.48. Упрощенная конструкция трехфазного генератора
1– статор с трехфазной обмоткой А-Х, В-У, С-Z;
2 – двухполюсный ротор (полюса N-S создаются постоянным током в обмотке
возбуждения ротора, не показанной на рисунке)
Если для фазы А начальную фазу ЭДС еА принять равной нулю, то мгновенные значения ЭДС всех трех фаз равны:
еА = Еmsinwt;
eB = Emsin(wt – 2p/3); (3.114)
eC = Emsin(wt + 2p/3).
Комплексные значения ЭДС трехфазного симметричного генератора можно выразить через одинаковое для всех трех фаз действующее значение ЭДС Е и соответствующий комплексный множитель:
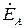= Е еj0˚ = E(1 + j0);
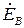= Е е-j2p/3 = E ( 
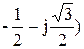; (3.115)
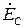= Е е+j2p/3 = E 
.
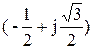Комплексная величина е+j2p/3 = 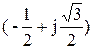называется фазным множителемтрехфазной системы и обозначается буквой а. Умножение комплексной величины на фазный множитель асоответствует повороту изображающего вектора на угол 2p/3 = 120о в положительном направлении, т.е. против движения часовой стрелки.
Таким образом:
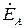= ЕФ ; 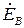= ЕФа2 ; 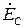= ЕФа. (3.116)
Так как комплексному числу соответствует вектор на комплексной плоскости (см. разд. 1.3), то трехфазная система ЭДС может быть изображена в виде трех равных по величине векторов 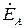, , 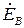, 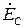сдвинутых на фазовый угол ±2p/3 относительно друг друга, как показано на рис. 3.49,б. Такие векторы называются трехфазными симметричными векторами.
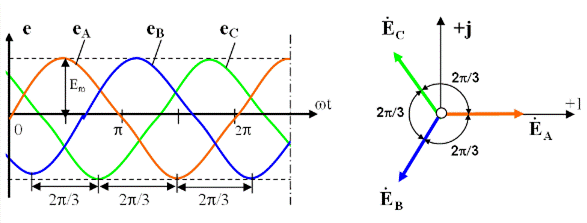
а) б)
Рис. 3.49. Трехфазная система ЭДС
а) – график мгновенных значений трехфазной системы ЭДС;
б) – векторная диаграмма трехфазной системы ЭДС.
Существуют две основные схемы соединения фаз обмоток генератора и трехфазных электроприемников, а именно, схема соединения звездой с условным обозначением «Y» и схема соединения треугольником с условным обозначением «D».
При соединении фаз А, В, С звездой концы фаз обмоток генератора или электроприемников объединяют в общий узел, который называют нейтралью или нейтральной точкой и обозначают буквой «N».
Нейтральные точки трехфазного источника и трехфазного электроприемника соединены проводом, который называют нейтральным проводом. Нейтральный провод часто соединяют с землей и тогда его принято называть нулевым.
Три провода, соединяющие фазы трехфазного источника и электроприемника называются линейными проводами, которые обозначают теми же буквами А, В, С, что и одноименные фазы.
Эквивалентная схема замещения трехфазной цепи при схеме соединения звездой представлена на рис. 3.50.
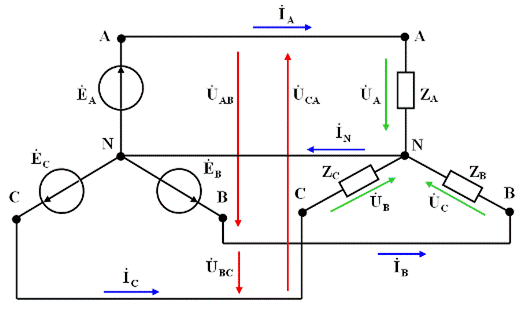
Рис. 3.50. Схема замещения цепи трехфазного тока при соединении
фаз источника (стрехфазного генератора) и электроприемников звездой.
Из схемы замещения на рис. 3.50 видно, что токи в линиях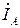 
, 
, 
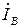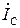являются теми же токами в одноименных фазах источников и электроприемников. Таким образом, для трехфазной цепи при соединении фаз звездой линейные токи (в общем виде обозначаемые IЛ) равны одноименным фазным токам IФ
IЛ = IФ. (3.117)
Для трехфазной схемы соединения источников и электроприемников (рис. 3.50) на основании второго закона Кирхгофа [1], если пренебречь активным сопротивлением линейных и нейтрального проводов, можно считать, что фазные ЭДСисточников равны одноименным фазным напряжениям:
= 
; = 
; = 
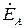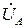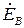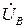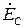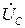. (3.118)
Из закона Ома можно определить соотношение между фазными токами, напряжениями и сопротивлениями:
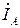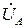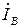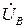= /ZА ; = /ZB ; 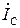= 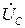/ZС, (3.119)
где ZА, ZB , ZС – комплексные сопротивления электроприемников (трехфазной нагрузки).
Для активной нагрузки фаз линейные или фазные токи равны:
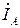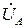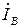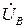= /RA; = /RВ; 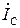= 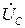/RС. (3.120)
Из выражений (3.120) видно, что для случая активной нагрузки фаз одноименные фазные напряжения и токи совпадают по фазе (j = 0).
Из первого закона Кирхгофа [1] следует, что:
+ + = 
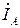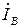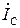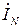, (3.121)
т.е. ток в нейтральном проводе равен сумме комплексных фазных (линейных) токов или в геометрическом представлении – геометрической сумме векторов этих токов.
Помимо трех фазных напряжений при схеме соединения звездой, как видно из рис. 3.50, имеются три напряжения между тремя парами линий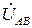 
, 
, 
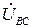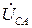, которые называются линейными напряжениями.
На основании второго закона Кирхгофа [1] из выражений (3.118) для схемы на рис. 3.50 можно получить соотношения между фазными ЭДС и линейными напряжениями:
– = ;
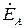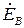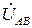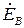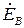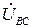– = ; (3.122)
– = . .
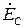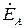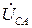Анализ этих выражений показывает, что для симметричной системы ЭДС линейные напряжения также будут симметричными, т.е. одинаковы по величине и сдвинуты относительно друг друга на один и тот же угол 2p/3 = 120о.
Соотношения между линейными и фазными напряжениями для схемы соединения звездой по второму закону Кирхгофа имеют вид, аналогичный формулам (3.122):
= – ;
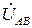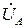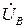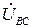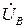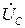= – ; (3.123)
= – .
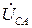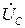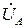Если сопротивления фаз имеют одинаковый характер и равны по величине:
ZА =ZB =ZС =ZФ =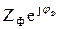 
, (3.124)
то такую нагрузку называют симметричной. Для симметричной активной нагрузки:
ZФ = RA = RB = RC = RФ . (3.125)
Из выражения (3.115) видно, что симметричная трехфазная система комплексных ЭДС в сумме образует ноль:
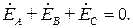(3.126)
Это означает, что для любого момента времени алгебраическая сумма мгновенных значений этих ЭДС (рис. 3.49,а), как и их векторная сумма (рис. 3.49,б) также равны нулю:
еА + еВ + еС = 0. (3.127)
Из соотношений (3.118) следует, что сумма комплексных симметричных линейных напряжений также равна нулю:
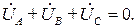(3.128)
Для симметричной трехфазной нагрузки, определяемой соотношениями (3.120), (3.121), следует, что фазные (линейные) токи также будут симметричными, т.е. одинаковы по величине и сдвинутыми относительно друг друга на один и тот же угол 2p/3 = 120°.
Сумма симметричных комплексных токов аналогично формулам (3.126) и (3.128) также равна нулю:
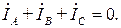
Сопоставление выражений (3.121) и (3.129) показывает, что для симметричной нагрузки фаз, соединенных звездой ток в нейтральном проводе всегда равен нулю
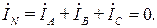(3.129)
Если нагрузка фаз трехфазного электротехнического устройства по своей конструкции всегда симметричная, как например, в трехфазных асинхронных двигателях (где три симметричные фазы-обмотки статора имеют одинаковые сопротивления), то для их соединения по схеме звезда к трехфазной сети нейтральный провод никогда не присоединяется к нейтральной точке «N» фазных обмоток статора. [1,2].
Примечание. В то же время заземленный (нулевой) нейтральный провод используется в целях электробезопасности за счет его присоединения к корпусу асинхронного двигателя [1,4].
На рис. 3.51 показана векторная диаграмма напряжений и токов для трехфазной симметричной активной нагрузки, соединенной звездой, которая построена на основании формул (3.120), (3.123), (3.128), (3.129) по правилам построения векторных диаграмм (см. разд. 1.4 и Приложение 4).
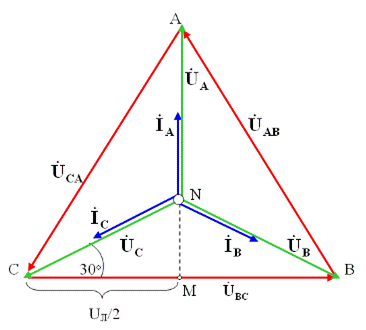
Рис. 3.51. Векторная диаграмма напряжений и токов для трехфазной симметричной активной нагрузки соединенной звездой
Из векторной диаграммы на рис. 3.51 видно, что в прямоугольном треугольнике CNM отношение катета СМ, равного половине линейного напряжения UЛ/2 к гипотенузе CN, соответствующей фазному напряжению UФ (т.к.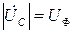 
) определяется по формуле:
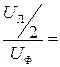cos30о = 
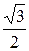. (3.130)
Из этого выражения следует, что
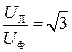»1,73, (3.131)
т.е. для симметричной нагрузки фаз соединенных звездой линейные напряжения больше фазных в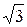 
» 1,73 раз.
Таким образом, если линейные напряжения в трехфазной сети равны 380 В, то фазные напряжения для трехфазной нагрузки соединенной звездой будут в 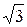раз меньше и равны 220 В. Напряжения 220/380 В являются стандартными величинами фазных и линейных напряжений в низковольтных сетях промышленной частоты 50 Гц в нашей стране и в других европейских странах.
Рассмотри случай несимметричной нагрузки фаз соединенных звездой с нейтральным проводом. Трехфазная нагрузка будет несимметричной при неравном сопротивлении фаз. Для примера предположим, что для несимметричной активной нагрузки фаз:
RA < RB = RC. (3.132)
В этом случае, при условии симметричной трехфазной системы ЭДС (3.114), (3.115), по-прежнему остаются справедливыми равенства (3.118)–(3.123) и (3.126)–(3.128). В частности, на основании соотношений (3.118) фазные напряжения 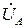, , 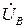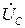остаются теми же (симметричными), что и для симметричной нагрузки фаз. Но по закону Ома становятся неравными фазные токи, обратно пропорциональные сопротивлениям электроприемников:
IA = UA/RA > (IB = UB/RB) = (IC = UC/RC). (3.133)
Для активной несимметричной нагрузки (3.132) эти токи, исходя из выражений (3.120), также будут совпадать по фазе с одноименными фазными напряжениями, как и для симметричной активной нагрузки.
Таким образом, векторная диаграмма напряжений для несимметричной нагрузки фаз останется неизменной, по сравнению со случаем симметричной нагрузки
Неравенство фазных токов для несимметричной нагрузки (IA > IB = IC)приведет к появлению тока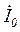 
в нейтральном проводе:
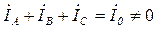
Векторная диаграмма напряжений и токов для данного случая несимметрии активной нагрузки фаз (RA < RB = RC) будет выглядеть, как изображено на рис 3.52.
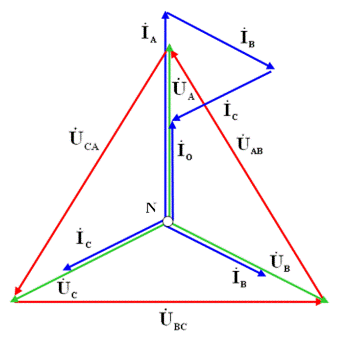
Рис. 3.52. Векторная диаграмма напряжений и токов при соединении фаз звездой
с нейтральным проводом при несимметричной нагрузке
для случая RA < RB = RC
Рассмотри тот же случай несимметричной нагрузки (3.132), но при отсутствии нейтрального провода.
При этом остается симметрия фазных ЭДС, определяемая (3.114), (3.115) и, следовательно, исходя из формул (3.122) – симметрия линейных напряжений 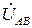, , 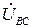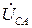. Соотношения между линейными и фазными напряжениями на основании второго закона Кирхгофа по-прежнему определяются выражениями (3.123). Однако, из-за отсутствия нейтрального провода фазные напряжения, (как и фазные токи) при несимметричной активной нагрузке (3.132) также становятся несимметричными, т.е. неравными по величине с неодинаковыми фазовыми углами, определяемыми на основании закона Ома:
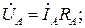
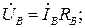(3.134)
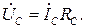
В качестве примера, на рис. 3.53 показана векторная диаграмма токов и напряжений для несимметричной активной нагрузки фаз без нейтрального провода.
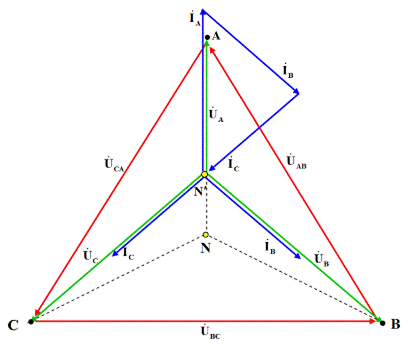
Рис. 3.53. Векторная диаграмма токов и напряжений при несимметричной
активной нагрузки фаз соединенной звездой
при отсутствии нейтрального провода для случая RA < RB = RC
Из векторной диаграммы видно, что в случае несимметричной активной нагрузки фаз, определяемой соотношениями (3.132), при отсутствии нейтрального провода:
1. Линейные напряжения 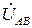, , 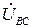, 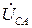оставаясь симметричными, т.е. одинаковыми по величине и сдвинутыми по фазе на 120о, по-прежнему образуют замкнутый равносторонний треугольник напряжений, как и на векторной диаграмме рис. 3.51;
2. Отсутствие нейтрального провода приводит к невозможности возникновения тока в нем ( 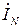=0). Это, в свою очередь, для несимметричной нагрузки вызывает перераспределение фазных токов так, чтобы их комплексная сумма на основании первого закона Кирхгофа также была равна нулю:
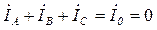. (3.135)
На векторной диаграмме рис. 3.53 равенство (3.135) показано в виде замкнутого треугольника цепочки векторов 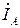, , 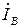, 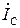из чего следует равенство нулю геометрической суммы этих векторов (см. Приложение 4);
3. При заданных несимметричных нагрузках фаз (3.132) фазные токи на основании закона Ома могут изменяться только за счет изменения фазных напряжений, определяемых соотношениями (3.134).
Следовательно, обрыв нейтрального провода при несимметричной нагрузке фаз приводит к изменению фазных напряжений, т.е. фазные напряжения также становятся несимметричными.
На векторной диаграмме рис. 3.53 видно, что при неравенстве фазных нагрузок фазные напряжения также становятся неравными по величине:
UA < UB = UC . (3.136)
4. С другой стороны, соотношения (3.123) для несимметричной нагрузки по-прежнему остаются справедливыми. Поэтому на векторной диаграмме рис. 3.53 начала векторов фаз также сведены в общую точку N*, называемую нейтралью[1], а концы этих векторов совпадают с вершинами равностороннего треугольника АВС, как и на векторной диаграмме рис. 3.51. Сама нейтраль N* переместиться из центра тяжести равностороннего треугольника линейных напряжений N в сторону вершины треугольника со сравнительно бóльшей одноименной фазной нагрузкой, т.е. с меньшим фазным сопротивлением (в данном случае, в сторону вершины А).
Рассмотрим аварийный режим несимметричной активной нагрузки соединенной звездой – короткое замыкание одной из фаз при отсутствии (обрыве) нейтрального провода. На рис. 3.54 изображена трехпроводная цепь с коротким замыканием фазы А:
RA = 0; RB = RC = RФ ,
а на рис. 3.55 представлена векторная диаграмма напряжений и токов для этого режима.
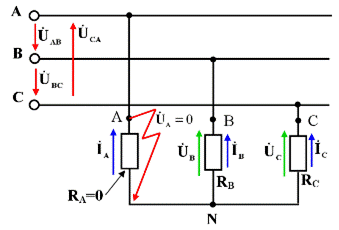
Рис.3.54. Схема включения трехфазной нагрузки, соединенной звездой
в трехпроводную сеть с коротким замыканием фазы «А»
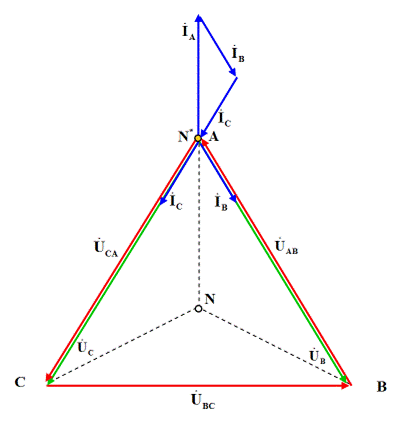
Рис. 3.55. Векторная диаграмма для режима короткого замыкания фазы «А»
для схемы нагрузки, соединенной звездой без нейтрального провода
Как видно из векторной диаграммы рис. 3.55 для этого режима, общая точка начала трех векторов фазных напряжений – нейтраль N переместится к вершине А равностороннего треугольника линейных напряжений АВС. Следовательно, фазное напряжение 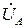уменьшится до нуля, а два других фазных напряжения увеличатся до величины линейных напряжений:
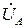= 0; = - ; = .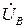
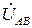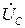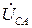UA = 0; UВ = UC = UЛ;
Пропорционально напряжениям UA и UB (по закону Ома) увеличатся и фазные токи IA и IB , совпадая с ними по фазе: IA = IB = UЛ/RФ .
В короткозамкнутой фазе А ток IA определяется на основании первого закона Кирхгофа и формулы 3.135: = -( + ).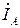
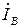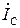На векторной диаграмме рис. 3.55 это подтверждается направлением векторов в замкнутом треугольнике векторов токов , , .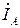
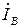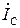Рассмотрим еще один аварийный режим несимметричной активной нагрузки соединенной звездой – отключение (обрыв) одной из фаз при отсутствии (обрыве) нейтрального провода. На рис. 3.56 изображена трехпроводная цепь с отключенной фазой А при условии: RA = ¥; RB = RC = RФ , а на рис. 3.57 представлена векторная диаграмма напряжений и токов для этого режима.
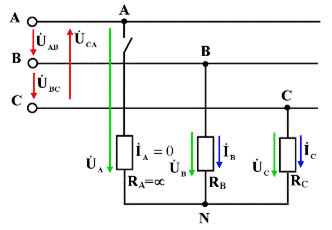
Рис. 3.56. Режим несимметричной нагрузки – отключение фазы «А»
для трехфазной активной нагрузки соединенной звездой
без нейтрального провода
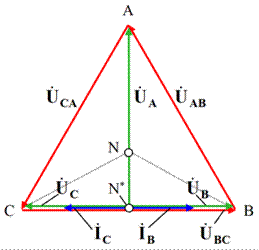
Рис. 3.57. Векторная диаграмма для трехфазной активной нагрузки соединенной звездой
при отключении фазы «А» и при отсутствии нейтрального провода
Из векторной диаграммы на рис. 3.57 видно, что при симметричной системе линейных напряжений 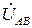, , 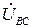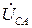в случае отключении фазы А и отсутствии нейтрального провода общая точка начала векторов фазных напряжений – нейтраль N переместится вниз на середину нижней стороны ВС равностороннего треугольника АВС. При этом напряжение фазы А увеличится, а двух других фаз уменьшится до величин: UA= UЛ sin60о = UЛ 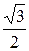» 0,87UЛ, UB = UC = UЛ/2.
Ток в фазе А, из-за ее отключения отсутствует (IA = 0), а в фазах В и С, соединенных последовательно и подключенных к линейному напряжению 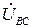будет протекать один и тот же ток 
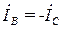(см. рис. 3.56 и рис. 3.57), по величине определяемый законом Ома:
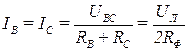. (3.137)
Анализ приведенных в настоящем разделе формул и векторных диаграмм позволяет понять назначение нейтрального провода: случаи, когда он необходим и когда он не требуется, а также последствия, к которым может привести его отсутствие (обрыв нейтрального провода).
Нейтральный провод в трехфазной четырехпроводной сети служит для выравнивания фазных напряжений при несимметричной нагрузки фаз соединенных звездой,а также для протекания по нему в этом режиме уравнительного тока .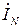
Это определение назначения нейтрального провода выявляет два обстоятельства:
Во-первых, что выполняет нейтральный провод – выравнивает фазные напряжения (делает их симметричными т.е. одинаковыми по величине, сдвинутыми на один и тот же фазовый угол). Во-вторых, когда используется нейтральный провод – когда нагрузка фаз несимметричная, т.е. неодинаковая по величине и однородности в разных фазах.
Нейтральный провод не присоединяется к нейтрали фаз соединенных звездой для заведомо симметричной трехфазной нагрузки (например – трехфазные асинхронные двигатели).
Это объясняется тем обстоятельством, что для симметричной нагрузки ток в нейтральном проводе отсутствует (3.129), поэтому нейтральный провод и не подсоединяется к общей точке фаз (нейтрали N), соединенных звездой.
В то же время, заземленный (нулевой) нейтральный провод используется в целях электробезопасности, за счет его присоединения к металлическому корпусу трехфазной симметричной нагрузки, например к корпусу трехфазного асинхронного двигателя.
Общую активную Р, реактивную Q и полную S мощности электроприемников в трехфазной цепи при их соединении звездой можно при любой несимметрии вычислить как арифметические суммы этих мощностей для отдельных фаз:
Р =РА+ РВ+ РС; (3.138)
Q =QA+QB+QC; (3.139)
S =SA+ SB+ SC =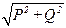 
, (3.140)
где мощности P, Q, S для отдельной фазы вычисляются по формулам (3.20)–(3.24), приведенным в разделе 3.2.
Для симметричной трехфазной нагрузки мощности вычисляются для одной фазы, а затем утраиваются:
Р = 3РФ; Q = 3QФ ; S = 3SФ. (3.141)
Для симметричной трехфазной нагрузки мощности P, Q, S можно вычислить через линейные напряжения UЛ и токи IЛ по формулам:
Р =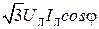 
; (3.142)
Q =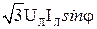 
; (3.143)
S =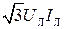 
. (3.144)
Содержание работы
Лабораторная работа 4 делится на четыре части:
1. Подготовительная часть.
2. Измерительная часть (проведение опытов и снятие показаний приборов).
3. Расчетная часть (определение расчетных величин по формулам).
4. Оформительская часть (построение векторных диаграмм).
1. Подготовительная часть
Подготовка к проведению лабораторной работы включает:
1. Изучение теоретической части настоящего пособия и литературы [1,2,3,4], относящихся к теме данной работы.
2. Предварительное оформление лабораторной работы в соответствии с существующими требованиями [2,3].
В результате предварительного оформления лабораторной работы №4 в рабочей тетради или журнале (на листах формата А4 с компьютерной распечаткой) студентом должен быть заполнен титульный лист, в работе должны быть указаны название работы и ее цель, приведены основные сведения по работе, взятые из раздела выше и формулы, необходимые для вычисления расчетных величин, представлены принципиальные и эквивалентные схемы замещения, заготовлены таблицы, соответственно числу опытов в работе.
Кроме этого, должно быть оставлено свободное место для построения трех векторных диаграмм.
2. Измерительная часть
Необходимые измерения параметров исследуемой цепи трехфазного синусоидального тока при соединении активных электроприемников звездой к трех- и четырехпроводной сети проводятся с помощью принципиальной схемы (рис. 3.58). Данная схема соответствует панели модернизированног стенда ЭВ-4 [4] с аналогичной мнемосхемой и цифровыми измерительными приборами (см. фото на рис. 3.60). Этой схеме соответствует схема замещения, показанная на рис. 3.59.
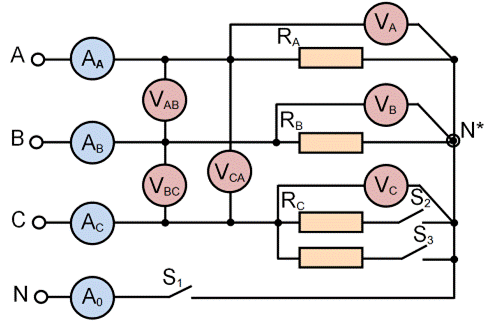
Рис. 3.58. Принципиальная схема соединения электроприемников звездой
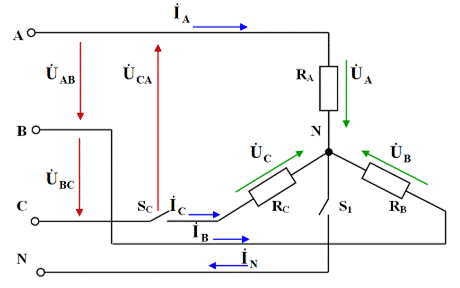
Рис. 3.59. Эквивалентная схема замещения соединения электроприемников звездой
Рис. 3.60. Паналь стенда с цифровыми измерительными приборами и
мнемосхемой для проведения лабораторой работы №4
«Цепь трехфазного тока при соединении электроприемников звездой»
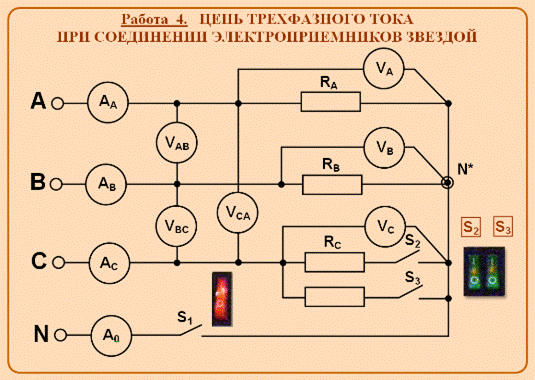
Рис. 3.61. Мнемосхема для лабораторой работы 4
«Цепь трехфазного тока присоединении электроприемников звездой»
В процессе проведения измерений для данной лабораторной работы следует провести следующие действия:
Подключить блок питания к трехфазному сетевому напряжению (~3´220 В) нажатием на стенде кнопки «вкл» трехполюсного выключателя S. При этом рядом с выключателем должна загореться сигнальная лампа .
В процессе исследования трехфазной цепи провести шесть опытов. Полученные результаты измерений каждого опыта занести в таблицу 3.11. Условия проведения опытов указаны рядом с этой таблицей.
В первом опыте установить режим трехфазной симметричной нагрузки
(RА = RВ = RС) с нейтральным проводом, переведя выключатель S2 в положение «вкл», а выключатель S3 в положение «откл». Нейтральный провод включить с помощью выключателя S1 (см. рис. 3.61).
Во втором опыте с той же трехфазной симметричной нагрузкой без нейтрального провода отключить от нее нейтральный провод N выключателем S1 Убедится, что по сравнению с первым опытом показания всех включенных приборов не меняются.
В третьем опытенесимметричной трехфазной нагрузкис нейтральным проводом к трехфазной нагрузке опять подключить нейтральный провод N выключателем S1. Установить несимметричный режим (RС < RА = RВ), уменьшив сопротивление в фазе «С», за счет параллельного соединения двух одинаковых сопротивлений RС с помощью выключателей S2 и S3 (см. рис. 3.61). Убедится, что при неизменных фазных напряжениях, фазный ток IC увеличился в 2 раза, а в двух других фазах фазные токи остались прежними.
В четвертом опытенесимметричной трехфазной нагрузкибез нейтрального провода при установленной в предыдущем опыте несимметричной нагрузке отключить выключателем S1 нейтральный провод N. Пронаблюдать, как при этом меняются фазные напряжения и фазные токи.
В пятом опытенесимметричной трехфазной нагрузки без нейтрального провода с отключением одной фазы в режиме с отключенным нейтральным проводом N провести отключение нагрузки фазы «С» с помощью выключателей S2 и S3 (см. рис. 3.61). Проследить, как в этом опыте изменятся фазные напряжения и фазные токи.
В шестом опытенесимметричной трехфазной нагрузки без нейтрального провода с коротким замыканием одной фазы при отключении нейтрального провода N (выключатель S1 разомкнут) и одинаковых сопротивлениях в фазах «В» и «С» (выключатель S2 замкнут, а – S3 разомкнут) провести короткое замыкание в фазе А дополнительным выключателем S4 (на схеме рис. 3.61 не показано)
Дата добавления: 2016-04-11; просмотров: 3000;