На него последовательности радиоимпульсов.

Процессы в контуре. Колебания, которые возникнут в контуре под влиянием радиоимпульса, будут такими же, как и при включении непрерывного колебания (см. раздел 4.4). При ω_р≠ω_о в контуре возникнут биения с частотой 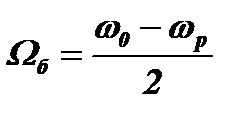. Однако биения будут существовать в контуре только в течение длительности импульса τ. К моменту окончания импульса амплитуда биений U_б(τ) в контуре будет равна:

.

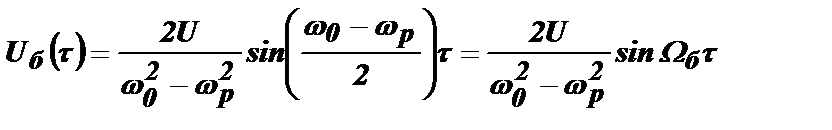Характер колебаний, которые останутся в контуре после окончания импульса, будет зависеть от соотношения между его длительностью τ и периодом биений 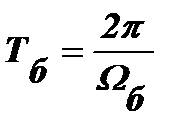. Если длительность импульса τ₁ (рис. 4.42, а)равнацелому числу полупериодов биений: 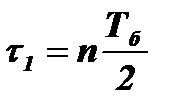(n=1,2,3…), то колебания в контуре после окончания импульса будут отсутствовать. Если же на длительности импульса τ₂ (рис. 4.42, б) укладывается целое число нечетных четвертей периодов биений: 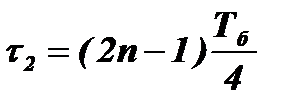, то в момент окончания импульса биения будут иметь максимальную амплитуду U_б(τ), а после его окончания в контуре останутся и будут длительно существовать свободные колебания с частотой ω_о. Очевидно, что между этими двумя крайними случаями возмож­ны любые промежуточные соотношения τ и Т_б.

При ω_р=ω₀ амплитуда колебаний в контуре будет непрерывно расти в течение длительности импульса τ₃ (рис. 4.42, в) до значения U_б(τ)=Uτ/2ω_p (см. раздел 4.4), после чего в контуре будут длительно существовать свободные колебания с частотой ω_о. Очевидно, что параметры (амплитуда и фаза) этих свободных колебаний, определяющих условия возникновения резонанса в контуре, зависят от параметров вызывающих их биений.

Различие между воздействием на контур видеоимпульсов и радиоимпульсов. Процессы, возникающие в контуре при воздействии на него коротких видеоимпульсов и коротких радиоимпульсов, существенно различаются. В первом случае фазовый сдвиг между свободными колебаниями, вызванными соседними видеоимпульсами, зависит только от периода их повторения. Во втором случае в контуре возникают биения и фазовый сдвиг между свободными колебаниями, вызванными соседними радиоимпульсами, начинает зависеть не только от периода их повторения, но и от фазы биений в момент окончания радиоимпульса. В результате механизмы возникновения накопительного резонанса в контуре в этих двух случаях будут различными.

Переворот фазы биений. Перед исследованием резонанса в колебательном контуре, на который воздействует последовательности радиоимпульсов, рассмотрим одну из особенностей процесса биений – сложения двух колебаний с одинаковыми амплитудами и разными частотами. Эта особенность заключается в скачке фазы высокочастотного заполнения биений на 180° после каждого полупериода Т_δ. Именно эта особенность отличает биения от амплитудно-модулированного колебания, фаза которого не имеет разрывов, даже в том случае, когда при 100%-ной модуляции амплитуда колебаний уменьшается до нуля.

Для пояснения указанного скачка фазы используем векторную диаграмму суммы двух колебаний с близкими частотами ω_о и ω_р (рис. 4.43).

Обозначим вектор колебания, имеющего частоту ω_о, через 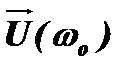и сделаем его неподвижным (для этого представим себе, что рисунок вращается с той же частотой ω_о в обратную сторону). Тогда вектор колебания, имеющего частоту ω_р – 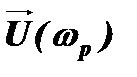, будет медленно вращаться вокруг вектора 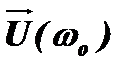с разностной частотой 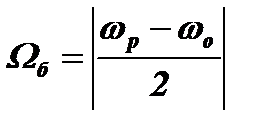. Из диаграммы видно, как величина суммарного вектора 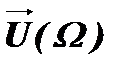, равная амплитуде биений, меняется от удвоенной амплитуды U_δ одиночного колебания U, до нуля. Из векторных диаграмм также видно, как при переходе амплитуды суммарного вектора 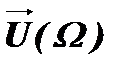через нуль его фаза, которая является фазой биений, скачком переворачивается на 180°.

Возникновение резонанса. Будем постепенно изменять частоту контура f_o, наблюдая за сигналом на его выходе. Также как и при воздействии на контур последовательности видеоимпульсов, резонанс в этом случае возникнет тогда, когда свободные колебания, оставшиеся в контуре после воздействия отдельных радиоимпульсов, будут складываться синфазно. Для этого необходимо, чтобы разность фаз между любой парой этих свободных колебаний (в простейшем случае между колебаниями, оставшимися после двух соседних импульсов) была равна ∆φ=2πm, где m=0, ±1, ±2, ... .

На рисунке 4.44 показаны два соседних радиоимпульса последовательности, а ниже - колебания, возникающие в контуре под действием каждого из этих им­пульсов. Моменты времени τ₁ и τ₂ означают окончания первого и второго импульсов, а моменты Т₁ и Т₂ – окончания первого и второго периодов. Рассмотрим, от чего зависит разность фаз ∆φ между свободными колебаниями, оставшимися в контуре после окончания обоих импульсов в момент времени Т₂, соответствующий началу третьего импульса.

Определение разности фаз. Эта разность фаз будет определяться двумя причинами.

Первой причиной является начальная фаза колебаний, возникающих в контуре с приходом каждого импульса. Для первого импульса это - фаза, с которой он начнется в момент t=0 (обозначим эту фазу как 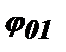), а для второго импульса это - фаза, с которой он начнется в момент T₁ (обозначим эту фазу как ).

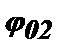Второй причиной является набег фазы колебаний в контуре за интервал времени от момента возникновения импульса (0 – для первого импульса и Т₁ – для второго импульса) до момента Т₂. Этот интервал времени делится на два периода. В первом периоде этого интервала в контуре существуют биения с частотой заполнения 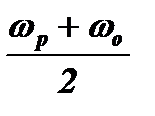. Набег фазы за этот период будет равен 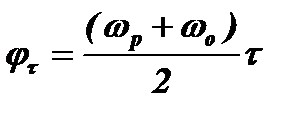. Этот период продолжается от 0 до τ₁ для первого импульса и от Т₁ до τ₂ для второго импульса. Во втором периоде этого интервала в контуре останутся только свободные колебания, имеющие частоту ω_о. Этот период продолжается от τ₁ до Т₂ для первого импульса и от τ₂ до Т₂ для второго импульса. Набег фазы в этот период будет равен, соответственно для первого и второго импульсов, 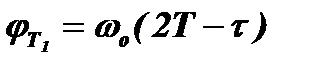и 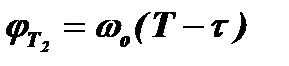. Таким образом, общий набег фазы за весь интервал времени от момента возникновения колебания до момента Т₂ будет равен для первого импульса 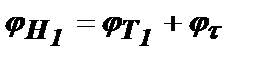и для второго импульса .

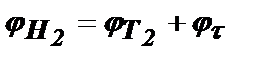В момент Т₂ результирующая фаза колебания, вызванного в контуре первым импульсом, будет равна 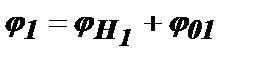, а результирующая фаза колебания, вызванного в контуре вторым импульсом, будет равна 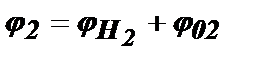. Для синфазного сложения колебаний в момент Т₂ необходимо, чтобы выполнялось равенство Δj = j₁ – j₂ = 2pm, где (m=0,±1,±2,...). Тогда:

.

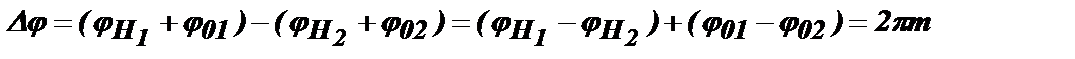Рассмотрим сначала первое слагаемое 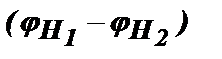, входящее в выражение для ∆j. Подставляя сюда значения 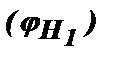и 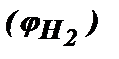, получим:

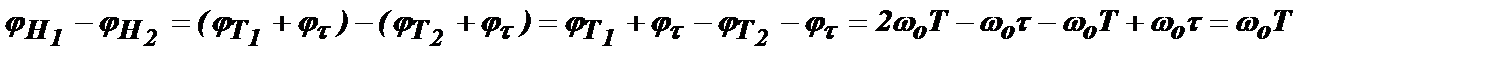
Таким образом, эта разность фаз не зависит от длительности радиоимпульса τ и может быть использована при анализе любого радиоимпульсного процесса.

Второе слагаемое (j₀₁–j₀₂) рассмотрим для случая, когда импульсы последовательности вырезаются из непрерывного колебания с частотой ω_р и начальная фаза каждого импульса определяется этим колебанием. Разность начальных фаз n-го и (n+1)-го импульсов из фрагмента последовательности, представленного на рис. 4.41, будет равна:

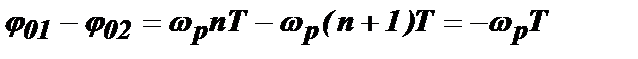
Тогда условие получения резонанса в контуре примет вид:

,

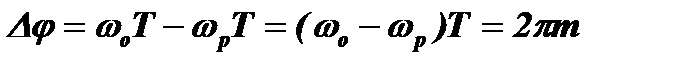где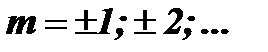

Если учесть, что 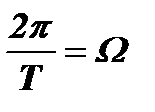- круговая частота повторения импульсов, то получим частоты ω_о, на которых будет происходить синфазное сложение откликов от отдельных импульсов и, следовательно, возникнут резонансы:

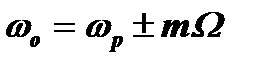
Таким образом, при подаче в контур последовательности радиоимпульсов. основной резонанс возникнет на частоте заполнения радиоимпульсов ω_р, а остальные резонансы будут располагаться относительно ω_р на частотах, кратных частоте повторения импульсов. При иных вариантах формирования радиоимпульсной последовательности могут быть получены другие значения начальных фаз j₀₁ и j₀₂. В этом случае резонансы в контуре будут располагаться на других частотах. Различные варианты накопительного резонанса в колебательном контуре при воздействии на него последовательности радиоимпульсов, будут рассмотрены в главе 5 "Спектры".

Различие в реакции контура на воздействие импульсного и непрерывного процессов. Это различие показано на рис. 4.45. При подаче на контур импульсного процесса и выполнении условий получения максимальной амплитуды свободных колебаний (τ=Т_δ/4) и возникновения резонанса (Δj=2πm) в нем происходит интенсивный рост амплитуды колебаний (рис. 4.45,а). Очевидно, что непрерывное колебание, из которого «вырезан» этот импульсный процесс, вносит в контур существенно большую мощность. Однако при его подаче на контур амплитуда колебаний в контуре не растет и резонанс, соответственно, не возникает (рис.4.45,б),

Это кажущееся противоречие можно объяснить следующим образом. Непрерывное колебание, поданное на контур, в течение одной четверти периода биений Т_δ/4 возбуждает колебания в контуре, а затем на протяжении следующей четверти периода Т_δ/4 полностью гасит эти колебания. Этот процесс повторяется периодически и в результате амплитуда колебаний в контуре не нарастает. Когда же непрерывный процесс превращается в импульсный, то внешнее колебание прекращается как раз в те промежутки времени, когда оно могло бы гасить колебания в контуре. В результате в контуре происходит только нарастание колебаний и создаются условия для резонанса.