Резонанс в контуре с переменными параметрами.

Системой с переменными параметрами (параметрической системой) называется система, у которой хотя бы один из параметров (сопротивление, индуктивность, емкость) изменяется во времени. В уравнении, описывающем такую систему, параметр является функцией времени.

Основное отличие параметрических систем от линейных и нелинейных систем с постоянными параметрами - возможность ввода и вывода энергии из системы через изменяемый реактивный параметр.

Для иллюстрации такой возможности рассмотрим классический пример. Заряды на пластинах заряженного конденсатора имеют разные знаки. Поэтому между пластинами возникают силы притяжения. Если увеличивать зазор между пластинами (уменьшать емкость конденсатора), то надо преодолеть действие этих сил и затратить на это механическую энергию, которая перейдет в энергию электрического поля конденсатора. Если зарядов на пластинах нет, то при изменении зазора передачи энергии не происходит. Если конденсатор подключен к источнику переменного напряжения, то можно раздвигать его пластины (уменьшать его емкость), когда напряжение достигнет максимума (положительного или отрицательного), и сближать их (увеличивать его емкость), при прохождении напряжения через нуль. В этом случае через конденсатор в систему будет непрерывно вводиться энергия из устройства, которое изменяет зазор конденсатора. Если, наоборот, раздвигать пластины, когда напряжение проходит через нуль и сближать их когда напряжение достигает максимума, то энергия будет непрерывно выводиться из системы через конденсатор к устройству, изменяющему зазор между пластинами. Рисунок 4. 23 иллюстрирует эту возможность.

Рис. 4.23

Введение энергии в систему через переменный параметр можно пояснить на таком механическом примере, как раскачивание качелей (рис. 4.24). Чтобы раскачаться, человек, стоящий на доске качелей, приседает в крайних (верхних) положениях качелей (а и в на рисунке) и резко распрямляется при проходе качелей через среднее (нижнее) положение (б и г на рисунке).

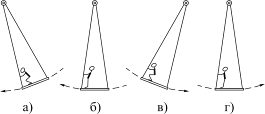
Рис. 4.24

Центр тяжести качелей при этом периодически поднимается и опускается, описывая траекторию, показанную на рисунке 4.25. Это действие эквивалентно изменению зазора в конденсаторе.

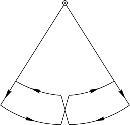
Рис. 4.25

Распрямляясь на движущихся качелях при их проходе через нижнее положение, человек развивает усилие, направленное навстречу радиальному (центростремительному) ускорению, которое зависит от скорости. Именно в этом положении человек распрямляется и изменяет положение центра тяжести, производя работу, аналогичную той, что происходит при увеличении зазора в конденсаторе, и добавляя энергию в систему. В верхних же положениях скорость и радиальное ускорение (напряжение на конденсаторе) равны нулю, и, приседая в этих положениях (сдвигая пластины), человек никакой работы не производит.

Чтобы раскачать качели указанным способом, необходимо, чтобы они находились в движении. Раскачать неподвижные качели нельзя, также как нельзя ввести энергию в конденсатор, изменяя его зазор, если на него не подано напряжение.

Таким образом, колебания поддерживаются вследствие периодического изменения параметра колебательной системы, которое называется параметрическим возбуждением системы. Параметрический способ возбуждения системы отличается от обычного, когда возбуждение осуществляется через положительную обратную связь. На механическом примере качелей видно, что возникающая в системе сила действует не в направлении совершающихся колебаний, а в направлении, перпендикулярном этому движению. Таким образом, эта сила непосредственно не "подталкивает" колебательную систему, а вводит в нее энергию, поддерживающую, увеличивающую или ослабляющую ее движение. Отметим также, что изменение длины маятника (реактивного параметра) в течение одного периода должно приводить к изменению частоты его колебаний.

Сформулируем основные особенности параметрических систем.

Первая особенность. Энергия может вводиться в систему как от основного источника (внешней ЭДС), так и через изменяемый реактивный параметр системы.

Вторая особенность. Количество энергии и направление обмена этой энергией между системой и источником изменения ее параметра зависит от соотношения фаз или временного сдвига между законом изменения этого параметра и законом изменения напряжения, включенного в систему внешнего источника.

Выше рассмотрены условия, при которых энергия или вводится или выводится из конденсатора. При других временных сдвигах между напряжением внешнего источника и моментами перемещением пластин конденсатора, обмен энергией в том или другом направлении будет происходить менее интенсивно или совсем не будет иметь места.

Третья особенность. Наибольшее количество энергии поступает в параметрическую систему через изменяемый параметр в том случае, когда частота изменения параметра вдвое превышает частоту напряжения внешнего источника. В случае изменения емкости конденсатора по гармоническому закону необходимо увеличивать расстояние между пластинами дважды за период колебаний внешнего источника, когда его напряжение проходит через положительный и отрицательный максимумы и уменьшать это расстояние в моменты прохождения этого напряжения через нуль.

В общем случае отношение частоты колебаний внешнего источника к частоте изменения параметра может равняться не только 1/2, но и 3/2, 5/2 и так далее. Тогда энергия будет вноситься в систему реже: через один, два, три и так далее "такта". Однако параметрические колебания возбуждаются и поддерживаются легче всего именно при отношении частот, равном 1/2.

Четвертая особенность. При изменении параметра форма собственных колебаний системы уже не повторяет форму гармонического напряжения внешнего источника, а принимает форму, зависящую от формы и параметров внешней силы, изменяющей параметр. Чтобы понять, как это происходит, перейдем к резонансу.

Напомним, что резонансом называется резкое увеличение амплитуды колебаний в системе под влиянием внешнего воздействия. В параметрической системе есть два источника такого воздействия: источник внешнего напряжения и источник, изменяющий параметр. Соответственно в параметрической системе может возникать два вида резонанса

1-й вид резонанса, подобный резонансу в колебательном контуре с постоянными параметрами, возникает, когда энергия поступает в контур от внешнего источника, а закон изменения внешнего напряжения близок к закону изменения собственных колебаний системы.

2-й вид резонанса называется "параметрическим возбуждением". Он связан с введением в контур энергии путем изменения параметра.

Оба эти резонанса могут существовать в контуре совместно.

Рассмотрим эти виды резонанса.

1-й вид резонанса возникает в параметрической системе под влиянием внешнего источника напряжения. Чтобы исключить влияние энергии, вводимой в систему с помощью параметрического воздействия, рассмотрим резонанс в колебательном контуре, когда переменным параметром является сопротивление (рис. 4.26). Для его изменения не надо производить работу и затрачивать энергию.

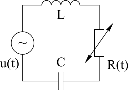
Рис. 4.26

Рассмотрим процессы, происходящие в этом колебательном контуре. Положим, что входное напряжение u(t) и переменное сопротивление r(t) изменяются по гармоническому закону с одинаковым периодом. На рисунке 4.27 приведены диаграммы изменения напряжения u(t), сопротивления r(t) и тока в цепи i(t) для трех значений фазового угла j между колебаниями напряжения и сопротивления:j=0⁰, j=90⁰, j=180⁰.

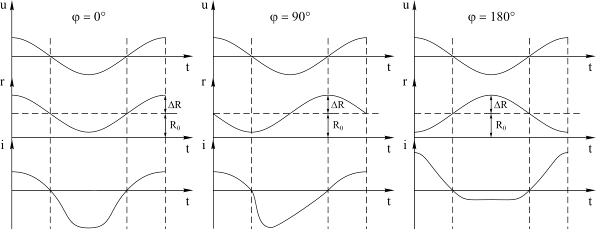
Рис. 4.27

Из рисунка 4.27 видно, что форма колебания в контуре с переменным сопротивлением: а) отличается от синусоиды и б) зависит от угла j. Это иллюстрирует четвертую особенность параметрической системы: отличие формы собственных колебаний параметрической системы от формы входных гармонических колебаний. Очевидно, что эта форма собственных колебаний зависит от закона изменения параметра.

Указанные свойства позволяют использовать цепь с переменным сопротивлением в качестве выпрямителя, амплитудного модулятора и детектора. Приведенный на рисунке 4.28 выпрямитель отличается от обычного выпрямителя с нелинейным элементом тем, что при сдвиге фазы между u(t) и r(t) на 90⁰, эффект выпрямления в параметрическом выпрямителе пропадает. Поэтому такой выпрямитель называется синхронным.

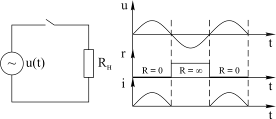
Рис. 4.28

Чтобы найти условия резонанса в контуре с переменным сопротивлением, необходимо, также как и в случае контура с постоянными параметрами, решить его дифференциальное уравнение, но теперь уже с переменным коэффициентом:

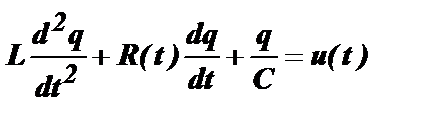
Решения этого уравнения в общем случае вызывает серьезные трудности. Для возникновения в этом контуре резонанса под воздействием внешнего источника необходимо, чтобы ток в контуре, имеющий, как мы видели несинусоидальную форму, вызывал на емкости и индуктивности контура падения напряжения, одинаковые по форме, но противоположные по знаку. В этом случае, так же как и в контуре с постоянными параметрами, произойдет взаимная компенсация реактивных сопротивлений емкости и индуктивности и наступит компенсационный резонанс.

Второй вид резонанса возникает при изменении реактивного параметра. Рассмотрим случай, когда переменным параметром является емкость C (рис. 4.29).

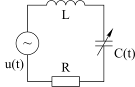
Рис. 4.29

Поскольку для роста амплитуды колебаний в контуре при резонансе необходимо, чтобы мощность, поступающая за период в контур от источника, изменяющего параметр, превышала потери мощности в контуре за этот же период, рассмотрим соотношение между мощностью, теряемой в контуре, и мощностью, поступающей в контур.

Средние потери мощности в контуре за период равны: .

Найдем мощность, поступающую в контур за период P₊. Энергия заряженного конденсатора равна: W=CU²/2. При уменьшении емкости на DС энергия увеличивается на . За период такое приращение происходит дважды: . Тогда мощность, вводимая в контур за период, равна: 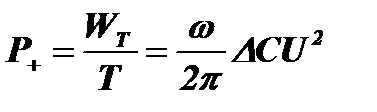. Учитывая, что I=U/X_c=UwC, запишем:

.

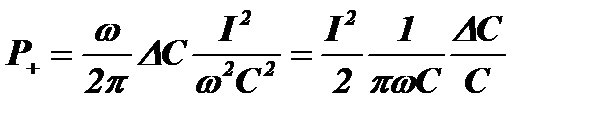Величина является отрицательным сопротивлением, вносимым в контур.

Если P₊>P_- или R₊<R_-, то возникает рост амплитуды колебаний в контуре или параметрический резонанс. Это явление также называют параметрическим возбуждением. Для ограничения роста амплитуды при параметрическом резонансе в схему вводится нелинейное сопротивление. В противном случае в схеме возникнет электрический пробой.

Если между напряжением внешнего источника и законом изменения параметра имеется сдвиг по фазе j (или временная задержка), то выражение для отрицательного сопротивления (при прямоугольном законе изменения параметра) примет вид: . При j=0⁰ cos 2j =1 и мощность в контур добавляется, при j=45⁰ cos 2j = 0 и мощность в контур не добавляется и не отнимается, а при j=90⁰ cos 2j= –1 и мощность у контура отнимается.

Теперь вернемся к решению дифференциального уравнения параметрического контура, которое позволит определить форму колебаний. Изменение заряда в таком контуре под действием ЭДС 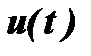описывается линейным дифференциальным уравнением с переменным коэффициентом:

,

где:

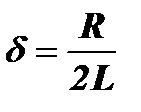; и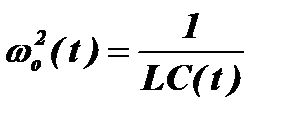

Решение этого уравнения найдено только для случая отсутствия внешней ЭДС и потерь, т.е. при u(t)=0 и R=0. В этом случае уравнение контура принимает вид: .

Это уравнение носит имя Хилла, впервые исследовавшего его в связи с задачами небесной механики. Наиболее детально это уравнение исследовано для частного случая, когда , т.е. для изменения частоты по гармоническому закону с частотой ω_п и относительной глубиной m:

Это уравнение носит имя Матье. Нетрудно видеть, что в случае, когда m=0, решением этого уравнения будут гармонические колебания с частотой ω_o. Следовательно, ω_o является частотой собственных колебаний невозмущенного контура.

Решение уравнения Матье имеет вид:

,

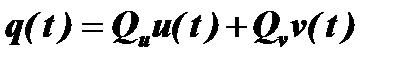где Q_u и Q_v - постоянные интегрирования;

u(t) и v(t) - функции Хилла, представляющие собой два линейно независимых квазипериодических частных решения.

Функции Хилла являются взаимно ортогональными и нормированными. При заданном периоде таких функций возможно бесчисленное многообразие их формы. В общем случае эта форма очень сложна (рис. 4.30), но по мере уменьшения параметра m функции Хилла все больше походят на гармонические и в предельном случае контура с постоянными параметрами для которого 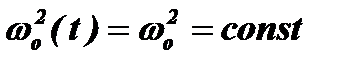, функция u(t) вырождается в косинусоиду, а v(t) - в синусоиду.

Рис. 4.30

Резонансными для параметрического контура могут быть лишь такие внешние ЭДС, которые с точностью до постоянного множителя воспроизводят форму собственных колебаний контура в отсутствие затухания.

Таким образом, в общем случае параметрический контур придает, "самостоятельное существование" и выделяет из состава произвольной внешней силы не гармонические составляющие, а некоторые функции Хилла, которые лишь для частного случая контура с постоянными параметрами вырождаются в синусоидальные, гармонические функции.

Особенности частотных характеристик параметрических систем первым исследовал Г. С. Горелик, который при изучении сверхрегенератора обнаружил необычное явление "кратного" резонанса. Сверхрегенератор представляет собой простой колебательный контур, настроенный на частоту принимаемой станции ω_o, у которого омическое сопротивление изменяется по гармоническому закону с частотой ω_п. Работая на метровых волнах Горелик обнаружил, что при достаточной добротности такой контур с переменным сопротивлением имеет резонансную кривую, показанную на рисунке 4.31 и принимает все станции, частота которых смещена относительно частоты настройки ω_o на величину кратную частоте изменения сопротивления ω_п (отсюда название "кратный" резонанс).

Рис. 4.31

Исследование этого явления стало началом развития теории параметрических систем.