Автокорреляция уровней динамического ряда и характеристика его структуры

При наличии тенденции в ряде динамики уровни ряда харак­теризуются автокорреляцией, т.е. каждый последующий уро­вень ряда зависит от предыдущего. Например, цена на то­вар сегодня, как правило, зависит от цены вчерашнего дня. Корреляционная связь между последовательными значения­ми уровней динамического ряда называется автокорреляци­ей уровней динамического ряда.

Для измерения автокорреляции уровней динамического ряда используется коэффициент автокорреляции уровней

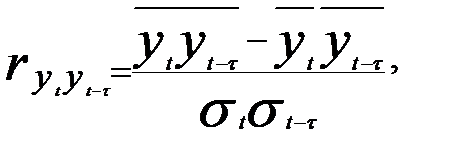(5.12)

где 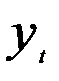— фактические уровни динамического ряда; 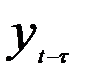— уровни того же динамического ряда, но сдвинутые на 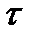шагов во времени; 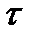— величина лага (сдвига во времени), принимающая значения 1, 2, 3,.... и определяющая порядок коэффициента автокорреляции.

При 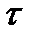= 1 рассчитывается коэффициент автокорреляции первого порядка, т.е. измеряется корреляция текущих зна­чений уровней динамического ряда 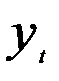, с предшествующими уровнями .

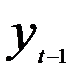При 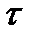= 2 изучается зависимость текущих уровней ряда y_tс уровнями этого же ряда, сдвинутыми на 2 временных шага 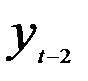, т.е. рассчитывается коэффициент автокорреляции второ­го порядка, а при 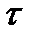= 3 — соответственно третьего поряд­ка, при 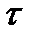- к — коэффициент автокорреляции к - го порядка.Чем длиннее динамический ряд, тем выше может быть поря­док коэффициента автокорреляции уровней.

Коэффициент автокорреляции уровней ряда практиче­ски рассчитывается по формуле линейного коэффициента корреляции. Поэтому его величина изменяется в пределах от -1 до +1. Чем ближе его величина к 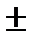1, тем сильнее зави­симость текущих уровней динамического ряда от предыдущих.

Если ряд характеризуется четко выраженной тенденцией, то для него коэффициент автокорреляции первого порядка приближается к +1. Так, для рассмотренного ранее ряда дина­мики заработной платы работника коэффициент автокорреля­ции уровней первого порядка составил 0,9987, демонстрируя тесную связь последующих уровней ряда от предыдущих.

Поскольку в примере рассчитывается коэффициент авто­корреляции первого порядка, т.е. когда 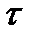= 1, формула его рас­чета приобретает вид

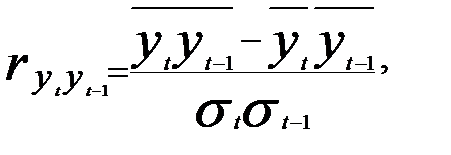(5.13)

где 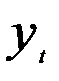— уровни ряда в момент времени t; 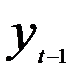— те же уровни ряда, но сдвинутые на год, т.е. уровни ряда в момент времени (t -1) (пре­дыдущий год).

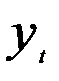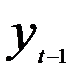Так как оба ряда ( и ) для расчета коэффициента авто­корреляции должны быть одинаковой длины, то первое зна­чение по ряду 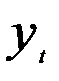в расчетах не участвует.

Например, для динамического ряда импорта России (в млрд. долл. США)

необходимые суммы для подсчета отдельных элементов фор­мулы коэффициента автокорреляции уровней составили

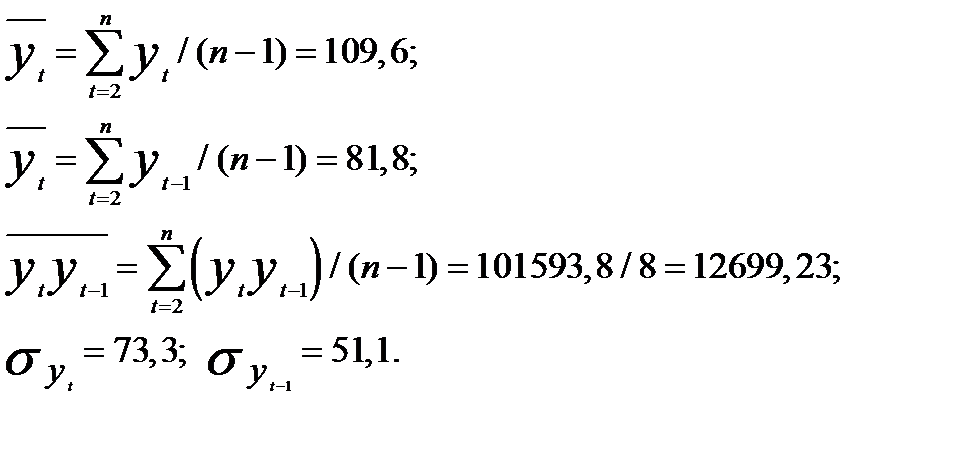
Соответственно коэффициент автокорреляции уровней со­ставит

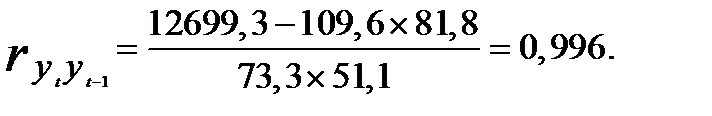
Методика расчета коэффициентов автокорреляции более высоких порядков та же, но при этом число коррелируемых пар уменьшается. В нашем примере их восемь (с t = 2 по t = 9). Если же увеличим лаг до 2 лет, т.е. 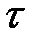= 2, то останется семь кор­релируемых пар (с t = 3 по t = 9), при 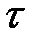= 3 будет шесть корре­лируемых пар (с t = 4 поt = 9). Ввиду уменьшения числа на­блюдений при расчете коэффициента автокорреляции уровней, увеличение величины лага не беспредельно: принято считать, что максимальная величина лага должна быть не более чем n/4 (п—длина динамического ряда). Для нашего примера при п = 9 максимальная величина лага составит 2 года ( 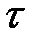= 2).

Коэффициент автокорреляции второго поряд­ка составит:

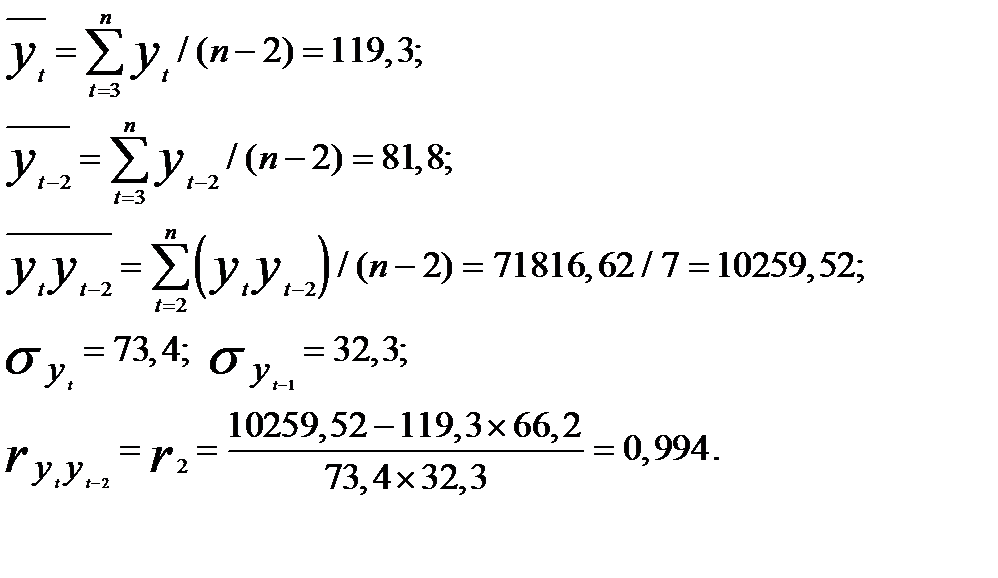
Коэффициенты автокорреляции разных порядков при­нято обозначать 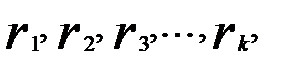где 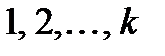указывает на но­мер порядка коэффициента автокорреляции.

В рассмотренном примере уровни динамического ряда име­ют тенденцию к возрастанию, и коэффициенты автокорреля­ции приближаются к +1. Аналогичная картина будет наблю­даться и при тенденции к уменьшению уровней динамического ряда.

Для стационарного динамического ряда с небольшими ко­лебаниями уровней, 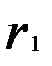достаточно близок к нулю и может принимать небольшое отрицательное значение. Так, предпо­ложим, что уровни ряда приняли следующие значения (пос­ледовательно во времени):

3; 1; 2; 1; 2; 1; 3; 3; 2; 3; 1; 2; 1; 1; 3; 3; 2; 2; 1; 3; 3; 2; 2; 3; 1; 2; 2; 1; 3; 1.

Серию коэффициентов автокорреляции уровней ряда с по­следовательным увеличением величины лага принято назы­вать автокорреляционной функцией (АКФ).

Для стационарного временного ряда с увеличением вели­чины лага взаимосвязь 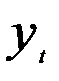и 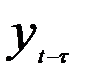ослабевает и АКФ характери­зуется монотонным убыванием, что графически должно пред­ставлять затухающую кривую.

По стационарному ряду АКФ оценивается исходя из форму­лы коэффициента автокорреляции

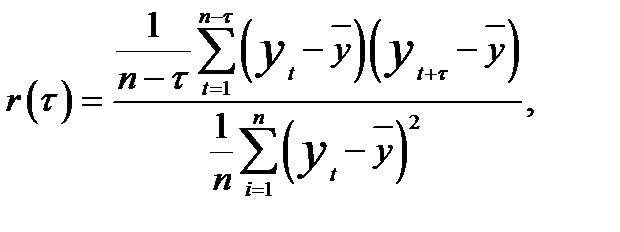(5.14)

где 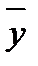— средняя арифметическая по исходному ряду.

В примере АКФ для стационарного ряда составила: 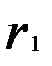= - 0,209; 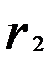= 0,056; 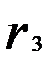= - 0,114; 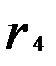= - 0,356; 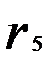= 0,057; 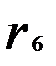= - 0,074; 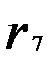= - 0,003. Однако при ограниченной длине ди­намического ряда рассмотренное поведение АКФ не всегда соблюдается.

АКФ дает представление о внутренней структуре динами­ческого ряда. С помощью АКФ можно определить наличие или отсутствие в ряду динамики периодических колебаний и соответственно величину периода колебаний: она равна той величине лага , при которой коэффициент автокорреляции уровней наибольший.

Для динамического ряда с монотонной тен­денцией к возрастанию (или уменьшению) уровней АКФ имеет значения, близкие k +1, которые медленно снижаются с воз­растанием величины лага.

Если ряд характеризуется сменой тенденций, то АКФ при­мет значения, стремительно уменьшающиеся с возрастанием величины лага, сопровождаемые иногда сменой знака коэф­фициента автокорреляции.

Знание АКФ может помочь при подборе модели рассматриваемого динамического ряда.