Специфика изучения взаимосвязей по рядам динамики
Временные ряды как источник информации накладывают отпечаток на методологию построения регрессионных моделей. Это связано с возможной ложной корреляцией и ложной регрессией. Высокая корреляция между уровнями временных рядов может иметь место и при отсутствии реальной связи между явлениями. Если, например прокоррелировать динамические ряды заработной платы и дорожно-транспортных происшествий, то можно обнаружить коэффициент детерминации, близкий к единице. Установление связи там, где ее на самом деле нет, означает, что имеет место ложная корреляция. Соответственно и уравнение связи в этом случае будет представлять собой ложную регрессию.
Наличие ложной корреляции и ложной регрессии связано с повышающейся тенденцией каждого из рядов динамики, с автокорреляцией их уровней. Поэтому при построении регрессионных моделей по рядам динамики требуется их предварительная специальная обработка.
Если ряды динамики характеризуются наличием тренда, то при построении модели регрессии надо учесть тренд, например исключить его. В противном случае корреляция уровней рядов динамики будет преувеличена (коэффициент корреляции будет близок к +1 при одинаковой тенденции в рядах и будет близок к -1 при противоположной тенденции). Предположим, что строится регрессия личных сбережений граждан от доходов населения по данным за ряд лет. Коэффициент детерминации при этом составил 0,95. Может показаться, что получен хороший результат и уравнение регрессии пригодно для прогноза. Однако анализируя остатки, мы обнаружим наличие в них автокорреляции. Следовательно, наше уравнение регрессии содержит систематическую погрешность, так как не учитывает влияние тенденции. Высокое значение коэффициента детерминации указывает лишь на то, что обоим рядам свойственна тенденция к повышению уровней. Наличие в двух рядах динамики детерминированного тренда приведет, естественно, к ложной регрессии, которой нельзя воспользоваться для прогнозирования, так как остатки будут автокоррелированы и оценка параметра регрессии окажется неэффективной и не являющейся оценкой теоретического параметра связи между переменными xt и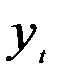 
. Модель регрессии по временным рядам пригодна для прогноза, только если остатки представляют собой стационарный ряд.
Если ряды динамики характеризуются не только тенденцией, но и периодическими колебаниями, то при построении модели регрессии следует учесть обе компоненты динамических рядов. В этом случае можно из первоначальных данных исключить как тенденцию, так и периодическую составляющую. Модель регрессии может быть построена либо по остаточным величинам, либо с включением в нее обоих компонент динамического ряда наряду с экономическими переменными.
Кроме того, изучая параллельные временные ряды, можно столкнуться с таким явлением, как временной лаг, т.е. запаздывание уровней одного ряда относительно другого. Например, спрос на товары длительного пользования может зависеть от доходов предыдущих лет. Инвестиции в основной капитал обычно зависят не только от прибыли текущего года, но и от прибыли прошлых периодов. Поэтому при изучении связи по рядам динамики сначала рассчитывается взаимная корреляционная функция, представляющая собой множество коэффициентов корреляции между уровнями рядов yt и xt, сдвинутыми относительно друг друга на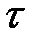 
моментов времени. Величина лага определяется по наибольшему коэффициенту корреляции. Если временной лаг существует, то он должен быть учтен в модели регрессии.
Определенные трудности при построении модели регрессии по временным рядам возникают в связи с проблемой мультиколлинеарности факторов, когда за счет тенденции объясняющие переменные оказываются тесно связанными между собой. Выходом из создавшегося положения может явиться построение модели регрессии по отклонениям от тренда.
Однако можно строить регрессию и по уровням рядов динамики, если удается при этом устранить автокорреляцию в остатках, применяя, например, обобщенный метод наименьших квадратов. Устранение автокорреляции в остатках возможно также путем изменения спецификации модели, включая, например, в правую часть модели регрессии лагированные (запаздывающие) переменные.
Дата добавления: 2016-03-22; просмотров: 1248;