Включение в модель регрессии фактора времени
Модель регрессии по двум временным рядам с включением в нее как отдельной независимой переменной фактора времени t имеет вид
y = a+bx+ct+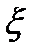 
, (5.19)
гдеt = 1, 2,3,..., п.
Включая в регрессию фактор времени t, устраняем линейную тенденцию из уровней временных рядов. Это объясняется спецификой множественной регрессии: коэффициенты регрессии показывают изолированное влияние на результат соответствующего фактора при неизменном уровне других факторов. В (5.19) коэффициент регрессии b характеризует «чистое» воздействие переменной х на результат у в условиях неизменной тенденции, т.е. при ее устранении.
Математически доказано, что если временные ряды характеризуются линейной тенденцией, то включение в модель фактора времени t равносильно построению модели регрессии по отклонениям от трендов с последующим переходом от нее к исходным уровням временного ряда зависимой переменной у.
В регрессии yt=a + bx + ct параметр b показывает, на сколько единиц изменяется в среднем у при изменении х на одну единицу в условиях неизменной тенденции; параметр с показывает средний абсолютный прирост у в условиях неизменного уровня объясняющей переменной х.
Принцип введения в модель фактора времени сохраняется и при изучении трех и более связанных рядов динамики. Так, если строится регрессия у =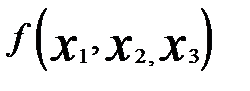 
, то включение в нее фактора времени t приводит чаще всего к модели вида
yt=a + b1x1+b2x2+b3x3+ct.
В ней параметры 
и 
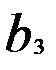показывают изолированное воздействие каждой объясняющей переменной на результат у, а параметр с — средний абсолютный прирост у в условиях неизменности значений переменных 
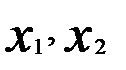и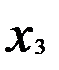 
.
Время в качестве независимой переменной часто вводится в виде линейного члена даже если другие переменные подвергаются логарифмированию или иному преобразованию.
Например, производственная функция с включением фактора времени часто записывается как
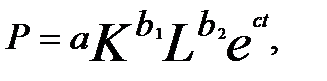
где Р —объем продукции; К —основной капитал; L —занятость; е — основание натурального логарифма; t — фактор времени, взятый как ряд натуральных чисел 1,2,..., п.
Если тенденция в рядах динамики характеризуется полиномом второй и более высоких степеней, то в модель регрессии вводятся t и t2, а иногда t в более высокой степени.
В этом случае рассматривается регрессия вида
у = a+bx+ct+dt2 (5.20)
при двух временных рядах
или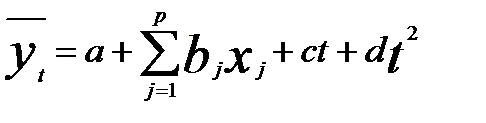 
(5.21)
при р временных рядах.
Вводя в модель регрессии фактор времени в виде t, t2,..., 
, предполагаем, что коэффициенты при переменных остаются во времени неизменными и характеризуют силу связи результата у с соответствующей объясняющей переменной х.
Если предполагается, что в регрессии коэффициенты при независимой переменной подвержены изменению во времени, то в модель можно ввести преобразованные переменные tx (где t — время). Оценка параметров модели дается МНК.
Модель регрессии с включением в нее фактора времени как независимой переменной не всегда эффективна ввиду возможной мультиколлинеарности факторов. Если временные ряды, используемые в регрессии, характеризуются четкой тенденцией (R2> 0,9), то корреляция t и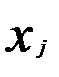 
может превышать корреляцию 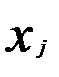с у, и параметры регрессии при объясняющих переменных х оказываются ненадежными и экономически не интерпретируемыми.
Время может быть учтено в регрессии и через использование лаговых переменных, т.е. запаздывающих переменных, сдвинутых на определенный интервал времени. Например, спрос на недвижимость в значительной мере определяется доходом не текущего, а предыдущих периодов.
Рассмотренные пути учета тенденции при построении модели регрессии по временным рядам не всегда дают желаемые результаты. Регрессия по отклонениям от тренда зачастую имеет низкий показатель детерминации. Регрессия с включением фактора времени нередко сводится лишь к модели тенденции ввиду статистической незначимости коэффициентов регрессии при объясняющих переменных. Но даже при статистической значимости модели регрессии и ее параметров может остаться автокоррелированность ошибок. Одним из методов ее устранения является обобщенный метод наименьших квадратов.
Дата добавления: 2016-03-22; просмотров: 2499;