Метод последовательных разностей

Если в ряде динамики имеется четко выраженная линей­ная тенденция, то ее можно устранить, перейдя от исход­ных уровней ряда y_t к цепным абсолютным приростам 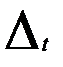, т.е. первым разностям. Объясняется это тем, что линейный тренд характеризуется постоянным абсолютным приростом. Его величина в уравнении 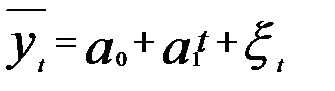соответствует пара­метру 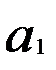. Первые разности в линейном тренде будут варьи­ровать за счет случайной составляющей 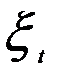вокруг своей константы — параметра 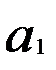. Тенденция в уровнях временно­го ряда будет устранена.

Если ряд динамики характеризуется тенденцией в виде па­раболы второй степени, то для ее устранения можно заменить исходные уровни ряда на вторые разности 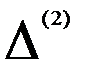, т.е. на величину абсолютных ускорений.

При исследовании двух динамических рядов с линейными тенденциями модель линейной регрессии примет вид

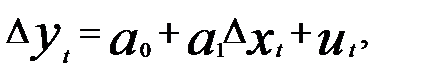(5.15)

где 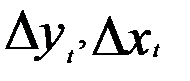— первые разности; 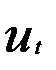— случайная ошибка.

Модель (5.15) по существу является моделью скорости роста. Она строится как обычная модель регрессии, но не по уровням динамических рядов, а по их приростам, т.е. по продифферен­цированным рядам.

Параметр 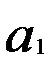в модели характеризует среднее изменение ско­рости ряда 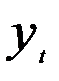с изменением абсолютного прироста ряда 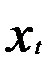на единицу.

Следует заметить, что если модель будет характеризовать­ся высоким показателем R² и отсутствием автокорреляции в остатках, то для прогнозирования конкретных значений y_tможно перейти к уравнению вида

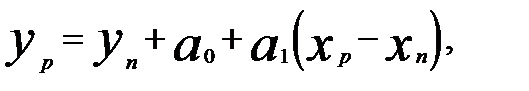(5.16)

где у_р — прогнозное значение динамического уровня ряда y_t; у_п — конечный уровень динамического ряда y_t; х_р — прогноз­ное значение уровня ряда 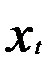, х_п — конечный уровень ряда .

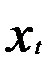В данном уравнении величина х_р-х_п = ∆х_р оценивает про­гнозное значение скорости ряда х, а у_р -у_п = ∆у_р — прогноз­ное значение скорости ряда у.

Прогнозное значение фактора х_р может быть дано либо по модели

x_t =f(z_t), где z_t — объясняющая переменная 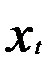_;, либо по тренду 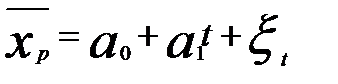. От того, насколько хорошо спрогнозировано значение фактора х_р, зависит качество прогноза у .