Метод отклонений от тренда
Как уже указывалось, метод отклонений от тренда является более точным методом исключения тенденции из данных временного ряда. Это связано не только с тем, что тенденция выражается в виде уравнения тренда любой математической функции. Рассматриваемые для модели регрессии ряды динамики могут иметь разные тенденции. Например, ряд xt описывается гиперболой, а ряд yt — параболой. В этом случае метод отклонений от тренда позволяет исключить из каждого временного ряда соответствующую ему тенденцию.
Алгоритм построения регрессии при применении метода отклонений следующий.
1. Для каждого временного ряда определяются уравнение тренда и теоретические значения yt; xt.
2. По каждому из рядов находятся остаточные величины
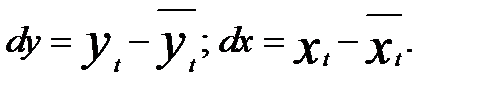
3. Строится модель регрессии
dy = f(dx). (5.17)
В линейной регрессии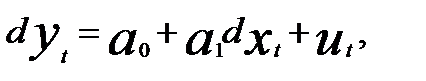 
параметр 
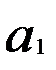показывает как в среднем изменяется величина случайных отклонений по ряду yt с изменением случайных колебаний ряда xtна единицу. Если при этом оба ряда характеризуются линейной тенденцией, то параметр 
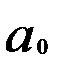= 0, так как 
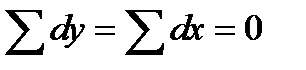. Тогда модель линейной регрессии примет вид 
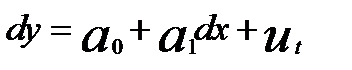и параметр 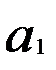будет выступать коэффициентом пропорциональности. Его величина будет показывать, во сколько раз случайные отклонения по ряду yt в среднем выше (ниже) случайных отклонений по ряду xt.
Для прогноза конкретных значений можно перейти к уравнению, связывающему между собой уровни временных рядов. С этой целью в модель регрессии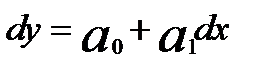 
подставим значения dy и dx, раскрыв их содержание, т.е.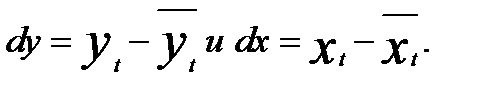 
Тогда имеем, например, для линейной регрессии 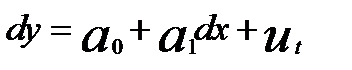, т.е. 
-
= 
+ 
( 
-
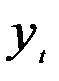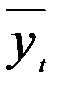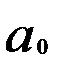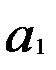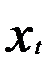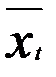),или 
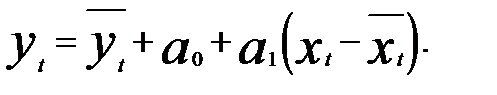
Данную модель можно использовать для прогноза
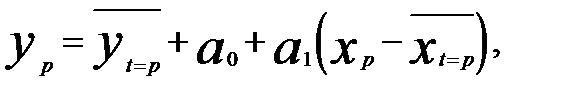(5.18)
где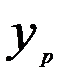 
—прогнозное значение у; 
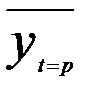—прогноз у по тренду при t = р; хр — прогнозное значение х, найденное либо по модели регрессии, либо как 
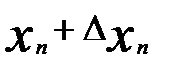; xt=p — прогноз х исходя из уравнения тренда при t = р.
Результат прогноза зависит от качества прогноза фактора х и от качества трендовых моделей, используемых в прогнозировании.
Дата добавления: 2016-03-22; просмотров: 1278;