Обобщенный метод наименьших квадратов при построении модели регрессии по временным рядам
Методы устранения автокорреляции в остатках могут быть разные. Они зависят от причин автокорреляции. Автокорреляция в остатках может быть следствием неправильной спецификации модели: не учтена важная объясняющая переменная, неправильно выбрана форма связи. В этом случае можно попытаться изменить математическую функцию регрессии (например, линейную на степенную), уточнить набор объясняющих переменных. Однако если эти попытки не увенчались успехом и автокорреляция в остатках имеет место, то для ее устранения можно применить обобщенный метод наименьших квадратов (ОМНК).
ОМНК можно использовать как для парной, так и для множественной регрессии. Для простоты и уяснения сути проблемы рассмотрим регрессию двух временных рядов
yt=a + bxt+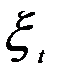 
. (5.22)
Для периода времени (t -1) справедливо равенство
yt-1=a + bxt-1+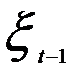 
. (5.23)
Если имеет место автокорреляция в остатках, т.е. последующие по времени остатки зависят от предыдущих, то регрессия остатков может быть представлена как
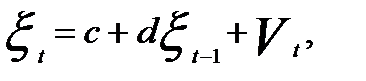(5.24)
где Vt — случайная ошибка для линейной регрессии остатков.
Но так как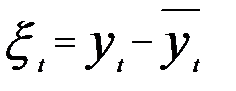 
то 
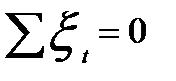и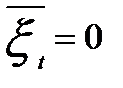 
. Полагая, что 
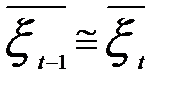имеем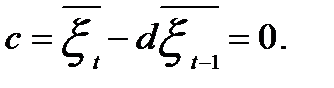 
Тогда регрессия остатков примет вид
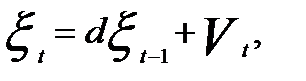(5.25)
Параметр d определим по формуле
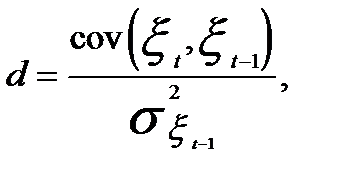(5.26)
где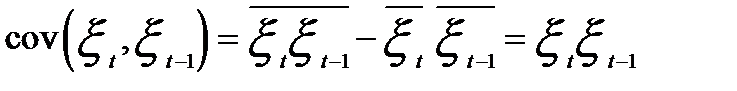 
В результате получим, что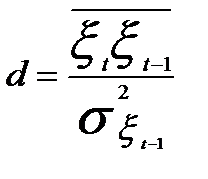 
. Предполагая, что 
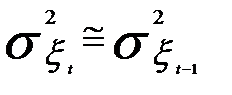, можно записать, что
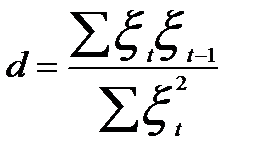, (5.26)
т.е. d — коэффициент автокорреляции остатков первого порядка. Обозначим его через ρ. Тогда регрессия остатков примет вид
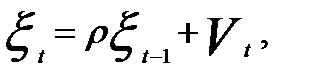(5.27)
где ρ — коэффициент автокорреляции остатков первого порядка; Vt — случайная ошибка, удовлетворяющая всем предпосылкам МНК.
Предполагая, что ρ известен, вычтем из уравнения (5.23) уравнение (5.22), умноженное на ρ:
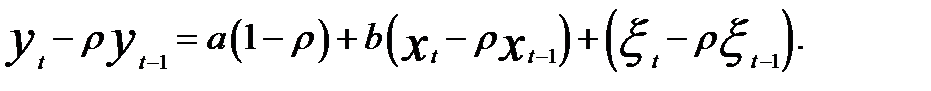(5.28)
Введём обозначения:
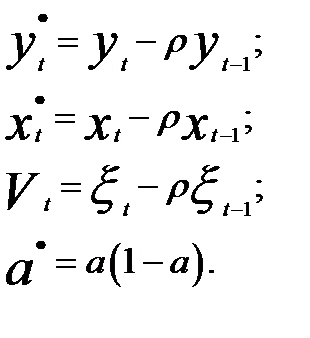
Тогда получим следующее уравнение
у* =а +bx*+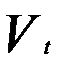 
, (5.29)
где Vt — независимые случайные величины, имеющие нормальное распределение.
Так как ошибки Vt удовлетворяют предпосылкам МНК (они не содержат автокорреляцию), то оценк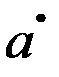и 
и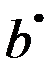 
будут обладать свойствами несмещенных оценок и могут быть получены обычным МНК.
Уравнение (9) возможно только при t> 1, так как при t = 1 отсутствует лаговая переменная. Чтобы не уменьшать число степеней свободы рекомендуется для первого периода времени (t = 1) использовать поправку Прайса — Уинстена
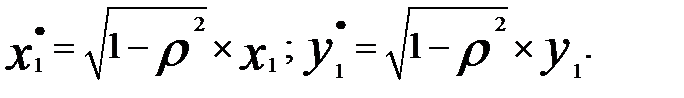(5.30)
Таким образом, ОМНК предполагает, что вместо исходных переменных yt и xtиспользуются взвешенные переменные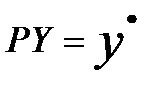 
и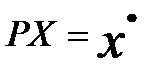 
,
где P – веса. В матричном виде модель регрессии принимает вид PY = PXB + P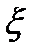 
.
В ней матрица весов Р составит
Иными словами, матрица исходных данных трансформируется
Для длинных динамических рядов поправка Прайса — Уинстена может не применяться. Тогда матрица весов не содержит первую строку рассмотренной матрицы Р, и в расчетах используется (n-1) преобразованных наблюдени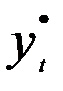й 
и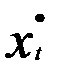 
.
К преобразованным переменным 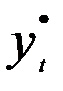и 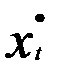применяется традиционный МНК и оцениваются параметры 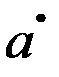и 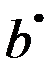. Далее из соотношения 
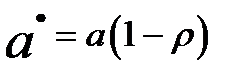можно найти параметр 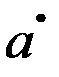как
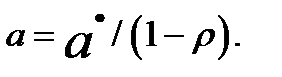(11)
ОМНК распространяется и на случай множественной регрессии
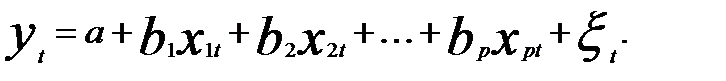
Если имеет место автокорреляция остатков и 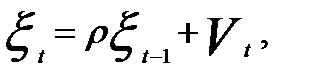то
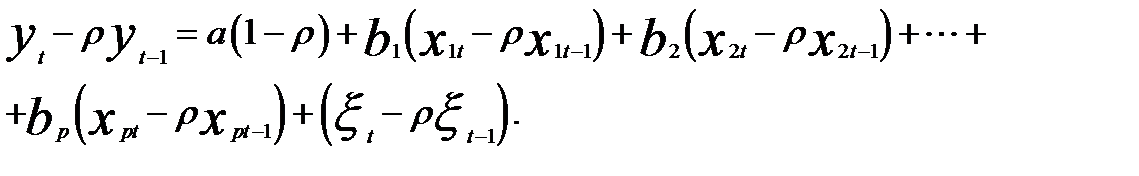
Или, исходя из прежней символики, строим модель вида
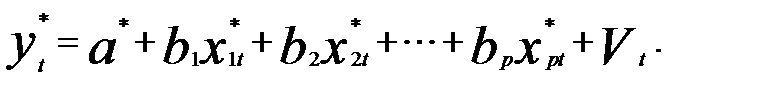(5.31)
Применяя к переменным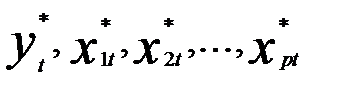 
традиционный МНК, найдем оценки параметров 
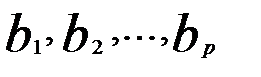. Свободный член модели определим как 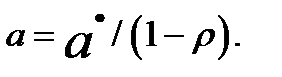Далее можно написать искомую модель регрессии yt =a + blxlt + ...+bpxpt, в которой устранена автокорреляция остатков.
Иными словами, применение ОМНК к регрессии с автокоррелированными остатками сводится к двухшаговой процедуре:
— преобразование исходных уровней динамических рядов с помощью известного значения коэффициента автокорреляции остатков первого порядка р;
— применение к преобразованным данным обычного МНК.
Дата добавления: 2016-03-22; просмотров: 2107;