Модели с распределенными лагами

Интерпретация параметров модели с распределенными лагами

Модели с распределенными лагами бывают двух типов:

— с конечным числом лагов

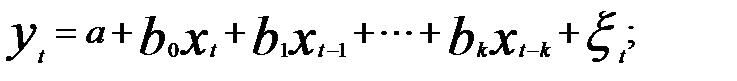(5.38)

— с бесконечным числом лагов

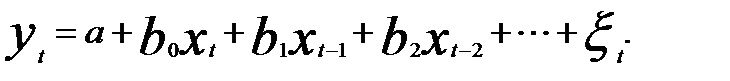(5.39)

Практическое применение чаще имеют модели с конечным числом лагов, т.е. модели, в которых число лагов экспериментально определено.

Предположим, рассматривается модель, в которой k = 4, т.е. 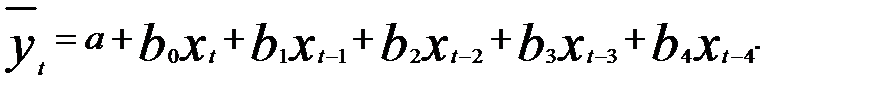Данная модель означает, что изменение во времени t объясняющей переменной х будет влиять на значения результативного признака в течение 4-х следующих моментов времени.

Коэффициент b0 называют краткосрочным мультипликатором, так как он характеризует среднее изменение результата упри изменении на 1 ед. своего измерения в фиксированный момент времени t.

В момент времени ( 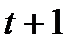) воздействие объясняющей переменной х на результат у составит ( 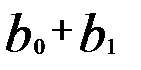) единиц, а в момент времени (t + 2) общее изменение составит 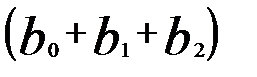единиц.

Любую сумму коэффициентов 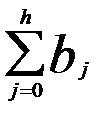, где h<k называют промежуточным мультипликатором, а сумму всех коэффициентов регрессии 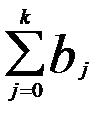— долгосрочным мультиплипликатором, который характеризует общее изменение у через k интервалов времени под воздействием изменения х в момент t на 1 ед.

При k = 4 долгосрочный мультипликатор составит ( 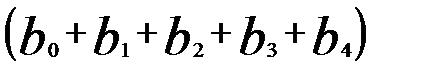. Он характеризует общее среднее изменение у через четыре временных интервала при увеличении х в момент времени t на 1 ед., а промежуточные мультипликаторы

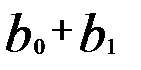( ) — изменение в момент времени (t + 1);

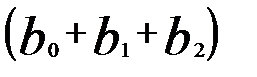— изменение в момент времени (t + 2);

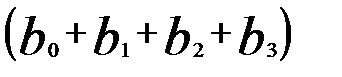— изменение в момент времени (t + 3).

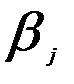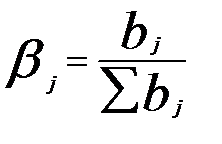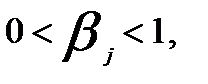Если все коэффициенты регрессии имеют одинаковые знаки, т.е. характеризуются однонаправленным изменением y в исследуемые kмоментов времени, то можно определить относительные коэффициенты модели , т.е. , где a 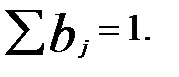Иными словами, 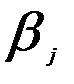характеризует долю общего изменения y в момент времени (t + j).

Предположим, что регрессия основных производственных фондов (у — в млн. руб.) в зависимости от размера инвестиций (х — в млн. руб.) характеризуется уравнением 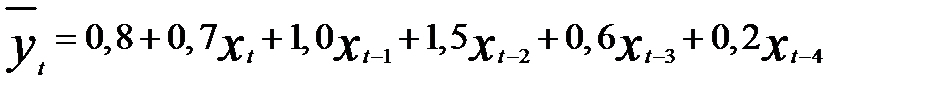, где t — года.

Анализ уравнения показывает, что рост инвестиций на 1 млн руб. в текущем периоде приводит к росту основных производственных фондов:

— в том же периоде — на 0,7 млн. руб. (краткосрочный мультипликатор);

— через 1 год — на 0,7 + 1 = 1,7 млн. руб.;

— через 2 года — на 0,7 + 1 + 1,5 = 3,2 млн. руб.;

— через 3 года — на 3,8 млн. руб. (промежуточный, как и предыдущие два, мультипликатор);

— через 4 года — на 4 млн. руб. (долгосрочный мультипликатор).

Относительные коэффициенты модели составят

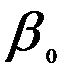= 0,7/4 = 0,175;

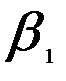= 1/4 = 0,25;

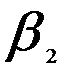= 1,5/4 = 0,375;

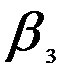= 0,6/4 = 0,15;

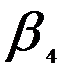= 0,2/4 = 0,05.

Следовательно, в текущем году реализуется 17,5% воздействия увеличения инвестиций на рост основных производственных фондов, а через год — еще 25%. Через 2 года — еще 37,5%, через 3 года — еще 15% и через 4 года — еще 5%.

Относительные коэффициенты модели 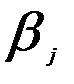можно использовать как весовые коэффициенты для расчета средней величины лага по средней арифметической:

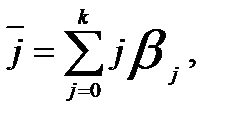
где j — величина лага.

Величина 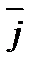показывает средний интервал времени, в течение которого будет происходить изменение зависимой переменной упод воздействием изменения объясняющей переменной х в момент времени t. Чем меньше величина среднего лага, тем быстрее реагирует результат у на изменение х. И наоборот, высокое значение среднего лага показывает, что воздействие объясняющей переменной на результат будет сказываться с течением длительного промежутка времени. В рассматриваемом примере величина среднего лага составит

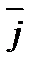= 0 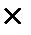0,175 + 1 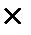0,25 + 2 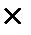0,375 + 3 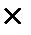0,15 + 4 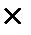0,05 = 1,65 года.

Следовательно, основная часть эффекта увеличения инвестиций проявляется через 1,65 года. Кроме среднего лага можно рассчитывать медианный лаг 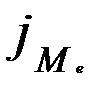, т.е. тот период времени, в течение которого с момента времени t будет реализована половина общего эффекта воздействия объясняющей переменной х на результат у. Для медианного лага справедливо равенство

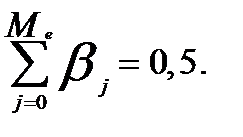
В нашем примере медианный лаг составляет 2 года, т.е. увеличение инвестиций в период времени t на 1 млн. руб. приводит к росту размера основных производственных фондов через 2 года на величину, составляющую половину долгосрочного мультипликатора, т.е. на 2 млн руб. Наибольший аналитический интерес представляет расчет величины медианного лага для моделей с большим числом лаговых переменных.