Интерпретация параметров модели авторегрессии

Для модели (5.51), как и в модели с распределенными лагами, параметр 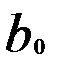характеризует краткосрочное изменение у, под воздействием изменения 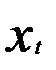на одну единицу. Параметр 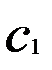по существу представляет собой величину λ из преобразования Койка, т.е. 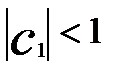, и показывает коэффициент снижения лаговых коэффициентов при увеличении величины лага в соответствии с концепцией их геометрического убывания. Следовательно, к моменту времени (t + 1) результат у изменится дополнительно на 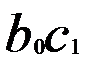, а к моменту времени (t +2) дополнительное изменение у составит 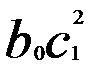единиц, к моменту времени (t +3) — 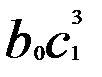единиц и т.д. Соответственно долгосрочный мультипликатор окажется равным

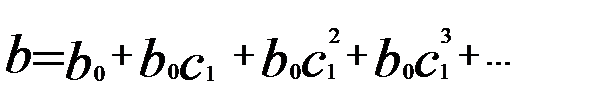
(в предположении бесконечного числа лагов).

С учетом геометрической прогрессии лаговых коэффициентов величина долгосрочного мультипликатора составит

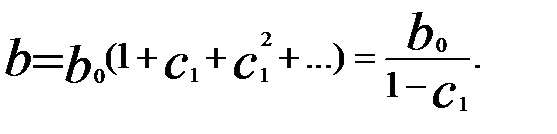
Предположим, что по региону по данным временных рядов построена модель авторегрессии, описывающая зависимость сбережений на душу населения за год ( 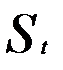— в тыс. ден. ед.) от среднедушевого совокупного годового дохода ( 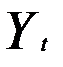— в тыс. ден. ед.) и сбережений предшествующего года ( ))

.

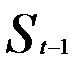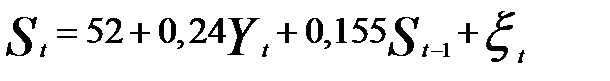Уравнение показывает, что краткосрочное изменение размера сбережений с ростом дохода на 1 тыс. ден. ед. составляет в том же году 0,24 тыс. ден. ед.Через год рост дохода на 1 тыс. ден. ед. увеличит размер сбережений на 0,276 тыс. ден. ед. (0,24 + 0,24 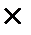0,15), т.е. дополнительно за год прирост составит 0,036 тыс. ден. ед. В дальнейшем величина дополнительного прироста будет убывать. Долгосрочный мультипликатор окажется равным 0,282 тыс. ден. ед. (0,24/0,85). Его величина характеризует прирост сбережений в долгосрочной перспективе с ростом дохода на 1 тыс. ден. ед.