Авторегрессионные процессы
Рассмотренные ранее модели авторегрессии содержали в правой части наряду с лаговыми зависимыми переменными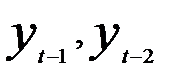 
и т.д. независимые переменные х. Авторегрессионная модель, в которой отсутствуют независимые переменные и yt рассматривается как линейная функция только предыдущих своих значений, представляет собой авторегрессионный процесс
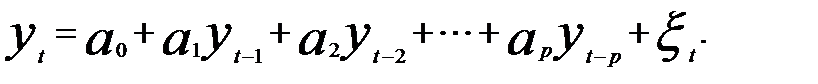(5.59)
В зависимости от того, сколько предыдущих уровней временного ряда включено в уравнение (5.59), авторегрессионный процесс может быть разного порядка. Если текущее значение уровня динамического ряда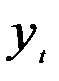 
рассматривается как линейная функция от одного предыдущего значения, то имеем дело с авторегрессионным процессом первого порядка (AR(1), что обычно в англоязычной литературе обозначается как AR(1).
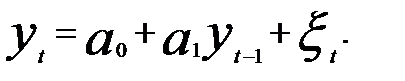(5.60)
Процессы AR могут быть стационарными и нестационарными. Чтобы процесс был стационарным, коэффициенты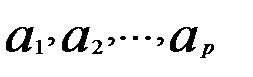 
в модели (5.59) должны образовывать сходящийся ряд и все корни характеристического уравнения 
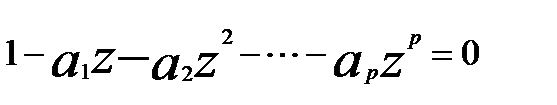(вещественные и комплексные) должны лежать вне единичного круга, т.е. 
.
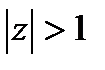Рассмотренное условие стационарности для процесса AR(1) означает, что в уравнении (5.60) параметр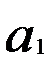 
должен соответствовать величине |а| < 1, так как характеристическое уравнение 1- 
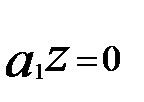имеет корень 
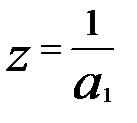и |z|>l при | 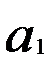|<1.
Авторегрессионный процесс с большим числом лагов предполагает очень длинные динамические ряды, которые далеко не всегда имеются в эконометрических исследованиях.
При наличии коротких временных рядов стационарные AR - процессы могут иметь место после удаления из уровней ряда тенденции и сезонных колебаний. Это означает, что исследователь должен вычленить эти компоненты динамического ряда и подвергать дальнейшей обработке остаточные величины. В этом случае авторегрессионный процесс первого порядка AR(1) примет вид
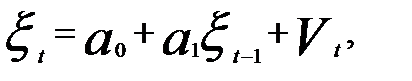(5.61)
где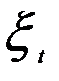 
— остатки после устранения из уровней ряда 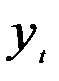тенденции и периодической составляющей; Vt — белый шум.
Дата добавления: 2016-03-22; просмотров: 1888;