Оценка автокорреляции остатков по модели авторегрессии

Рассмотренный ранее критерий Дарбина — Уотсона не применим для моделей авторегрессии, содержащих в составе объясняющих переменных лаговые значения зависимой переменной. Связано это с тем, что критерий Дарбина — Уотсона для модели авторегрессии может принимать значение, близкое к двум, как при отсутствии, так и при наличии автокорреляции остатков.

Предположим, что в модели авторегрессии (5.51) имеет место автокорреляция остатков, т.е. случайное отклонение можно рассматривать как авторегрессию вида

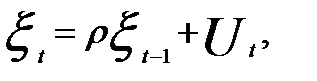(5.56)

где ρ — коэффициент автокорреляции первого порядка; Ut — случайная составляющая.

Тогда уравнение (5.51) можно представить как

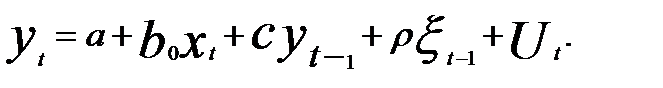(5.57)

В уравнении (5.57) 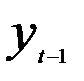связан с 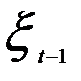как и по уравнению (5.51) 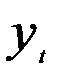связан с 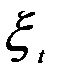. Таким образом, имеется систематическая связь лаговой зависимой переменной со случайной компонентой. Применение теста Дарбина — Уотсона к модели (5.57) может показать отсутствие автокорреляции в остатках Ut при наличии ее для остатков 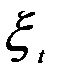. В связи с этим Дж. Дарбин предложил для моделей авторегрессии при оценке существенности автокорреляции остатков использовать другой критерий, который в литературе получил название

h-статистика Дарбина:

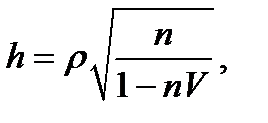(5.58)

где ρ — коэффициент автокорреляции в остатках первого порядка, который практически используется при расчете критерия Дарбина — Уотсона, т.е.

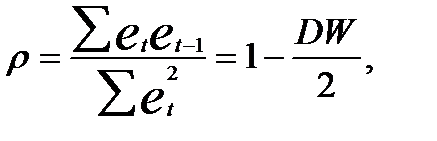
n— число наблюдений в модели; V — выборочная дисперсия коэффициента при лаговой зависимой переменной .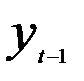

При большом числе наблюдений и при отсутствии в остатках автокорреляции первого порядка h-статистика Дарбина подчиняется стандартизированному нормальному распределению, Поэтому фактическое значение h сравнивается с табличным по заданному уровню значимости α. Если |h| больше критического значения, то нулевая гипотеза об отсутствии автокорреляции ошибок отклоняется. При практических расчетах чаще всего α берется как 0,05 и если |h| > 1,96, то гипотеза об отсутствии автокорреляции остатков отвергается.

Из уравнения (15) следует, что h-статистика не применима, если величина (nV) > 1. Кроме того, данный критерий предназначен для больших выборок (например, для n> 30). h-статистика зависит от квадрата стандартной ошибки параметра только при лаговой зависимой переменной 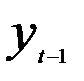(V) и не зависит от числа лагов, используемых в модели авторегрессии.

В рассматриваемом примере автокорреляция остатков не устранена, о чем свидетельствует h-статистики Дарбина: коэффициент автокорреляции в остатках ρ составил 0,440; стандартная ошибка коэффициента регрессии при переменной 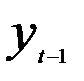оказалась равной 0,1635 (0,7946/4,86); соответственно V = 0,02673 и при n=23 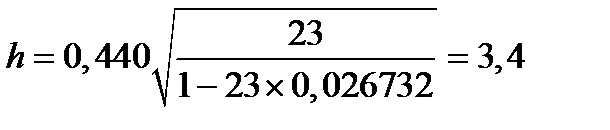, что больше необходимого 1,96.

Автокорреляция в остатках по авторегрессионным моделям может быть устранена с помощью авторегрессионных преобразований с использованием моделей ARMA иARIMA.

Авторегрессионные процессы и их моделирование (общая характеристика)