Методология построения модели ARIMA для исследуемого временного ряда включает следующую последовательность шагов.
На первом шаге необходимо получить стационарный ряд. При тестировании исходных данных на стационарность прежде всего используется визуальный анализ графика. Например, уже на этом этапе можно обнаружить ярко выраженную трендовую составляющую.
Также в методике Бокса—Дженкинса рекомендуется проводить анализ АКФ (ЧАКФ). Быстрое убывание значений выборочной АКФ является простым критерием стационарности (аналогичное поведение должна демонстрировать и ЧАКФ).
Часто на этом этапе используются статистические тесты на наличие единичного корня (тест Дики—Фуллера, расширенный тест Дики- Фуллера).
Для перехода к стационарному ряду традиционно применяют оператор взятия последовательных разностей (процедуру дискретного дифференцирования). Быстрое затухание АКФ будет свидетельствовать о том, что необходимая для стационарности ряда степень разности достигнута.
На втором шаге после получения стационарного ряда исследуется характер поведения выборочных АКФ и ЧАКФ, выдвигаются гипотезы о значениях параметров p (порядок авторегрессии) и q (порядок скользящего среднего).
При этом следует иметь в виду, что выборочные корреляционные функции могут не демонстрировать детального сходства с теоретическими. Поэтому для идентификации модели могут использоваться главные черты АКФ, при расхождении более тонких деталей, в результате формируется базовый набор, включающий 1—2 или даже большее число моделей.
На третьем шаге после осуществления идентификации моделей необходимо оценить их параметры. В современных эконометрических пакетах прикладных программ используются разные подходы (МНК, нелинейный МНК, метод максимального правдоподобия (ММП)). Все эти оценки при больших объемах выборок асимптотически эквивалентны.
На следующем, четвертом шаге для проверки каждой пробной модели на адекватность анализируется ряд ее остатков. У адекватной модели остатки должны быть похожими на белый шум, т. е. их выборочные автокорреляции не должны существенно отличаться от нуля.
При проверке значимости коэффициентов АКФ используются два подхода:
■ проверка значимости каждого коэффициента автокорреляции отдельно;
■ проверка значимости множества коэффициентов автокорреляции как группы.
Первый подход опирается на работу Бартлетта, показавшего, что если модель адекватна исходным данным и ошибки представляют собой белый шум, то распределение коэффициентов автокорреляции приближается к нормальному с нулевым математическим ожиданием и дисперсией 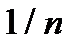 , т.е. к
, т.е. к 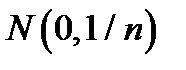 .
.
Поэтому если выборочный коэффициент автокорреляции 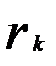 выходитза интервал
выходитза интервал 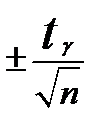 , то нулевая гипотеза о равенстве нулю коэффициентарк отвергается.
, то нулевая гипотеза о равенстве нулю коэффициентарк отвергается.
Второй подход опирается на Q-статистику Бокса—Пирса, позволяющую проверить равенство нулю сразу т первых значений АКФ остатков. Q-статистика определяется как
Q = n 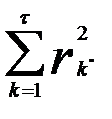
При нулевой гипотезе об отсутствии автокорреляции статистика Qимеет 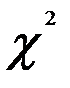 -распределение с v = τ-p-q степенями свободы, где р,q-параметры ARMA модели.
-распределение с v = τ-p-q степенями свободы, где р,q-параметры ARMA модели.
Если Q> 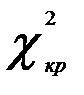 , то как группа первые τ коэффициентов автокорреляции значимы (т. е. не все
, то как группа первые τ коэффициентов автокорреляции значимы (т. е. не все 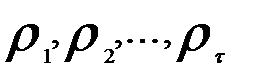 , равны нулю).
, равны нулю).
В некоторых эконометрических пакетах включена модификация этого подхода — тест Бокса-Льюнга. Соответствующая статистика в этом случае определяется выражением:
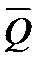 = n(n+ 2)
= n(n+ 2) 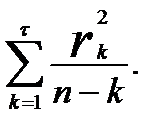
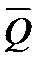 имеет такое же асимптотическое распределение, как и Q, однако ее распределение ближе к
имеет такое же асимптотическое распределение, как и Q, однако ее распределение ближе к 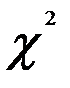 для конечных выборок. В практических руководствах рекомендуется рассматривать
для конечных выборок. В практических руководствах рекомендуется рассматривать 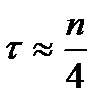 (но не более 50).
(но не более 50).
Кроме того, при построении модели ARIMA необходимо проверить значимость коэффициентов (по t-критерию). При этом модель не должна содержать лишних параметров, т. е. уменьшение числа параметров будет способствовать появлению значимой автокорреляции остатков.
Если в результате проверки несколько моделей оказываются адекватными исходным данным, то при окончательном выборе следует учесть два требования:
■ повышение точности (качество подгонки модели);
■ уменьшение числа параметров модели.
Воедино эти требования сведены в информационном критерии Акайка (Akaikeinformationcriterion (AIC)), определяемом формулой:
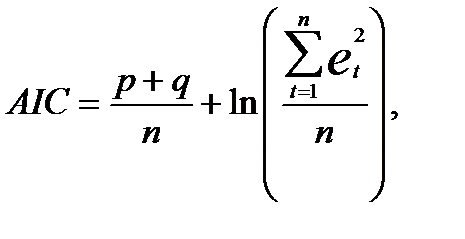
где 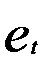 — уровни ряда остатков.
— уровни ряда остатков.
Очевидно, что выбор следует сделать в пользу модели с меньшим значением AIC.
Аналогичный характер носит критерий Шварца (Schwarzcriterion), усиливающий требование уменьшения количества параметров модели:
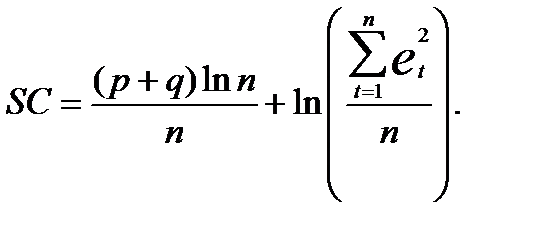
На заключительном этапе с помощью модели, выбранной на четвертом шаге, можно строить точечный и интервальный прогноз на L шагов вперед.
Сезонная модель Бокса—Дженкинса может быть представлена в виде: ARIMA(p, d, q)(Ps, Ds, Qs),где к параметрам модели р, d, q добавлены: Ps — сезонный параметр авторегрессии; Qs — сезонный параметр скользящего среднего; Ds— параметр, определяющий порядок сезонной разности (сезонной производной).
При наличии ярко выраженной сезонной компоненты целесообразно включение в модель сезонного дифференцирования. Однако при решении практических экономических задач не рекомендуется использовать сезонные производные больше первого порядка. Также лучше не применять модели, у которых сумма порядков разностей (сезонных и несезонных) больше двух, т. е. желательно выдерживать соотношение:
d+Ds ≤ 2.
Определение значений параметров сезонной авторегрессии SAR(Ps) и сезонного скользящего среднего SMA(Ds) также опирается на исследование АКФ и ЧАКФ. Только теперь все типичные проявления, всплески будут удалены друг от друга на величину лага S, где S — период сезонности.
При идентификации полной сезонной модели ARIMA(p, d, q)(Ps,As, Qs) часто сначала используют процедуру логарифмирования исходного ряда (для снижения дисперсии процесса), затем берут одну несезонную и одну сезонную разности (дифференцирование для несезонной части может и не потребоваться). На следующем этапе исследуется поведение АКФ и ЧАКФ для полученного производного ряда.
В некоторых эконометрических пакетах реализованы процедуры автоматического подбора структуры модели Бокса—Дженкинса.
Однако окончательный выбор модели все же должен оставаться за исследователем-экспертом, хорошо представляющим предметную область. Иногда можно построить две модели, одинаково хорошо соответствующие данным на ретроспективном участке (например, модель с порядком дифференцирования 1 и АR-членами и модель с большим порядком дифференцирования и MA-членами). Однако предлагаемые прогнозы у этих моделей могут существенно различаться. Поэтому окончательный выбор между такими моделями должен опираться на представления исследователя о виде нестационарности исходного ряда, о характере его трендовой составляющей.
Успех применения мощного, гибкого, но в то же время сложного аппарата модели ARIMA во многом зависит от практического опыта и квалификации исследователя, а процедуры автоматического выбора вида модели призваны лишь облегчить его аналитическую деятельность.
Пример 5.8.Известны данные экспорта и импорта РФ (в млрд. долларов США) за период с 1-го квартала 2002 года по второй квартал 2015 года. Требуется осуществить прогноз с применением модели ARIMAна 3-й и 4- кварталы 2015 года.
Рассмотрим более подробно динамические ряды экспорта и импорта. Их данные представлены в табл.5.13, а графическая иллюстрация -на рисунке 5.11.
Экспорт и импорт РФ
Таблица 5.13
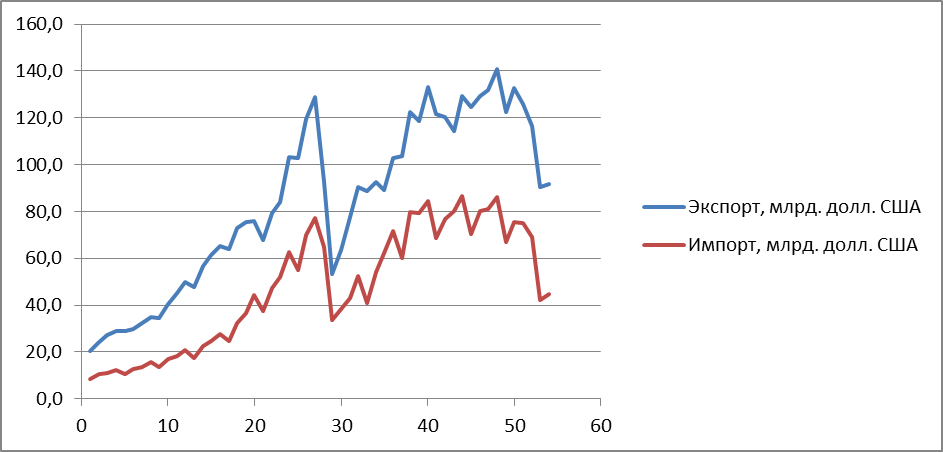
Рис. 5.11. Динамические ряды экспорта и импорта РФ
В период с 3-го квартала 2008 по 1- квартал 2009 гг. наблюдается влияние мирового финансового кризиса – объемы экспорта за этот период снизились на 77,5 млрд. долл., а импорта – на 43,8 млрд. долларов.Восстановительный период завершился по экспорту в 4-ом квартале, а по импорту – во 2-ом квартале 2011 года.
Следующее снижение объёмов экспорта и импорта наблюдается со 2-го квартала 2014 года. В первом квартале 2015 года по экспорту оно составило 42,6, а по импорту – 33,4 млрд. долларов США. По сравнению с соответствующим кварталом 2013 года объёмы экспорта снизились на 32,0%, а импорта – на 44,2%.
Из полученного графического изображения можно выдвинуть предположение о наличии систематической и сезонной компонент, а так же случайной компоненты. Наличие систематической компоненты можно объяснить присутствием долговременно действующих факторов, формирующих динамику (график имеет постоянную тенденцию к возрастанию). Наличие же сезонной компоненты объясняется присутствием колебаний на графике (выбросов) с определенной периодичностью. Объемы экспорта и импорта увеличиваются к декабрю каждого года и резко снижаются в январе следующего за ним.
В целях уменьшения вариации результативных признаков, обусловленной различным количеством рабочих часов в кварталах года, введем в качестве результативных переменных объёмы экспорта и импорта в час.
Кроме того, в процессе решения берётся натуральный логарифм, преследуя ранее упомянутую цель.
Рис. 5.12. Логарифм экспорта (в час) РФ
Для прогнозирования будем использовать модель ARIMA с интервенцией. Особенностью данной модели является возможность учёта спада в динамике внешнеторгового оборота под влиянием мирового финансового кризиса.
Наличие основной тенденции означает, что ряд данных не является стационарным. На этапе идентификации модели ARIMA необходимо добиться того, чтобы ряд первоначально нестационарный стал стационарным; это означает, что его среднее постоянно, а выборочные дисперсия и автокорреляция не меняются во времени. По этой причине обычно необходимо брать последовательные разности ряда до тех пор, пока ряд не станет стационарным. Для того чтобы определить необходимый порядок разности, нужно исследовать график ряда и автокоррелограммы.
Сильные изменения уровня (сильные скачки вверх или вниз) обычно требуют взятия несезонной разности первого порядка. Сильные изменения наклона требуют взятия разности второго порядка. Сезонная составляющая требует взятия соответствующей сезонной разности. Если имеется медленное убывание выборочных коэффициентов автокорреляции в зависимости от лага, обычно берут разность первого порядка.
В результате проведенного анализа было выявлено, что наиболее подходящим является взятие первых и четвертых разностей для устранения тренда и сезонности ряда.
В итоге формируется график разностей (рис.5.13). Из графика на рис. видно, что ряд стал стационарным.
Рис. 5.13. Исходный ряд после взятия первых и четвертых разностей
На этапе идентификации модели необходимо решить, как много параметров авторегрессии (p) и скользящего среднего (q) должно присутствовать в модели процесса. На практике часто число параметров p или q ограничивают значением 2.
В ходе анализа исходного ряда, была выявлена интервенция на 27 квартале из-за резкого спада внешнеторгового оборота России под влиянием мирового финансового кризиса. В связи с этим для прогнозирования экспорта России использовалась модельARIMA с постоянной устойчивой интервенцией в27 квартале.
Для нахождения качественной модели было проанализировано несколько комбинаций параметров (p,d,q)(P,D,Q). Среди адекватных моделей выбрана наиболее точная - модель ARIMA(0,1,0)(0,1,1), результаты которой представлены в табл. 5.14, 5.15и на рис.5.13.
Параметры модели прогноза объёмов экспорта
Таблица 5.14
| Исход.:Экспорт в час, млн. долл. США (Таблица0609.sta) Преобразования: ln(x),D(1),D(4) (Прерванная АРПСС) Модель(0,1,0)(0,1,1) Сезонный лаг: 4 MS Остаток= ,01318 | |||||||||
| Парам. | Асимпт. | Асимпт. | p | Нижняя | Верхняя | Интерв. | Интерв. | Асимпт. | |
| Qs(1) | 0,852619 | 0,093471 | 9,12176 | 0,000000 | 0,664472 | 1,040767 | |||
| Омега(1) | -0,223677 | 0,085869 | -2,60487 | 0,012338 | -0,396522 | -0,050832 | пост/уст | ||
| Дельта1) | 0,733754 | 0,116116 | 6,31914 | 0,000000 | 0,500024 | 0,967484 | пост/уст | -0,840114 |
Результаты прогноза объёмов экспорта
Таблица 5.15
| Номер квартала | Прогноз | Нижний 90% | Верхний 90% | Отношение значения верхней границы к нижней |
| 194,20 | 160,15 | 235,47 | 1,47 | |
| 211,55 | 161,07 | 277,84 | 1,72 | |
| 218,32 | 156,35 | 304,85 | 1,95 | |
| 226,30 | 153,91 | 332,74 | 2,16 |
Рис.5.14. Прогноз объёмов экспорта
Принято считать, что если отношение верхней границы прогноза к её нижней границе меньше двух, то прогноз считается достаточно точным. Как следует из данных таб. 5.15 упомянутое условие выполняется только для 55 и 56 кварталов, т.е. для 3-го и 4-го кварталов 2015 года.
Как видно из графика (рис.5.15), выборочная плотность распределения остатков достаточно хорошо аппроксимируется нормальным законом распределения, что является одним из признаков адекватности построенной модели.
Рис.5.15. Выборочная плотность распределения остатков
В результате анализа остатков установлено, что они практически не коррелированы, имеют равную вариацию на всем протяжении ряда (кроме 27 квартала) и нет очевидного тренда или сдвига их. Из графиков (рис.5.16,5.17) видно, что остатки практически являются белым шумом.

Рис.5.16. Автокорреляционная функция остатков
Рис.5.17. Частная автокорреляционная функция остатков
Соответствующие таблицы и графики по импорту приведены ниже.
Параметры модели прогноза объёмов импорта
Таблица 5.16
| Исход.:Импорт в час, млн. долл. США (Таблица0609.sta) Преобразования: ln(x),D(1),D(4) (Прерванная АРПСС) Модель(0,1,0)(0,1,1) Сезонный лаг: 4 MS Остаток= ,01030 | |||||||||
| Парам. | Асимпт. | Асимпт. | p | Нижняя | Верхняя | Интерв. | Интерв. | Асимпт. | |
| Qs(1) | 0,686282 | 0,260973 | 2,62971 | 0,011583 | 0,160971 | 1,211593 | |||
| Омега(1) | -0,217437 | 0,089076 | -2,44103 | 0,018553 | -0,396737 | -0,038137 | пост/уст | ||
| Дельта1) | 0,743828 | 0,084907 | 8,76053 | 0,000000 | 0,572919 | 0,914736 | пост/уст | -0,848790 |
Результаты прогноза объёмов импорта
Таблица 5.17
| Номер квартала | Прогноз | Нижний 90% | Верхний 90% | Отношение значения верхней границы к нижней |
| 95,65 | 80,66 | 113,41 | 1,41 | |
| 101,70 | 79,92 | 129,40 | 1,62 | |
| 85,50 | 63,65 | 114,84 | 1,80 | |
| 93,14 | 66,25 | 130,95 | 1,98 |
Рис.5.18. Прогноз объёмов импорта
Рис.5.19. Выборочная плотность распределения остатков
Рис.5.20. Автокорреляционная функция остатков
Рис.5.21.Частная автокорреляционная функция остатков
Таким образом, с доверительной вероятностью 0,9 объёмы экспорта и импорта в млрд. долларов США составят:
| Экспорт | ||||
| Номер квартала 2015 года | Прогноз | Нижний 90% | Верхний 90% | Отношение значения верхней границы к нижней |
| 102,54 | 84,56 | 124,33 | 1,47 | |
| 109,58 | 83,44 | 143,92 | 1,72 |
| Импорт | ||||
| Номер квартала 2015 года | Прогноз | Нижний 90% | Верхний 90% | Отношение значения верхней границы к нижней |
| 50,50 | 42,59 | 59,88 | 1,41 | |
| 52,68 | 41,40 | 67,03 | 1,62 |
КЛАСТЕРНЫЙ АНАЛИЗ
ОБЩАЯ ХАРАКТЕРИСТИКА ПРОЦЕДУР КЛАСТЕРИЗАЦИИ
Кластерный анализ и его роль в социально-экономических исследованиях.
При анализе и прогнозировании социально-экономических явлений исследователь довольно часто сталкивается с многомерностью их описания. Это происходит, например, при решении задач сегментирования рынка, построения типологии стран по достаточно большому числу показателей, прогнозирования конъюнктуры рынка отдельных товаров, изучения и прогнозирования экономической депрессии и многих других проблем.
Кластерный анализ — один из методов многомерной статистики — наиболее ярко отражает черты многомерности в процедуре классификации объектов. Название «кластерный анализ» происходит от английского слова «cluster» — гроздь, скопление. Впервые определил предмет кластерного анализа и дал его описание исследователь Трион (Тгуоп) в 1939 г. [3].
Главное назначение кластерного анализа — разбиение множества исследуемых объектов, характеризуемых совокупностью признаков*, на однородные в соответствующем понимании группы (кластеры). Это означает, что решается задача классификации данных и выявления соответствующей структуры в ней. Иными словами, предполагается выделение компактных, удаленных друг от друга групп объектов или отыскание «естественного» разбиения совокупности на области скопления.
Кластерный анализ является одним из направлений статистического исследования социально-экономических процессов, которые связаны с изучением массовых явлений.
Пример 3.1. Некая фирма собирается начать выпуск нового стирального порошка. Разработана анкета, содержащая ряд вопросов, характеризующих отношение респондентов к свойствам продукта. Респонденты должны проранжировать факторы по степени их значимости, начиная с самого важного, — от 1 до 8. Строгое определение понятий «объект» и «признак» будет дано в подпараграфе 3.1.2.
Результаты классификации объектов (респондентов) по переменным (свойствам продукта) представлены в табл. 3.1.
Таблица 3.1
Результаты классификации респондентов по предпочтениям
| Свойства продукта | Ранги свойств по сегментам | |||
| 1 (18%) | 2 (7%) | 3 (60%) | 4 (15%) | |
| Моющая способность | ||||
| Отдушка | ||||
| Цена | ||||
| Безвредность | ||||
| Эффект отбеливания | ||||
| Подсинивание | ||||
| Быстрое растворение | ||||
| Отсутствие пыления |
Получилось четыре сегмента, существенно различающиеся между собой по наиболее важным признакам продукта. Эти признаки выделены в таблице. Их можно назвать «сегментообразующими». Легко видеть, что сегмент 3 — самый крупный (60% от выборки). Это прагматики, для которых важнейшей характеристикой продукта является его цена, а также такие качества, как моющая способность и эффект отбеливания. В следующем по величине сегменте 1, напротив, на первом месте стоит безвредность порошка, цена же занимает последнее место.
Далее может проводиться сегментация по вопросам, касающимся, например, стиля поведения респондентов («покупаю дешевые», «пользуюсь новинками» и т.п.).
Таким образом, результаты кластерного анализа фактически опишут портрет потребителя с рациональной (свойства стирального порошка) и эмоциональной (оценка степени согласия с утверждениями) точек зрения. На основе их можно определить целевую группу качеств, расставить акценты в рекламном сообщении, избавиться от иллюзий относительно исключительности своего товара по какому-либо определенному свойству и т.д.
Большое достоинство кластерного анализа в том, что он позволяет выполнить разбиение объектов не по одному параметру, а по целому набору признаков. Кроме того, кластерный анализ, в отличие от большинства математико-статистических методов, не накладывает никаких ограничений на вид изучаемых объектов и позволяет рассматривать множество исходных данных практически произвольной природы. Это имеет большое значение, например, для прогнозирования конъюнктуры рынка, когда показатели весьма разнообразны и затруднительно применение традиционных эконометрических подходов.
Кластерный анализ играет важную роль и для совокупностей временных рядов, характеризующих экономическое развитие. В частности, можно выделить периоды, когда значения соответствующих показателей были достаточно близкими, а также определить группы показателей, динамика которых во времени наиболее схожа.
Необходимость развития и использования методов кластерного анализа продиктована прежде всего тем, что они помогают построить научно обоснованные классификации, выявить внутренние связи между единицами наблюдаемой совокупности. Построение классификаций особенно актуально для слабоизученных явлений, когда необходимо установить наличие связей внутри совокупности и попытаться привнести в нее структуру.
Методы кластерного анализа могут применяться с целью сжатия информации, в условиях постоянного увеличения и усложнения потоков статистических данных. При этом в задачах социально- экономического прогнозирования весьма перспективно сочетание кластерного анализа с другими количественными методами (с корреляционно-регрессионным, факторным анализом и т.п.).
Как и любой другой метод, кластерный анализ имеет определенные недостатки и ограничения. Так, состав и количество кластеров зависит от выбираемых критериев разбиения. При сведении исходного массива данных к более компактному виду могут возникнуть определенные скажения, а также потеряться индивидуальные черты отдельных объектов за счет замены их характеристик обобщенными значениями параметров кластера.
3.1.2. Расстояния между объектами и кластерами
Различия между схемами решения задач классификации во многом определяются тем, что понимают под сходством, однородностью объектов.
Введем вначале такие ключевые для данной главы понятия, как объект и признак.
Под объектами будем подразумевать конкретные предметы исследования, нуждающиеся в классификации. Такими объектами могут быть, например, потребители продукции, отличающиеся своими предпочтениями, различные регионы или страны, предприятия, их продукция и т.п.
Признак (синонимы: свойство, переменная, характеристика) представляет собой конкретное свойство объекта.
Различные свойства могут выражаться как числовыми, так и нечисловыми значениями. Например, объем производства может измеряться в килограммах или тоннах, цена жилья — в тысячах рублей (долларов) и т.п. Такие признаки называются количественными (непрерывными). Над ними можно производить арифметические операции.
В отличие от числовых характеристик ряд признаков может иметь дискретные, прерывистые значения. В свою очередь, дискретные признаки делятся на две группы. Первая группа — порядковые (ранговые) переменные. Таким признакам присуще свойство упорядоченности значений. К ним можно отнести возраст, этаж дома, год выпуска и др. Значения ранговых переменных представляются натуральными числами. Вторая группа дискретных признаков не имеет такой упорядоченности и носит название номинальных переменных. Это переменные, принимающие два значения (дихотомические) или более. Этим значениям можно поставить в соответствие некоторые числа, которые, однако, не будут отражать какой-либо упорядоченности значений переменной. Примером таких признаков может быть пол респондента, тип дома, вид транспортного средства и т.п. Эти признаки относятся к шкале наименований. Их можно считать качественными характеристиками объектов.
Обычной формой представления исходных данных в задачах кластерного анализа служит прямоугольная таблица «объект — признак»
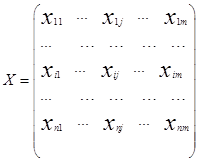
каждая строка которой представляет результат измерений m рассматриваемых признаков на одном из n обследованных объектов.
Пример 3.2. Пусть имеется 13 объектов, у которых измерено два признаками Y(табл. 3.2).
Таблица 3.2
Совокупность объектов с двумя признаками
| Испытуемый | Признак X | Признак Y |
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F | ||
| G | ||
| H | ||
| I | ||
| J | ||
| K | ||
| L | ||
| M |
Непосредственная инспекция таблицы данных не позволяет увидеть то, что является очевидным, но после построения диаграммы рассеяния (рис. 3.1) совокупность объектов распадается на три хорошо различимые группы.
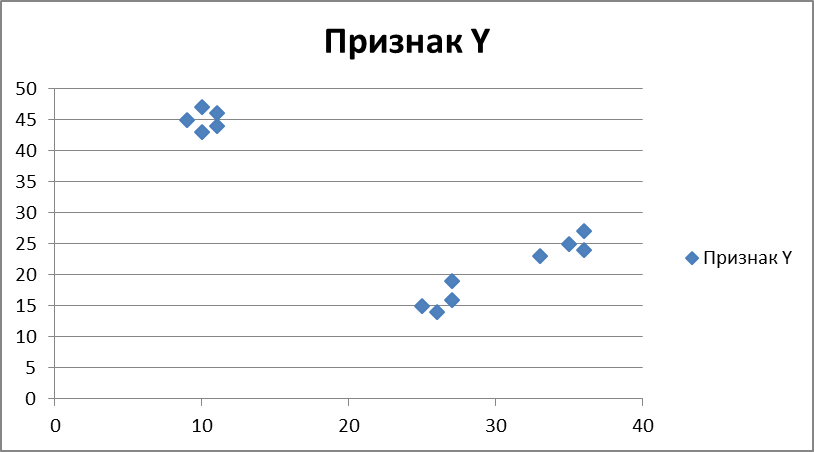

Рис. 3.1. Диаграмма рассеяния
Объекты внутри кластера более «похожи» друг на друга, чем на объекты из других групп. Таким образом, кластерный анализ ориентирован на выделение некоторых геометрически удаленных групп, внутри которых объекты близки.
В кластерном анализе для количественной оценки сходства вводится понятие «расстояние между объектами». Кроме термина «расстояние» в литературе часто встречаются и другие термины — «метрика», «мера», которые подразумевают метод вычисления того или иного конкретного расстояния.
Если каждый объект описывается т признаками, то он может быть представлен как точка в m-мерном пространстве, и сходство с другими объектами будет определяться как соответствующее расстояние.
Расстоянием между i-м и j-м объектами в пространстве признаков называется такая величина 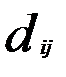 , которая удовлетворяет следующим аксиомам:
, которая удовлетворяет следующим аксиомам:
1) 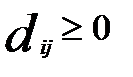 (неотрицательность);
(неотрицательность);
2) 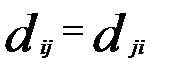 (симметрия);
(симметрия);
3) 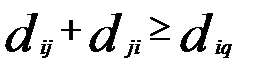 (неравенство треугольника, здесь q — номер объекта);
(неравенство треугольника, здесь q — номер объекта);
4) если 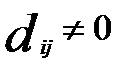 , то
, то 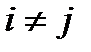 (различимость нетождественных объектов);
(различимость нетождественных объектов);
5) если 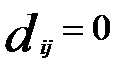 , то
, то 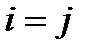 (неразличимость тождественных объектов).
(неразличимость тождественных объектов).
Меру близости (сходства) объектов удобно представить как величину, обратную расстоянию между объектами.
В многочисленных изданиях, посвященных кластерному анализу, описано более 50 различных способов вычисления расстояния между объектами. Выбор расстояния является узловым моментом исследования. От него во многом зависит окончательный вариант разбиения объектов на классы при данном алгоритме. Чаще других используются следующие меры расстояния между объектами:
1) евклидово расстояние
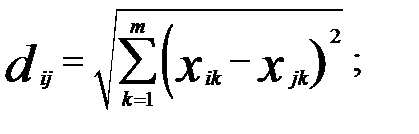
2) взвешенное евклидово расстояние
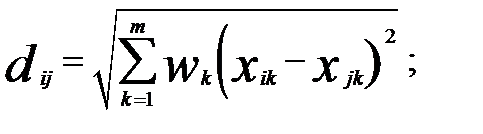
3) расстояние Миньковского
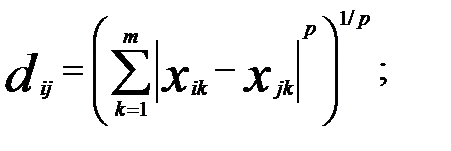
4) расстояние city-block (расстояние городских кварталов)
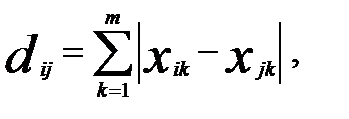
где 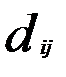 — расстояние между i-м и j-м объектами;
— расстояние между i-м и j-м объектами;
m — число переменных (признаков), которыми описываются объекты;
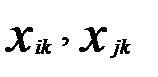 — значения k- й переменной соответственно у i-го и j-го объектов;
— значения k- й переменной соответственно у i-го и j-го объектов;
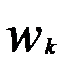 — вес, приписываемый к-й переменной, пропорциональный степени важности признака в задаче классификации;
— вес, приписываемый к-й переменной, пропорциональный степени важности признака в задаче классификации;
p — показатель степени, определяемый исследователем.
Дадим несколько комментариев к приведенным выше мерам расстояний между объектами.
Евклидово расстояние — одно из наиболее известных расстояний, которое доступно для восприятия и понимания в случае количественных признаков. Часто применяется также квадратичное евклидово расстояние, равное квадрату 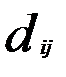 .
.
В ряде случаев используется взвешенное евклидово расстояние, при вычислении которого учитываются весовые коэффициенты 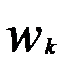 , придающие отдельным слагаемым в сумме большую значимость.
, придающие отдельным слагаемым в сумме большую значимость.
Весьма напоминает выражение для евклидова расстояния так называемое обобщенное степенное расстояние Минковского, в котором в степенях вместо двойки используется другая величина. В общем случае эта величина обозначается символом р. При р = 2 получаем обычное евклидово расстояние. Выбор конкретного значения степенного показателя р осуществляется самим исследователем.
Частным случаем расстояния Минковского является так называемое Хеммингово расстояние, или расстояние городских кварталов (city-block), соответствующее р= 1. Это расстояние широко используется для дихотомических (имеющих всего два значения) качественных признаков, относящихся к номинальной шкале. В этом случае оно равно числу несовпадений значений соответствующих признаков для рассматриваемых i-го и j-rо объектов.
Как видно, метрика Миньковского фактически представляет собой большое семейство метрик, включающее и наиболее популярные.
Однако существуют и принципиально отличающиеся от метрик Минковского методы вычисления расстояния между объектами. Так, расстояние Махаланобиса имеет достаточно специфические свойства. Оно связано с корреляциями переменных. Когда корреляции между переменными равны нулю, расстояние Махаланобиса эквивалентно квадрату евклидова расстояния.
В более широком смысле под объектами можно понимать не только исходные предметы исследования, представленные в матрице «объект — признак» в виде отдельной строки или отдельными точками в многомерном признаковом пространстве, но и отдельные группы таких точек, объединенные тем или иным алгоритмом в кластер. В этом случае возникает вопрос: что понимать под расстоянием между такими скоплениями точек (кластерами) и как его вычислять? Иными словами, необходимо определить правила вычисления расстояния между группами объектов или меры близости (сходства) двух групп объектов (в отличие от меры расстояния между объектами), которые будут важны при объединении кластеров.
Отметим, что для определения расстояний между кластерами разнообразных возможностей еще больше, нежели при вычислении расстояния между двумя наблюдениями в многомерном пространстве. Эта процедура осложняется тем, что в отличие от точек кластеры занимают определенный объем многомерного пространства, имеют протяженность и состоят из многих точек.
Мера сходства для объединения кластеров может быть определена различными:
• методом «ближнего соседа» — степень сходства оценивается по расстоянию между ближайшими объектами кластеров;
• методом «дальнего соседа» — степень сходства оценивается по расстоянию между наиболее отдаленными объектами кластеров;
• центроидным методом — расстояние между кластерами определяется расстоянием между их центрами тяжести;
• методом средней связи — расстояние определяется как среднее арифметическое всех попарных расстояний между представителями рассматриваемых групп.
Использование различных мер сходства для объединения объектов (кластеров) приводит к различным кластерным структурам и влияет на качество кластеризации. Поэтому соответствующая мера должна выбираться с учетом имеющихся сведений о существующей структуре совокупности объектов.
3.1.3. Анализ качества классификации
Кластерный анализ приводит к разбиению на кластеры с учетом всех группировочных признаков одновременно. При этом, как правило, не указаны четкие границы каждой группы, а также неизвестно заранее, сколько групп целесообразно выделить в исследуемой совокупности.
С целью сравнительного анализа качества различных способов разбиения в кластерном анализе вводится понятие функционала качества разбиения Q(S). Многие методы кластеризации различаются тем, что их алгоритмы на каждом шаге вычисляют разнообразные функционалы качества разбиения. Решение экстремальных задач позволяет определить количественный критерий, следуя которому можно было бы предпочесть одно разбиение другому. При выборе количественного показателя качества разбиения исходят подчас из эмпирических соображений.
Под наилучшим разбиением понимают то, на котором достигается экстремум (минимум или максимум) выбранного функционала качества.
Пусть исследователем выбрана метрика d в пространстве X наблюдений (объектов) 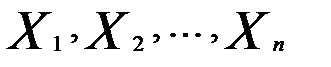 и
и 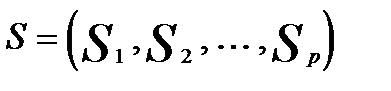 — некоторое фиксированное разбиение объектов на заданное число р классов
— некоторое фиксированное разбиение объектов на заданное число р классов 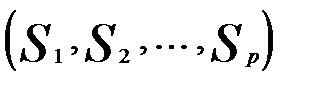 .
.
Наиболее распространены следующие характеристики функционала качества:
• сумма внутриклассовых дисперсий расстояний
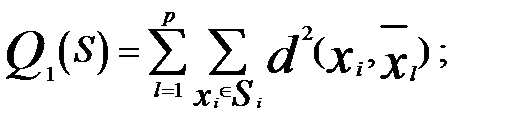
• сумма попарных внутриклассовых расстояний между внутри кластерными элементами
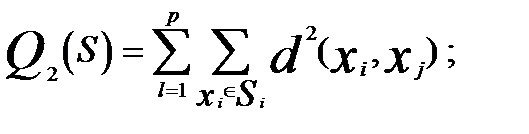
где 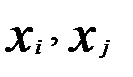 — многомерные переменные, характеризующие соответственно объекты
— многомерные переменные, характеризующие соответственно объекты 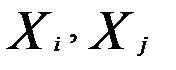 ;
;
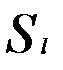 — некоторый фиксированный кластер;
— некоторый фиксированный кластер;
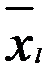 — среднее значение многомерной переменной
— среднее значение многомерной переменной 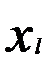 , вычисленное по наблюдениям
, вычисленное по наблюдениям 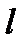 -г о кластера (центр
-г о кластера (центр 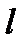 -го кластера). Судить о качестве разбиения позволяют и некоторые простейшие приемы. Например, сравнение средних значений признаков в отдельных группах со средними значениями в целом по всей совокупности объектов. Если отличие групповых средних от общего среднего значения существенное (для проверки существенности применяется t-критерий Стьюдента), то это является признаком хорошего разбиения.
-го кластера). Судить о качестве разбиения позволяют и некоторые простейшие приемы. Например, сравнение средних значений признаков в отдельных группах со средними значениями в целом по всей совокупности объектов. Если отличие групповых средних от общего среднего значения существенное (для проверки существенности применяется t-критерий Стьюдента), то это является признаком хорошего разбиения.
Перечисленные способы оценки качества разбиения предполагают формальный подход и являются для исследователя только вспомогательными средствами. Основная роль принадлежит содержательному анализу результатов классификации.
Выбрать лучший вариант разбиения легче, если провести подготовительную работу. К подготовительному этапу относят, прежде всего, выбор признаков, характеризующих классифицируемые объекты. На начальном этапе желательно также определить критерии качества, отвечающие условию задачи, или целевую функцию, значения которой позволят сопоставить различные схемы классификации. В экономических исследованиях целевая функция, как правило, должна оптимизировать некий параметр, определенный на множестве объектов (например, максимизировать прибыль, минимизировать затраты и т.п.).
В тех случаях, когда формализовать цель задачи не удается, критерием качества классификации может служить возможность содержательной интерпретации найденных групп, например, в результате определения кластерных профилей.
Пример 3.3. Допустим, проведено анкетирование сотрудников некой компании и нужно определить, каким образом можно наиболее эффективно управлять персоналом, т.е. необходимо разделить сотрудников на группы и для каждой из них выделить наиболее эффективные рычаги управления. При этом различия между группами должны быть очевидными, а респонденты внутри группы будут максимально похожи. Не вдаваясь пока в подробности процедуры кластеризации, рассмотрим результирующую таблицу кластерных профилей (табл. 3.3).
Таблица 3.3
Кластерные профили
В первом столбце таблицы находится номер кластера, данные по которому отражены в строке. Например, первый кластер на 80% составляют мужчины, 90% попадают в возрастную категорию от 30 до 50 лет, а 12% респондентов считают, что льготы очень важны.
Составим теперь портреты респондентов каждого кластера.
Первая группа — в основном мужчины зрелого возраста, занимающие руководящие позиции. Соцпакет (медицинское обслуживание и льготы) их не интересует. Они предпочитают получать хорошую зарплату, а не помощь от работодателя.
Вторая группа, наоборот, отдает предпочтение соцпакету. Состоит она в основном из людей в возрасте, занимающих невысокие посты. Зарплата для них, безусловно, важна, но есть и другие приоритеты.
Третья группа наиболее «молодая». Здесь очевиден интерес к возможностям обучения и профессионального роста. У этой категории есть хороший шанс в скором времени пополнить первую группу.
Таким образом, планируя кампанию по внедрению эффективных методов управления персоналом, можно увеличить соцпакет у второй группы в ущерб зарплате. Специалистам из третьей группы можно рекомендовать пройти обучение.
В зависимости от количества признаков, их взаимосвязи, выбранного критерия качества определяется наиболее подходящий алгоритм классификации. Все это облегчает последующую интерпретацию результатов разбиения и позволяет судить о его качестве с точки зрения поставленной задачи.
В целом различают три подхода к проблеме кластерного анализа:
• эвристический — характеризуется отсутствием формальной модели для сравнения различных решений; алгоритм строится, исходя из интуитивных соображений;
• экстремальный — задается критерий, определяющий качество разбиения на кластеры;
• статистический — задача кластерного анализа решается на основе вероятностной модели исследуемого процесса. Существуют визуальные способы исследования результатов
кластеризации. Они связаны прежде всего со свойствами кластеров. Обсудим наиболее важные из них.
1. Плотность распределения наблюдений внутри кластера. Это свойство дает нам возможность определить, насколько данный кластер является «заполненным», или же наоборот — разреженным. Несмотря на очевидность этого свойства, однозначного способа вычисления плотности кластера не существует. Наиболее удачным показателем, характеризующим компактность, плотность «упаковки» многомерных наблюдений, является дисперсия расстояния от центра кластера до отдельных его точек. Чем меньше дисперсия этого расстояния, тем ближе к центру кластера находятся наблюдения, тем больше плотность кластера. И наоборот, чем больше дисперсия расстояния, тем более разрежен данный кластер и, следовательно, есть точки, находящиеся как вблизи центра кластера, так и достаточно далеко от его центра.
2. Размер кластера. Основным показателем размера кластера является его «радиус». Это свойство наиболее полно отражает фактический размер кластера, если рассматриваемый кластер имеет круглую форму или является гиперсферой в многомерном пространстве. Однако если кластеры имеют удлиненные формы, радиус или диаметр уже не отражает их истинного размера.
3. Локальность, отделимость кластеров. Это свойство характеризует степень перекрытия и взаимной удаленности кластеров друг от друга в многомерном пространстве. В частности, используя данное свойство, можно в дальнейшем рассмотреть вопросы о целесообразности объединения наиболее близких кластеров или их перекрывающихся частей, об отделении от кластера элементов, больше других удаленных от его центра, и пр.
Таким образом, кластерный анализ — это не только формализуемая процедура; в нем всегда есть место наблюдению, интуиции, искусству и творчеству исследователя.
3.1.4. Методы кластерного анализа
Из всех методов кластерного анализа наиболее распространенными являются иерархические агломеративные методы. Сущность их заключается в следующем. На первом шаге каждый объект выборки рассматривается как отдельный кластер. Процесс объединения кластеров происходит последовательно: на основе матрицы расстояний (или матрицы сходства) 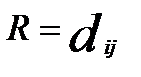 , где
, где 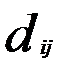 — расстояние между i-м и j-м объектами, объединяются наиболее близкие объекты.
— расстояние между i-м и j-м объектами, объединяются наиболее близкие объекты.
Последовательность объединения легко поддается геометрической интерпретации и может быть представлена в виде дендрограммы (рис. 3.4). На вертикальной оси отмечается расстояние, на котором объединялись объекты или кластеры. Процесс прекращают, когда объединяются кластеры, находящиеся на большом расстоянии друг от друга.
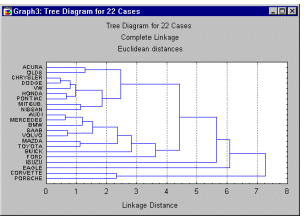
Рис. 3.4. Пример дендрограммы иерархического агломеративного кластерного анализа
Методы иерархического агломеративного кластерного анализа различаются не только используемыми мерами сходства (см. подпараграф 3.1.2), но и алгоритмами классификации. Наиболее распространенными из них являются следующие методы:
• одиночной связи;
• полных связей;
• средней связи;
• Уорда.
В методе одиночной связи объект будет присоединен к уже существующему кластеру, если хотя бы один из элементов кластера имеет тот же уровень сходства, что и присоединяемый объект. Отсюда и название метода — «одиночная (или единственная) связь».
Для метода полных связей присоединение объекта к кластеру происходит лишь в том случае, когда сходство между кандидатом на включение и любым из элементов кластера не меньше некоторого порога.
Метод средней связи имеет несколько модификаций, которые являются некоторым компромиссом между одиночной и полной связью. В них вычисляется среднее значение сходства кандидата на включение со всеми объектами существующего кластера. Присоединение происходит в том случае, когда найденное среднее значение сходства достигает или превышает некоторый порог. Наиболее часто используют среднее арифметическое сходство между объектами кластера и кандидата на включение в кластер.
Популярный метод Уорда построен таким образом, чтобы оптимизировать минимальную дисперсию внутрикластерных расстояний. На первом шаге каждый кластер состоит из одного объекта, в силу чего внутри кластерная дисперсия расстояний равна нулю. Объединяются те объекты, которые дают минимальное приращение дисперсии, вследствие чего данный метод имеет тенденцию к порождению гиперсферических кластеров.
Приведем пример агломеративного иерархического алгоритма.
Пример 3.4. Требуется провести классификацию шести регионов по двум заданным признакам. Исходные данные по материалам Российского статистического ежегодника [33], раздел «Отраслевая структура промышленного производства по регионам Российской Федерации в 2003 году», представлены в табл. 3.4.
Таблица 3.4
Отраслевая структура промышленного производства (фрагмент)
| № п/п | Область | Объём промышленного производства, % | |
| электроэнергетика | машиностроение | ||
| Липецкая | 6,9 | 11,5 | |
| Тульская | 11,1 | 20,1 | |
| Тамбовская | 21,3 | 34,2 | |
| Воронежская | 20,5 | 22,1 | |
| Белгородская | 9,7 | 13,4 | |
| Брянская | 18,2 | 29,4 |
Решение. Воспользуемся меню графиков в SPSS и представим две заданные переменные в виде простой диаграммы рассеяния (рис. 3.5), на которой отчетливо видны две группы точек.
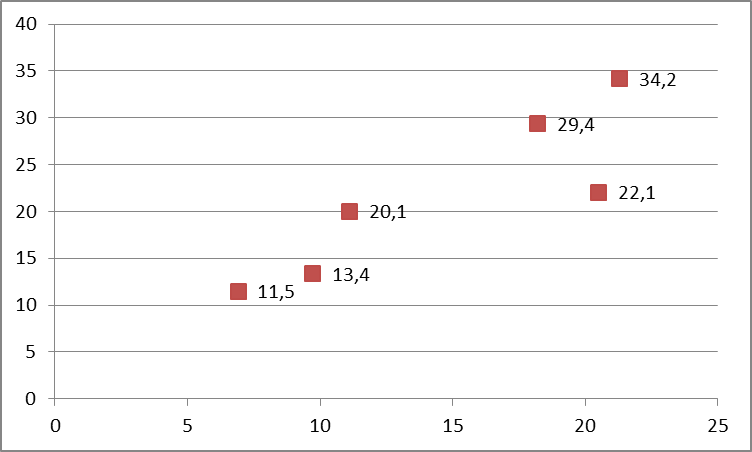

Следовательно, шесть данных областей явно распадаются на два различных кластера.
Воспользуемся теперь агломеративным иерархическим алгоритмом классификации. В качестве расстояния между объектами возьмём обычное евклидовое расстояние. Тогда расстояние между первым и вторым объектами
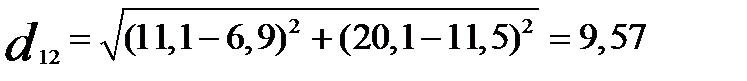 ,
,
Между первым и третьим
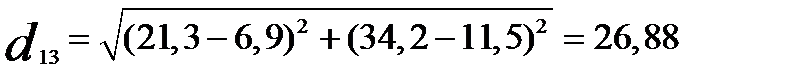 .
.
Очевидно, что 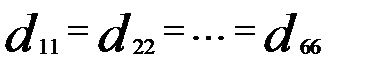 .
.
Аналогично находим все остальные расстояния между шестью объектами и строим матрицу расстояний:

Из матрицы расстояний следует, что первый и пятый объекты наиболее близки ( 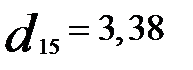 ), поэтому они объединяются в один кластер.
), поэтому они объединяются в один кластер.
После первого объединения имеем пять кластеров:
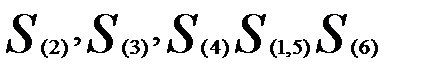 .
.
Расстояние между кластерами определим по принципу «ближайшего соседа». Так, расстояние между кластерами 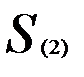 и
и 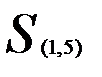 определяется равенством
определяется равенством
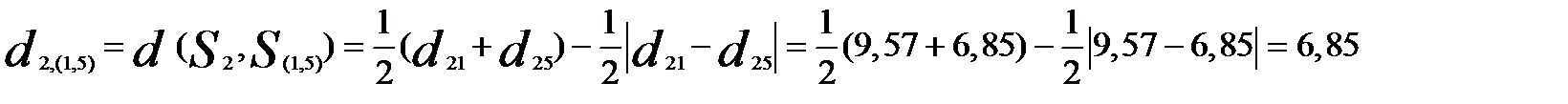
Таким образом, расстояние 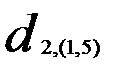 равно расстоянию от второго объекта до ближайшего к нему объекта, входящего в кластер
равно расстоянию от второго объекта до ближайшего к нему объекта, входящего в кластер 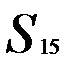 , т.е.
, т.е. 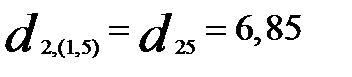 . Тогда матрица расстояний примет вид
. Тогда матрица расстояний примет вид

Объединяем теперь третий и шестой объекты, имеющие наименьшее расстояние 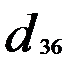 . После объединения имеем четыре кластера:
. После объединения имеем четыре кластера:
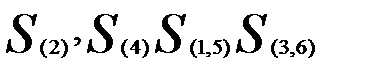
Вновь найдем матрицу расстояний. Для того чтобы рассчитать расстояние до кластера £(| 5), воспользуемся матрицей расстояний 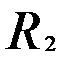 . Например, расстояние между кластерами
. Например, расстояние между кластерами 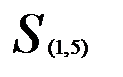 и
и 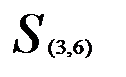
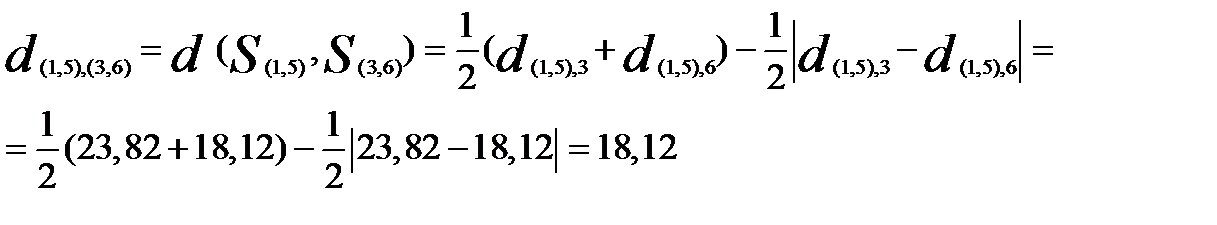
В результате получим новую матрицу расстояний
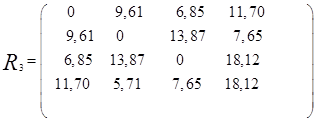
Теперь объединяем кластеры 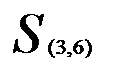 и
и 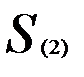 (
( 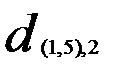 = 6,85 — наименьшее). В результате получим три кластера:
= 6,85 — наименьшее). В результате получим три кластера:
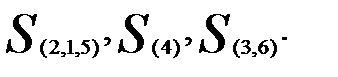
Так как
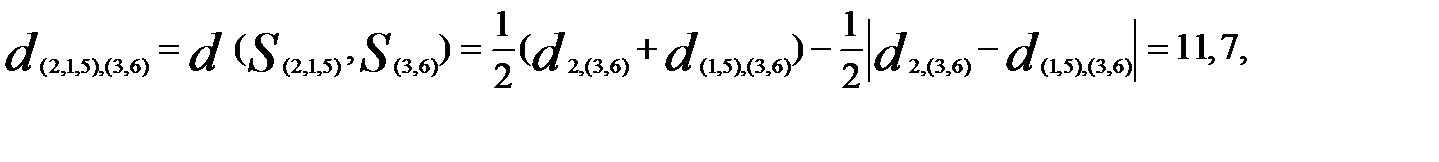
то новая матрица расстояний будет иметь вид
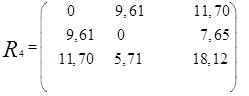
Объединяем теперь кластеры 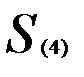 и
и 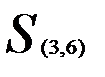 (
( 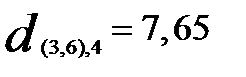 — наименьшее). В результате получаем два кластера
— наименьшее). В результате получаем два кластера 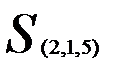 ,
, 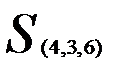 расстояние между которыми, найденное по принципу «ближайшего соседа»,
расстояние между которыми, найденное по принципу «ближайшего соседа»,
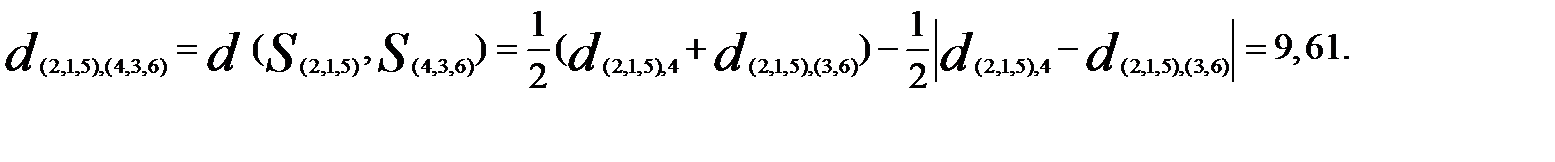
Тогда
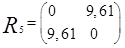
Таким образом, последнее объединение произойдет на расстоянии 9,61.
Иерархические дивизимные методы противоположны агломеративным по логическому построению процедур классификации. Исходной посылкой дивизимных методов является то, что первоначально все объекты принадлежат одному кластеру. В процессе классификации от этого кластера отделяются группы схожих между собой объектов. Таким образом, на каждом шаге количество кластеров возрастает, а мера расстояния между ними уменьшается.
Пример 3.5. Пусть дана матрица расстояний между пятью объектами Х1, ..., Х5
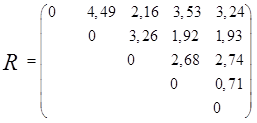
Требуется провести классификацию по дивизимному алгоритму.
Решение. Наиболее удаленными являются объекты X1 и Х2
( 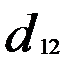 = 4,49); оценим расстояния оставшихся объектов до первого и
= 4,49); оценим расстояния оставшихся объектов до первого и
второго:
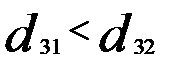 — объект X3 ближе к Х1;
— объект X3 ближе к Х1;
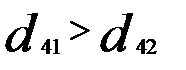 — объект Х4 ближе к Х2;
— объект Х4 ближе к Х2;
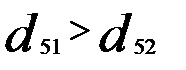 — объект Х5 ближе к Х2.
— объект Х5 ближе к Х2.
Таким образом, получаем два кластера: 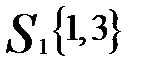 и
и 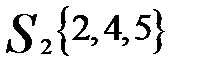 . В каждом из них анализируем расстояния между объектами, и на очередном шаге происходит разделение того кластера, где достигается максимум расстояния между объектами:
. В каждом из них анализируем расстояния между объектами, и на очередном шаге происходит разделение того кластера, где достигается максимум расстояния между объектами:
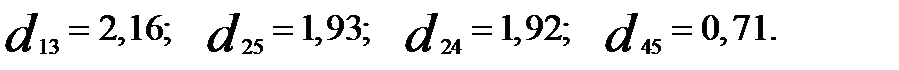
Наибольшее расстояние 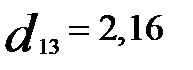 , следовательно, объекты Х1 и Х3 выделяем в отдельные кластеры. В кластере
, следовательно, объекты Х1 и Х3 выделяем в отдельные кластеры. В кластере 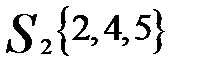 ищем максимальное расстояние max{d24, d25, d45} = 1,93. На следующем шаге из этого кластера выделяем объект X2 и, наконец, на последнем шаге разделяем кластер 5
ищем максимальное расстояние max{d24, d25, d45} = 1,93. На следующем шаге из этого кластера выделяем объект X2 и, наконец, на последнем шаге разделяем кластер 5 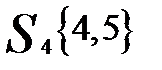 на два кластера на расстоянии 0,71.
на два кластера на расстоянии 0,71.
Из этого примера видно, что дивизимный алгоритм не требует пересчета матрицы расстояний на каждом шаге классификации, в отличие от агломератавных методов.
Сущность итеративных методов кластерного анализа заключается в том, что процесс классификации начинается с задания некоторых начальных условий (количество образуемых кластеров, порог завершения процесса классификации и др.). Итеративные методы в большей степени, чем иерархические, требуют от пользователя интуиции при выборе типа классификационных процедур и задании начальных условий разбиения, так как большинство этих методов очень чувствительны к изменению задаваемых параметров. В отличие от иерархических методов итеративные алгоритмы могут привести к образованию пересекающихся кластеров, когда один объект может одновременно принадлежать нескольким кластерам.
Примером итеративной кластеризации может служить метод k-средних. Алгоритм метода k-средних (впрочем, как и иерархический агломеративный метод Уорда) основан на принципе минимизации внутрикластерной дисперсии (см. подпараграф 3.1.3).
Метод k-средних принадлежит к группе итеративных методов эталонного типа. Название метода было предложено Дж. МакКуином в 1967 г. Этот метод удобен для обработки больших статистических совокупностей.
После того как принято волевое решение о числе разбиений, алгоритм k-средних начинает свою работу с того, что случайным образом в пространстве назначает центры будущих кластеров. Затем вычисляется расстояние между центрами кластеров и каждым объектом, и объект приписывается к тому кластеру, к которому он ближе всего. Завершив приписывание, алгоритм вычисляет средние значения для каждого кластера. Набор средних представляет собой координаты нового положения центра кластера. Алгоритм вычисляет расстояние от каждого объекта до центров кластеров и приписывает объекты к ближайшему кластеру. Вновь вычисляются центры тяжести, и этот процесс повторяется до тех пор, пока центры тяжести не перестанут «мигрировать» в пространстве.
Процедуры кластеризации почти всегда сопряжены с трудоемкими расчетами, поэтому для реализации соответствующих алгоритмов применяются пакеты специальных прикладных программ.
[1] Прогнозирование с помощью моделей ARIMAсм. в кн. :Дуброва Т. А.Статистические методы прогнозирования. М.: ЮНИТИ, 2003. С. 178—184.
Дата добавления: 2016-03-22; просмотров: 4218;
