Временные ряды с использованием процесса скользящего среднего могут иметь место, когда уровни динамического ряда характеризуются случайной колеблемостью.
Модели ARMA
Соединение в одной модели авторегрессионного процесса ARи модели скользящего среднего МА приводит к модели авторегрессионного процесса со скользящими средними в остатках
(ARMА — отанглийскогоAuto Regressive — Moving Average):
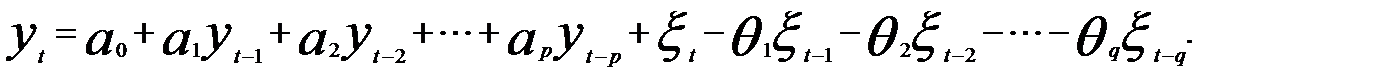(5.65)
В модели (7) в качестве объясняющих переменных рассматриваются лаговые значения зависимой переменной с р интервалами сдвига и скользящие средние порядка q для остатков авторегрессии. Иными словами, модель включает в себя AR (р) и МА (q). Ее принято обозначать ARMA (р,q). Например, ARMA (3, 2) имеет вид
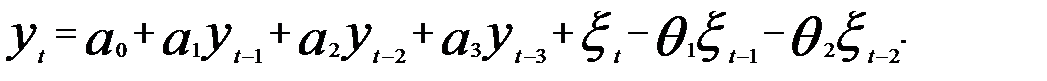(5.66)
При практической реализации моделей ARMA наиболее сложным является выбор числа лагов р и q.
Инструментом идентификации модели ARMA является изучение частной автокорреляционной функции по моделям с разным числом лагов. Частная автокорреляционная функция (PACF — PartialAutocorrelationFunction) представляет собой серию частных коэффициентов автокорреляции (РАС), которые измеряют связь между текущим уровнем динамического ряда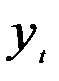 
и предыдущими значениями 
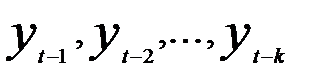в условиях, когда влияние других промежуточных временных лагов устранено. Так, частный коэффициент автокорреляции при лаге k будет представлять собой корреляцию 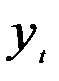и 
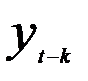,очищенную от влияния 
.
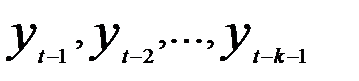Обозначим частный коэффициент автокорреляции с лагом kчерез ρ(k). При k = 0 ρ(0) = 1 (уровни ряда коррелируют сами с собой); при k = 1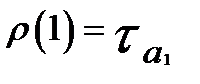 
, где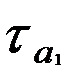 
— коэффициент автокорреляции первого порядка. Это равенство связано с тем, что при расчете ρ(1) отсутствуют промежуточные лаги. Вычисление ρболее высокого порядка можно производить по формулам
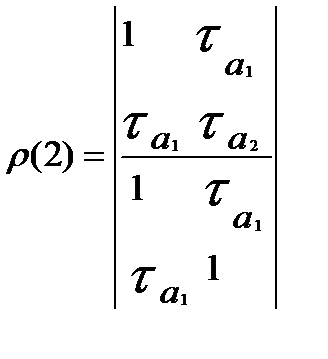
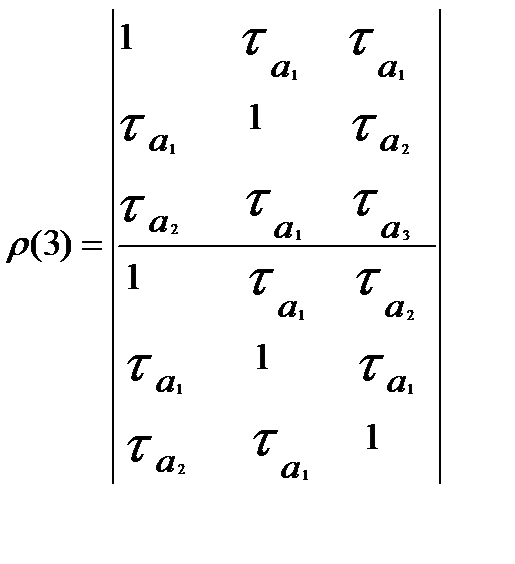
Для авторегрессионного процесса порядка ρ частная автокорреляционная функция отлична от нуля при k ≤ ρ и равна нулю при k>ρ. Это и позволяет определять порядок ρ процесса AR. Так, для модели AR (1):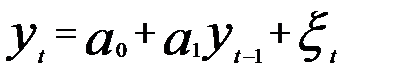 
ρ(2) близко к нулю.
Для модели типа МА (q) порядок q определяется по поведению автокорреляционной функции: при k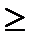 
рrа стремится к нулю. Для модели ARMA (р, q) автокорреляционная функция характеризуется убыванием, начинающимся с лага q, а частная автокорреляционная функция убывает, начиная с лага ρ. Так, для модели ARMA (1,1) при 
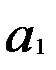> 0 ACF наблюдает экспоненциальное затухание с лага 1, aPACF — осциллирующее убывание с лага 1. При 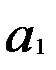<0 ACF для модели ARMA (1,1) наблюдает осциллирующее убывание с лага 1, aPACF — экспоненциальное затухание с лага 1.
Модели ARIMA
Дляполучения стационарного ряда могут рассчитываться разности уровней временного ряда ∆ разного порядка d. Модель, в которой соединены нахождение последовательных разностей временного ряда порядка d и ARMA, — модель порядка (р, q), получила название авторегрессионной интегрированной модели скользящей средней—ARIMA(AutoregressiveIntegratedMovingAverage).
Модель ARIMA обладает тремя параметрами: р — порядок авторегрессии AR; d — порядок последовательных разностей уровней временных рядов, обеспечивающий стационарность ряда, и q — порядок скользящей средней МА.
В общем виде модель ARIMA (р, d, q) выражается формулой
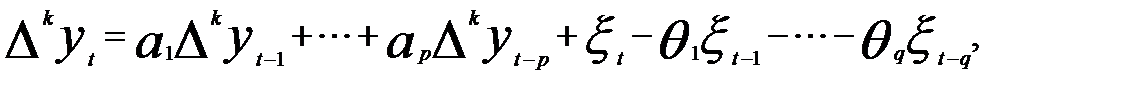(5.67)
где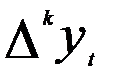 
— k-я последовательная разность уровней 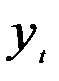, т.е. 
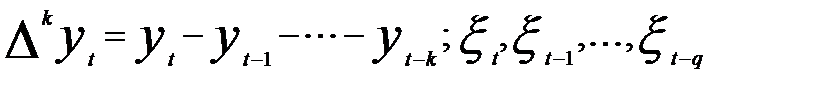— нормально распределенные случайные величины с нулевым математическим ожиданием и постоянной дисперсией.
Из модели (5.67) для 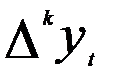можно получить модель для исходного динамического ряда с помощью выражения:
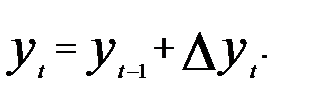(5.68)
Так, если модель ARIMA(1, 1, 1) имеет вид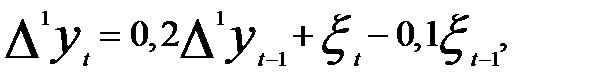 
то динамический ряд описывается моделью
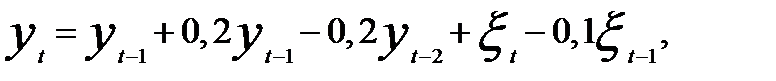
так как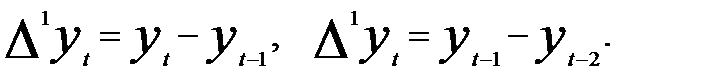 
Модель ARIMA практически пригодна для большинства временных рядов. При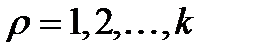 
d = 0 и q = 0 модель AR1MAпревращается в процесс AR
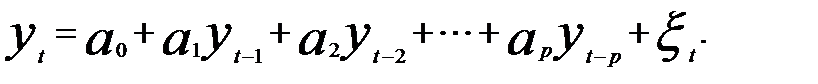
Если р = 0 , d = 0 и q = 1,2,…,k, то имеем модель МА
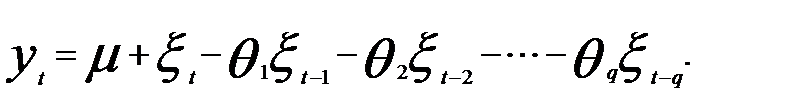
Наиболее распространены модели ARIMA с параметрами р, dи q, не превышающими двух. Современные компьютерные программы предлагают разные варианты оценивания параметров модели ARIMA, среди которых преобладает оценка методом максимального правдоподобия. Такой подход можно видеть при реализации модели ARIMA в системе SPSS[1].
Дата добавления: 2016-03-22; просмотров: 1156;