Инструментальные переменные как метод оценивания параметров модели авторегрессии
В силу того, что в модели авторегрессии в правой части содержатся лаговые эндогенные переменные, принято считать, что оценка параметров традиционным МНК дает неудовлетворительные результаты.
Предположим, что рассматривается модель авторегрессии вида (5.51).
Применение для оценивания параметров это уравнения традиционного МНК возможно, если выполняется предпосылка МНК относительно отсутствия автокорреляции остатков. Между тем при наличии в правой части лаговой зависимой переменной может иметь место автокорреляция остатков. Кроме того, может иметь место и зависимость объясняющей переменной 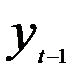 с остатками
с остатками 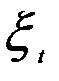 т.е. нарушается предпосылка о гомоскедастичности остатков. В силу этого классический МНК в случае малых выборок даст смещенные оценки параметров.
т.е. нарушается предпосылка о гомоскедастичности остатков. В силу этого классический МНК в случае малых выборок даст смещенные оценки параметров.
Одним из возможных методов оценивания параметров модели (5.51) является метод инструментальных переменных. Суть метода состоит в том, что вместо лаговой зависимой переменной для которой нарушается предпосылка МНК, используется другая переменная z, называемая инструментальной. При этом инструментальная переменная должна обладать двумя свойствами:
— она должна быть тесно коррелирована с лаговой переменной 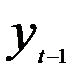 ;
;
— она не должна коррелировать с остатками 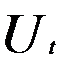 (случайными ошибками).
(случайными ошибками).
Иными словами, от модели авторегрессии (5.51) необходимо перейти к модели вида
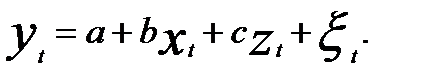 (5.52)
(5.52)
Результаты регрессии по модели (5.52), естественно, зависят от того, насколько удачно подобрана инструментальная переменная. В качестве инструментальной переменной можно, например, взять оценку 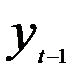 , т.е.
, т.е. 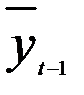 , полученную по регрессии
, полученную по регрессии 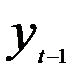 от
от 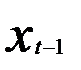 .
.
Поскольку в модели (5.52) предполагается наличие зависимости 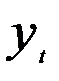 от
от 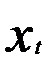 , то можно предположить, что также имеет место зависимость
, то можно предположить, что также имеет место зависимость 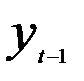 от
от 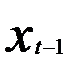 , т.е. найдем регрессию
, т.е. найдем регрессию
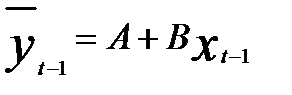 (5.53)
(5.53)
Используя для оценки параметров уравнения (5.53) обычный МНК, что возможно ввиду отсутствия в правой части модели лаговой зависимой переменной, найдем теоретические значения 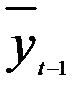 , которые и будут рассматриваться как значения инструментальной переменной z в модели (5.52). Далее вновь применяем МНК уже к модели (5.52), т.е. по существу оценка параметров модели авторегрессии (5.51) будет найдена исходя из модели вида
, которые и будут рассматриваться как значения инструментальной переменной z в модели (5.52). Далее вновь применяем МНК уже к модели (5.52), т.е. по существу оценка параметров модели авторегрессии (5.51) будет найдена исходя из модели вида
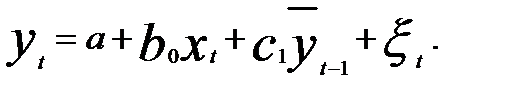 (5.54)
(5.54)
Если вместо оценки 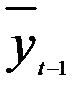 подставить выражение (5.53), то получим следующую модель:
подставить выражение (5.53), то получим следующую модель:
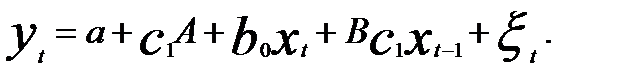 (5.55)
(5.55)
Она представляет собой модель с распределенным лагом, оценка параметров которой может быть дана МНК.
Таким образом, используя в качестве инструментальной переменной оценки 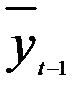 исходя из регрессии от
исходя из регрессии от 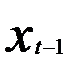 (5.53), модель авторегрессии (5.51 заменяют на модель с распределенным лагом (5.55).
(5.53), модель авторегрессии (5.51 заменяют на модель с распределенным лагом (5.55).
Вместе с тем следует отметить, что применение рассмотренной инструментальной переменной может привести при практической реализации модели (5.51) к появлению коллинеарности факторов. Объясняется это тем, что в модель (5.51) одновременно вводятся в качестве объясняющих переменных линейно связанные и высококоррелируемые между собой 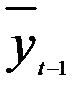 и
и 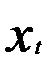 , ибо
, ибо 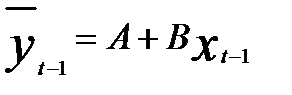 и
и 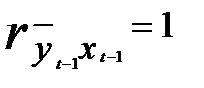 , а соответственно и
, а соответственно и 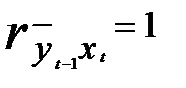 будет близок к единице. Однако если коллинеарность факторов не повлекла за собой неверные знаки у коэффициентов регрессии и не привела к большим стандартным ошибкам оценок, то применение инструментальной переменной можно считать возможным.
будет близок к единице. Однако если коллинеарность факторов не повлекла за собой неверные знаки у коэффициентов регрессии и не привела к большим стандартным ошибкам оценок, то применение инструментальной переменной можно считать возможным.
Пример 5.7
Применим метод инструментальных переменных к модели авторегрессии (5.51) по данным фирмы об импорте сырья (у — в т) товара и величине производства (х — в тыс. ед.) за январь — декабрь 2008—2009 гг.
| Годы | t | y(t) | x(t) | y(t-1) | x(t-1) |
Рассмотрим модель (5.51). Для оценивания параметров этой модели введем инструментальную переменную 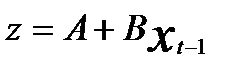 . Используя МНК, получим уравнение регрессии
. Используя МНК, получим уравнение регрессии
Уравнение регрессии значимо, как и его параметры. Далее вновь применяем МНК к модели (5.51), в которой вместо фактических значений у используется его предсказанное значение. Результаты оказались следующими:
Уравнение авторегрессии в целом значимо, значимыми являются и коэффициенты регрессии.
Если к модели (5.51) сразу же применить МНК, т.е. без введения инструментальной переменной, то результаты окажутся следующими:
Хотя коэффициент детерминации для модели, оцененной по обычному МНК, выше, чем для модели с инструментальной переменной, но коэффициент регрессии при 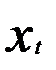 не только статистически не значим, но и имеет неверный знак, ибо увеличение объема продукции, на производство которой требуется ввоз сырья, ведет к росту величины импорта, что и показывает модель авторегрессии, оцененная с помощью метода инструментальных переменных.
не только статистически не значим, но и имеет неверный знак, ибо увеличение объема продукции, на производство которой требуется ввоз сырья, ведет к росту величины импорта, что и показывает модель авторегрессии, оцененная с помощью метода инструментальных переменных.
Дата добавления: 2016-03-22; просмотров: 2726;
