Алгебраические модели шифров.

Алгебраическая модель предложенная К. Шенноном.

Пусть X, K, Y – конечные множества открытых текстов, ключей и шифртекстов соответственно, |X| > 1, |K| > 1, |Y| > 1, E_k : X ® Y и D_k: E_k(X) ® X – правила зашифрования и расшифрования, отвечающие ключу k Î K, E = {E_k : k Î K}, и D = {D_k : k Î K}. Через E_k(X) мы обозначили множество E = {E_k(x) : x Î X}. Если ключ k Î K, представляется в виде пары k = (k_з, k_р), где k_з – ключ зашифрования, а k_р – ключ расшифрования (причем k_з ¹ k_р), то E_k понимается как E_kз, а D_k – как D_kр.

Определение: Алгебраической моделью шифра назовем совокупность

S_A = (X, K, Y, E, D)

введенных множеств, для которых выполняются условия

1) при любых x Î X и k Î K выполняется равенство D_k(E_k(x)) = x;

2) справедливо равенство .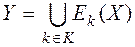

Условие 1) отвечает требованию однозначности расшифрования. Условие 2) означает, что любой элемент y Î Y может быть представлен в виде E_k(x) для подходящих элементов x Î X и k Î K. В общем случае E_k могут быть многозначными отображениями, но здесь мы ограничиваемся изучением лишь однозначных шифров, получивших наибольшее распространение.

Шифр называетсяэндоморфным, если Y = X. Для эндоморфного шифра правило зашифрования E_k осуществляет биективное отображение множества X на себя. В этом случае удобно рассматривать правила зашифрования как подстановки множества X, и опускать индекс в записи E_k, предполагая, что правила зашифрования пронумерованы ключами. По сути, вся информация об эндоморфном шифре содержится во множествах X и K.

Определение: Подстановочной моделью эндоморфного шифра назовем упрощенную совокупность S_П = (X, E)

Примеры.

1. Шифр простой замены в алфавите А:

Пусть 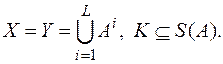, где S(A) – симметрическая группа подстановок множества А и L натуральное число. " k Î K, x = (x₁, .. x_l), y = (y₁, .. y_l): E_k(x) = (k(x₁), .. , k(x_l)),

D_k(y) = (k^-1(y₁), .. , k^-1(y_l)),где k^-1 – подстановка, обратная к k.

Подстановочной моделью данного эндоморфного шифра является совокупность (X, E), для которой e(x₁, .. x_l) = k(x₁), .. , k(x_l). Здесь x = x₁, .., x_l Î X, e Î E, а k – ключ, поставленный в соответствие подстановке e.

Шифр перестановки.

Пусть X = Y = A_L, K Í S_L, где S_L - симметрическая группа подстановок множества

{1, 2, .. , L}. " k Î K, x = (x₁, .. x_L), y = (y₁, .., y_L):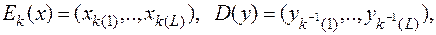

где k^-1 – подстановка, обратная к k.

Шифр RSA.

Пусть n = pq (q и p - простые), X = Y = Z_n – кольцо вычетов по модулю n.

K = {(n, p, q, a, b): a, b Î Z_n, n = pq, ab º 1(mod j(n))}, где j - функция Эйлера.

k = (k_з, k_р), где k_з = (n, b) и k_р = (n, p, q, a) – ключи. Правила зашифрования и расшифрования для x Î X и y Î Y определяются формулами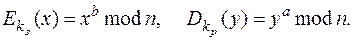

Уточним алгебраическую модель шифра, выбрав за основу модель, в которой открытыми и шифрованными текстами служат шифрвеличины и шифробозначения с которыми оперирует шифр. Назовем выбранную модель опорным шифром. Будем шифровать фрагменты открытого текста одним из априорно заданных правил зашифрования, составляющих опорный шифр. Назовем эти отображения простыми заменами. Простые замены будем выбирать при помощи вспомогательной последовательности, которую назовем ключевым потоком. Ключевой поток может определяться случайным образом или вычисляться детерминированно в зависимости от выбранного ключа шифра. Большинство шифров использует детерминированный ключевой поток.

Определение: Опорным шифра назовем совокупность

S = (U, K, V, E, D),

состоящую из: U и V - множеств шифрвеличин и шифробозначений с которыми оперирует шифр; K – множества ключей (номеров простых замен); E и D – множеств простых замен E_k : U ® V, k Î K, и обратных к ним отображений Dk : E_k(U) ® U.

Если шифр использует s простых замен, то примем в качестве множества ключей опорного шифра множество целых чисел K = {0, 1, …, s – 1}. Опорный шифр определяет способ зашифрования фрагментов открытого текста – шифрвеличин. Для работы с последовательностью шифрвеличин требуется степеньопорного шифра.

Определение: l-й степенью опорного шифра назовем совокупность множеств

S^l = (U ^l, K ^l, V ^l, E ^(l), D^(l)),

где U ^l, K ^l, V ^l - декартовы степени; множество E ^(l) состоит из отображений 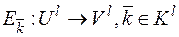, таких что для 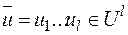и

;

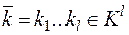
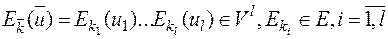множество D ^(l) состоит из отображений 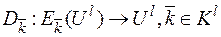, таких что для 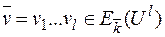и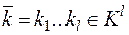

.

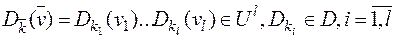Теперь рассмотрим построение ключевого потока, то есть последовательности k₁…k_l, k_j Î K, 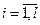, номеров простых замен, используемых для зашифрования открытого текста .

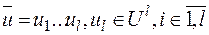Имеется два принципиально разных способа построения такой последовательности.

В первом случае она строится случайно. Устройство, вырабатывающее случайный ключевой поток называется случайным генератором ключевого потока. Формально его можно представить отображением y : N ® K*, (С* - множество слов конечной длины в алфавите С), ставящим в соответствие натуральному числу l последовательность из l испытаний некоторой случайной величины, принимающей значение из K с некоторыми ненулевыми вероятностями. Простейший случайный генератор – игровая рулетка.

Во втором случае шифр имеет некоторое, априорно заданное, конечное множество ключей K. Каждому ключу ĸ Î K и натуральному числу l Î N ставится в соответствие однозначно определенный ключевой поток k₁…k_l, k_i Î K, 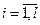. Этот поток вырабатывается детерминированным генератором ключевого потока.

Определение: пусть

y : K ´ N ® K*

- произвольное отображение, такое, что для любых ĸ Î K, l Î N, и некоторых k_i Î K, 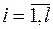, y(ĸ, l) = k₁ … k_l, причем {y(ĸ, l), ĸ Î K} = K. Назовем последовательность k₁ … k_l ключевым потоком, отвечающим ключу ĸ и числу l, а само отображение y - детерминированным генератором ключевого потока.

Если шифр использует случайный генератор, ключами шифра считают сами ключевые потоки. В таком случае, допуская вероятность зашифрования последовательности шифрвеличин любой конечной длины, мы получаем шифр с бесконечным множеством ключей. Если же шифр использует детерминированный генератор ключевого потока, множеством ключей является конечное множество K. Характер генератора ключевого потока делит все множество шифров на два класса.

Определение: Совокупность

S_Н = (S^l, l Î N; y),

- степеней опорного шифра, в которых для зашифрования последовательностей шифрвеличин u₁,…,u_l по правилу 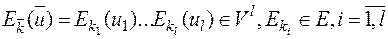ключевой поток строится с помощью случайного генератора y, назовем алгебраической моделью шифра с неограниченным ключом (или просто шифром с неограниченным ключом).

Определение: Совокупность

S_О = (S^l, l Î N; y),

- степеней опорного шифра, в которых для зашифрования последовательностей шифрвеличин u₁,…,u_l по правилу 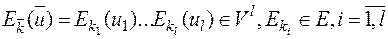ключевой поток строится с помощью детерминированного генератора y, назовем алгебраической моделью шифра с ограниченным ключом (или просто шифром с ограниченным ключом).

Криптографические свойства шифра с ограниченным ключом пределяются в первую очередь, свойствами его генератора ключевого потока. Например, если y(ĸ, l) = k’ … k’, для любого ĸ Î K и подходящего k’ Î K, то получаем «слабый» шифр простой замены. Если y(ĸ, l) = k₁ … k_p k₁ … k_p… представляет собой периодическую последовательность (в которой |{k₁ … k_p}| ³ 2), то получаем более стойкий шифр периодической замены. Например шифр Виженера.