Классификация шифров

Принятая в настоящее время классификация шифров приведена на рис.8. При этом условимся единицы открытого текста называть шифрвеличинами, а единицы шифрованного текста – шифробозначениями.

По характеру преобразований шифры делятся на два класса шифры замены и шифры перестановки, есть также композиционные шифры – последовательное применение двух предыдущих.

Шифры замены бывают симметричные (ключи зашифрования и расшифрования совпадают) и асимметричные (ключи различаются).

В зависимости от того, является ли правило зашифрования однозначной или многозначной функцией, шифры замены делят на шифры однозначной и многозначной замены.

В зависимости от размера шифрвеличин шифры замены делятся на поточные (n = 1) и блочные(n > 1).

При использовании для замены одинаковых шифробозначений для одинаковых шифрвеличин – одноалфавитный шифр замены, в противном случае – многоалфавитный. В отдельный подкласс многоалфавитных шифров выделяют шифры гаммирования, которые отличаются тем, что основной криптоалгоритм используется для выработки ключевой последовательности – гаммы, а достаточно простая функция шифрования используется для наложения ключевой последовательности на шифрвеличины.

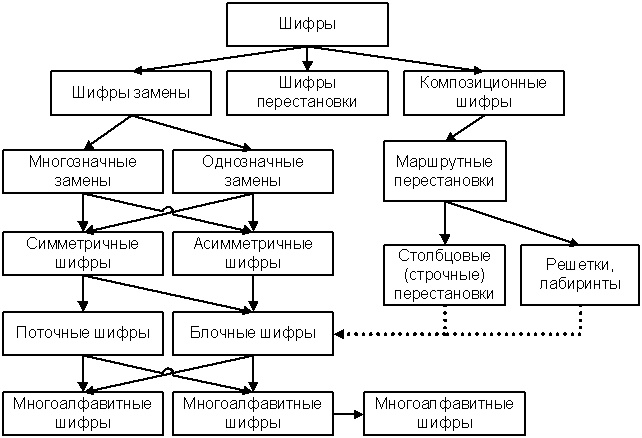
Рис.8. Классификация шифров.

Основой шифров перестановки служат маршрутные перестановки, которые делятся на столбцовые/строчные (вертикальные) перестановки, а также решетки, лабиринты и пр. В настоящее время шифры перестановки в чистом виде практически не не используются, но сами перестановки являются составляющей частью блочных криптоалгоритмов.

Композиционные шифры представляют собой сочетание в применении шифров замены и перестановки, а также блочных и поточных шифров. Четкой границы класса композиционных шифров не существует. Композиционным может стать любой блочный и поточный алгоритм, в зависимости от режима шифрования. Кроме того в настоящее время активно используются композиции симметричных и асимметричных шифров, такие как: RSA-OAEP, RSA-FDH, RSA-PSS, где симметричная составляющая используется для усиления слабых в реализации мест асимметричных алгоритмов.