Вероятностные модели шифров.

Введем теперь вероятностную модель шифра. Определим априорные распределения вероятностей P(X), P(K) на множествах X и K соответственно. Тем самым для любого x Î X определена вероятность p_X(x)ÎP(X) и для любого k Î K – вероятность p_K(k) Î P(K), причем выполняются равенства

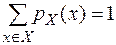и .

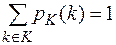В тех случаях, когда требуется знание распределений P(X) и P(K), мы будем пользоваться вероятностной моделью S_В, состоящей из пяти множеств, связанных условиями 1) и 2) предыдущего определения алгебраической модели шифра, и двух вероятностных распределений:

S_В=(X, K, Y, E, D, P(X), P(K)).

Распределение P(Y) индуцируется распределениями P(X) и P(K) согласно формуле полной вероятности:

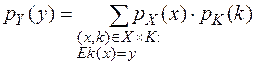
В большинстве случаев множества X и Y представляют собой объединения декартовых степеней A и B соответственно, так что для некоторых натуральных L и L₁

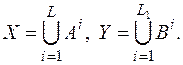
Множества A и B называют соответственно алфавитом открытого текста и алфавитом шифрованного текста. Другими словами, открытые и шифрованные тексты записываются привычным образом в виде последовательности букв.

Принята также формулировка вероятностной модели шифра в которой вместо включения в совокупность распределений случайных величин множества X, K Y, рассматриваются как случайные величины 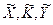, полагая при этом случайные величины 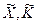независимыми.

Определение: вероятностной моделью шифра назовем совокупность

,

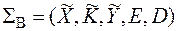введенных случайных величин, множество правил зашифрования и расшифрования. При этом выполняются требования, предъявляемые к алгебраической модели шифра. Для вероятностной модели шифра используется также обозначение .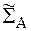

Пусть 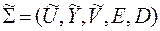- вероятностная модель опорного шифра. Введя априорные распределения вероятностей P(U^l) и P(K^l) на декартовых степенях множеств U и K, рассмотрим вероятностную модель l-го опорного шифра, рассматривая вместо U^l – множества всех l-грамм, множество U^(l), состоящее из тех l-грамм, для которых выполняется условие 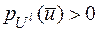, то есть всех незапрещенных l-грамм. Также вместо V^l будем рассматривать V^(l), полагая, что выполняется равенство .

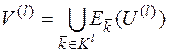Введем вероятностную модель шифра с неограниченным ключом.

Определение: Пусть для l Î N

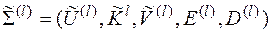
- совокупность, состоящая из случайных величин 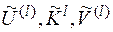, множеств правил зашифрования и расшифрования 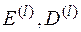, для которой выполняются условия

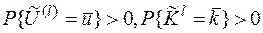
при любых 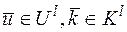. Тогда вероятностной моделью шифра с неограниченным ключом назовем семейство

,

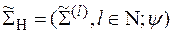где y - случайный генератор ключевого потока.

Аналогично вводится вероятностная модель шифра с ограниченным ключом, только вместо множества K^l всех ключевых потоков длины l, рассмотрим множество K^(l) возможных ключевых потоков длины l.

Определение: Пусть для l Î N

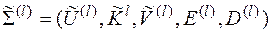
- совокупность, состоящая из случайных величин 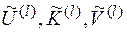, множеств правил зашифрования и расшифрования 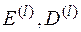, где распределение P(K^(l)) определяется формулой 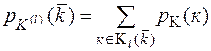и при любых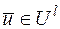

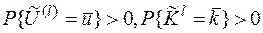
. Тогда вероятностной моделью шифра с ограниченным ключом назовем семейство

,

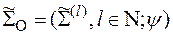где y - детерминированный генератор ключевого потока.