Алгоритмы и модели компоновки

В настоящее время при разработке современных электронно-вычислительных средств (ЭВС) основными элементами являются интегральные микросхемы (ИМС) - микроэлектронные изделия, выполняющие функции преобразования, обработки сигнала или накопления информации и имеющие высокую плотность упаковки электрически соединенных элементов и кристаллов, которые рассматриваются как единое целое. Под элементом ИМС понимается его часть, реализующая функцию произвольного электро-радио-элемента (ЭРЭ), не выделяемая как самостоятельное изделие. Компонент ИМС также реализует функцию ЭРЭ, но рассматривается как самостоятельное изделие. Сложность ИМС характеризуют числом содержащихся в них элементов и компонентов и называют степенью интеграции (СИ). Величину СИ определяют по формуле СИ = lgN, где N -число элементов и компонентов в ИМС.

При решении задач конструкторского проектирования радиоэлектронной и электронно-вычислительной аппаратуры с помощью САПР должно быть предусмотрено использование унифицированной конструкторско-технологической базы современной микроэлектроники. По этому они строятся по блочному принципу.

Основными элементами ЭВА являются монолитные интегральные БИС, СБИС, для которых значение СИ соответственно равны: 1000 (и более) и 10⁶ элементов и компонентов.

Конструкция ЭВА всегда содержит иерархию типовых элементов конструкций (ТЭК). Под ТЭК можно понимать конструктивно законченное изделие любой сложности.

Съемные ТЭК называют типовыми элементами замены (ТЭЗ).

Обычно говорят о конструировании на определенном ранге (уровне).

Например, к ТЭК первого (низшего) ранга относят транзисторы, резисторы, интегральные микросхемы (ИМС), модуль, микромодуль и т.д., т.е. конструктивно неделимый базовый элемент, на котором ведется конструирование.

На втором уровне элементы первого ранга, например ИМС, объединяются в схемные сочетания, образуя ТЭЗы (типовой элемент замены) или ячейки и т.д.

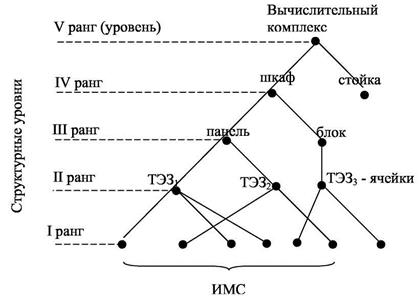Рисунок 2.6 – Структурные уровни РЭС.

Таким образом, ТЭК i-го ранга объединяются в ТЭК (i+1)-го ранга. Как правило, конструкторско-техническая база ЭВА состоит из пяти уровней (рангов) (рис. 2.6).

В общем случае при переходе от ранга i к рангу (i+1) приходится решать задачу компоновки, т.е. разбиения ТЭК уровня i на ТЭК уровня (i+1).

Исключение составляет компоновка элементов самого низкого ранга, которые составляются не из конструктивных элементов, а из функциональных базовых элементов.

Задачи компоновки на всех уровнях иерархии конструктивного оформления ЭВА тесно связаны между собой. Компоновка рассматривается как процесс принятия решения. В результате решения задачи компоновки типовые элементы конструкции (ТЭК) z'-го уровня, размещается в ТЭК (i+1)-го уровня. При этом учитывается выбранный критерий качества.

Преобразование функционального описания аппаратуры в соответствующее ему описание схемы электрической принципиальной может быть выполнено двумя способами: «снизу-вверх» и «сверху-вниз». На практике применяются оба способа и их различные комбинации. Например, можно функциональную схему (ФС_Х) устройства покрыть ТЭК второго ранга (ячейками), а затем уже схему каждой ячейки покрывать модулями.

Существует три варианта постановки задачи компоновки, в зависимости от принятых критериев:

- типизация - разбиение ФС_Х на части различных типов по критерию минимума числа разнотипных узлов (минимум номенклатуры узлов);

- покрытие - преобразование ФС_Х в принципиальную электрическую схему, т.е. в схему соединений ТЭК, номенклатура которых заранее известна;

- разрезание - разбиение ФС (или ПЭС) на части с минимизацией числа связи между этими частями и ограничением числа связей каждой части.

Исходными данными для решения задачи компоновки является коммутационная схема (КС). Для алгоритмизации и формального решения задачи производится переход от КС к графу одним из методов, описанных выше.

Классификация алгоритмов компоновки приведена на рис. 2.7:

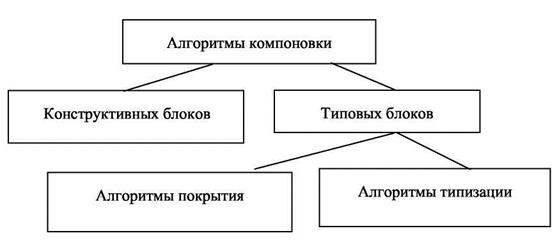
Рисунок 2.7 – Классификация алгоритмов компоновки.

Алгоритмы классифицируются по критериям, по ограничениям на формирование частей или по структуре вычислительной процедуры. С этой точки зрения их делят на последовательные, параллельно-последовательные и итерационные. В алгоритмах первого типа вводится последовательный процесс компоновки частей, на каждом шаге которого в очередную часть добавляется один из элементов математической модели, выбираемый по определенному приоритету. В параллельно-последовательных алгоритмах сначала выделяется некоторое исходное множество групп элементов, которое затем распределяется по частям с учетом критериев и ограничений на компоновку. Обычно эти алгоритмы используются при решении задач компоновки со специальными требованиями, например, минимизация числа разнотипных блоков. Итерационные алгоритмы служат для улучшения некоторого начального варианта компоновки в соответствии с принятым критерием.

При использовании итерационных алгоритмов сначала граф разбивается на определенное число частей произвольным образом, например с помощью последовательных алгоритмов. Затем по некоторым правилам производится перестановка вершин из одной части в другую с целью минимизации числа внешних ребер.

В алгоритмах разбиения, основанных на математических методах, в основном используются методы ветвей и границ, решение задачи о назначениях. Алгоритмы разбиения с применением методов ветвей и границ состоят из следующих этапов. Сначала определяется нижняя оценка разбиения графа на заданное число частей. Затем производится построение дерева решений и осуществляется поиск оптимального результата.

Задачу разбиения графа схемы на части можно свести к задаче о назначении.При этом ищется назначение кандидатов (вершин графа) на все части, дающие минимальные суммарные затраты. При этом каждая вершина может быть назначена только на одну часть и в каждой части должны содержаться различные вершины графа.

Алгоритмы компоновки типовых блоков сводятся к задачам покрытия итипизации.Под покрытиемпонимается представление функциональной схемы ЭВА типовыми конструктивными элементами, на которых она будет реализована, и связями между ними с выполнением заданных конструктивных ограничений. При покрытии выделяют задачи с несвязными элементами и функциональными ячейками. В первом случае решают задачи определения необходимого числа ячеек для покрытия коммутационной схемы с минимальной суммарной стоимостью (математическая модель 19 - 21). Во втором случае решают задачи покрытия коммутационной схемы заданным классом функциональных ячеек с минимизацией числа ячеек и суммарного числа межъячеечных связей (математическая модель 22 - 26).

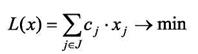(19)

при условиях (ограничениях)

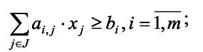(20)

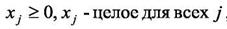(21)

где a_ij - количество элементов i-готипа, содержащееся в ячейке j-го типа;

x_j - количество ячеек j-го типа, используемых при покрытии элементов коммутационной схемы;

с_j - стоимость ячейки _j-го типа.

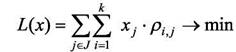(22)

при условиях (ограничениях):

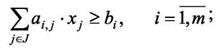(23)

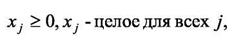
(24)

где: a_ij - количество элементов i-готипа, содержащиеся в ячейке j -го типа;

x_j - количество ячеек j-го типа, используемых при покрытии коммутационной схемы;

p_ij - количество внешних связей ячейки типа j при реализации ею элемента схемы i-готипа;

b_j - количество элементов i-готипа, содержащиеся в коммутационной схеме.

Типизация - это разбиение коммутационной схемы на части по критерию оптимальности - минимум номенклатуры частей разбиения или по критерию оптимальности - максимуму однотипности используемых ячеек. Сокращение номенклатуры ТЭК позволяет уменьшить затраты на дальнейшее проектирование.

Задача типизации - это компоновка «сверху вниз».

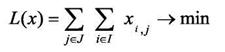(25)

при условиях (ограничениях):

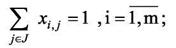(26)

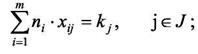(27)

x_ij = {0;1}, (28)

где x_ij - переменная проектирования; x_ij = 1, если ячейка типа j-гo реализует i-й элемент схемы; x_ij = 0, если ячейка j-гo типа не может реализовать i-й элемент схемы.

k_j - количество элементов, содержащиеся в ячейке j-гo типа;

n_i - количество элементов i-ro типа, содержащиеся в ячейке j-гo типа.

Ограничение (26) показывает, что каждый элемент коммутационной схемы может быть реализован только одной ячейкой соответствующего типа.

Ограничение (27) показывает, что число элементов схемы, реализуемых ячейкой j-гo типа не должно превышать числа элементов, содержащихся в ней.

Важной задачей в общей проблеме компоновки коммутационной схемы является покрытие. Как отмечалось выше, под покрытием схемы понимается представление функциональной схемы типовыми элементами конструкций, на которых она будет реализована, и связями между ними. Покрытие называют компоновкой «снизу в верх».

Решение задачи покрытия на первом уровне конструкторского проектирования дает возможность представить функциональную схему ЭВА или ее частей в виде принципиальной электрической схемы соединений элементов. Элементами могут быть резисторы конденсаторы, транзисторы, ИМС и т.д., т.е. ТЭК 1-го уровня. Поэтому при решении задачи покрытия можно рассматривать вопросы выбора класса элементов и минимизации числа типов элементов. Конечной целью покрытия является выбор оптимальной элементно-технической базы объекта проектирования.

Исходной информацией для этого этапа проектирования являются схема функциональная и набор ячеек Я= {Я₁,Я₂,...,Я_n}, параметры которых оказывают решающее влияние на результаты покрытия схемы.

Пусть задана схема, состоящая из элементовхи x₁, x₂,..., х_п, для каждого из которых известен тип t(x_i), t=1...l. Состав схемы по типам элементов описывается вектором M={m₁,m₂,...,m_t...,ml}, в котором m_t- число элементов типа t. Состав ячеек заданного набора Я описывается матрицей R ⁼ ||r_v,t||, v=(1...k), t={1...n}, где r_v,t - число элементов типа t в ячейке Я_v. Схема считается покрытой ячейками из набора Я, если каждый элемент схемы реализуется элементами, входящими в состав выбранных ячеек. Пусть известны стоимости c_v ячеек каждого типа. Требуется отыскать покрытие с минимальной стоимостью F:

F =∑c_v×|R_v|

Для формализации процесса покрытия схемы ячейками, различные наборы делятся на классы.

1. В состав ячеек входят логические элементы одного типа, не связанные между собой; входы и выходы элементов имеют отдельные выводы на ячейке.

2. Ячейки содержат разнотипные элементы, не связанные между собой; входы и выходы элементов имеют отдельные выводы на ячейке.

3. Состав ячеек аналогичен классу 1, однако часть элементов связана между собой.

4. Состав ячеек аналогичен классу 2, однако часть элементов связана между собой.

Рассмотрим задачу, относящуюся к классу 2. Математическая модель задачи покрытия для данного класса запишется:

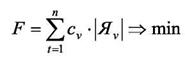(29)

при условиях:

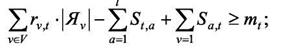(30)

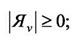(31)

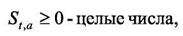(32)

где m_t - число элементов типа t, используемых в схеме;

S_t,a - количество элементов типа «t», которые могут быть заменены элементами типа «а»;

S_a,t - количество элементов типа «а», которые могут быть заменены элементами типа «t»;

|Я_v| - число ячеек типа Я_v, использованных при реализации схемы.

Задача (29-32) относится к задачам целочисленного программирования. Ее решение точными методами затруднено, поэтому применяют приближенную эвристическую процедуру решения поставленной задачи. На практике хорошо зарекомендовал себя алгоритм Селютина. Рассмотрим алгоритм Селютина компоновки ячеек с несвязными элементами. Пример такой ячейки «K155LA3» приведен на рисунке 2.8. В состав данной ячейки входят однотипные элементы, реализующие функцию «И-НЕ» на два входа.

Для общности примем, что набор ячеек относится к классу 2, т.е. в него входят ячейки с разнотипными элементами.

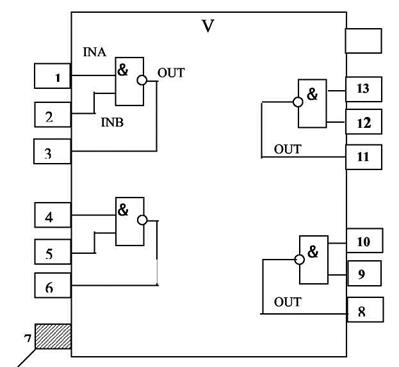Рисунок 2.8 – Структура ИМС К155Ла3.

При решении задачи будем считать, что каждый элемент схемы реализуется элементом того же типа в ячейках набора Я. В качестве дополнительного критерия оптимизации принимается число межъячеечных соединений. Решение задачи разбивается на два этапа:

1) определение необходимого числа ячеек с минимальной суммарной стоимостью;

2) минимизация числа связей между ячейками.

Пусть дана матрица R = ||r_ν,t ||, v ={1...k}, t={1...n}, и вектор числа элементов в схеме по типам М₀ = ||m_t ||.

Алгоритм решения задачи состоит в следующем.

1. Упорядочить ячейки набора {Я_у} по возрастанию их стоимости: Я₁,Я₂; Я_3,.., Яv (C₁≤C₂≤...≤С_k≤...≤C_v). Выбирается ячейка Я_к с наименьшим значением стоимости С_k. Задается начальное значение номера итерации i=0. По результатам структурного анализа покрываемой схемы определяется вектор М₀, элементы которого равны числу каждого типа элементов, использованных в схеме.

2. Определить «локально-минимальное» число ячеек Я_к для итерации i= i+1: A_k⁽ⁱ⁾ =min {m_t/r_k,t}, где r_k,t- количество элементов типа «t» в ячейке типа «k».

3. Вычислить вектор «непокрытых элементов» М_i:

М_i= М_i-1- A_k⁽ⁱ⁾R_k

4. Если M_i >0, перейти к п.2, если М_i= 0, перейти к п.5.

5. Подсчитать число ячеек каждого типа: |Я_ν|= ∑А_ν⁽ⁱ⁾ ,

где р -число выполненных при покрытии итераций; v = {1,2,3,...,k,...,v}.

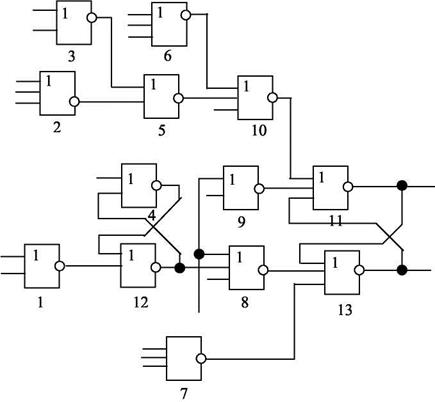
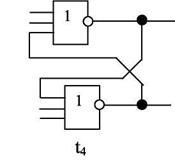
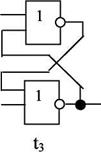
Пример.Дана логическая схема (рис.2.9) и типы используемых элементов (рис.2.10)

Рисунок 2.9 – Логическая схема устройства

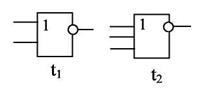Рисунок 2.10 – типы используемых компонентов.

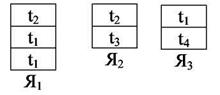Типовые элементы проектирования t₁, t₂, t₃, t₄входят в набор ячеек Я_1, Я₂, Я₃ (рис. 2.11):

Рисунок 2.11 – Типовые элементы.

Составим матрицу ||R_v|| описания состава данного набора ячеек:

Строки матрицы ||R_v|| соответствуют ячейкам заданного набора - Я_1, Я₂, Я₃. Столбцы - типовым элементам проектирования: t₁, t₂, t₃, t₄. Данные структурного анализа схемы приведены в таблице 1.

Таблица 1

В соответствии с исходными данными, математическая модель задачи покрытия запишется:

L = c₁x₁ + c₂x₂ + c₃x₃ →min (33)

при условиях:

2x₁+x₃≥5; (34)

x₁+x₂≥4; (35)

x₂≥2; (36)

x₃≥1; (37)

x_j≥0, x_j –целое число

где: x_j - количество ячеек j-го типа, выбранных для покрытия схемы.

Решение задачи покрытия по алгоритму Селютина.

1. По данным таблицы 1 запишем вектор М₀ = (5,4,1,1) .

2. Упорядочим ячейки заданного набора {Я_ν} по возрастанию их стоимости: Я₁;Я₂;Я₃ {С₁≤С₂≤С₃).

3. Выбираем ячейку Я₁, т.к. она имеет наименьшую стоимость.

Определяем «локально-минимальное» число А₁⁽¹⁾ использования ячейки Я₁. Ячейка Я₁ может реализовать элементы схемы типа t₁, t₂(см. матрицу R_v).

Для реализации элементов схемы типа t₁ требуется две ячейки Я₁→A_1,1=(5div2=2).

Для реализации элементов схемы типа t₂ требуется четыре ячейки Я₁→A_1,2=(4div1=4).

Для нашего примера А₁⁽¹⁾ =min { A_1,1, A_1,2); А₁⁽¹⁾ =2. Следовательно, |Я₁|=2 шт.

Переход к следующей итерации: i= i+1, i=0+1, i=1.

4. Вычисляем вектор «непокрытых элементов» M_i, где i – номер выполненной итерации (i=1).

M₁ = М₀ – А₁¹ ×r _1,1 ; получаем M₁= (1,2,1,1).

5. Так как вектор M₁ ≠ 0, то выполняем вторую итерацию (i =2) для ячейки Я₂. Все вычисления проводятся аналогично вычислениям на первой итерации, но с новыми значениями вектора M₁.

6. А₂²=min (A_2,2; A_2,3)= min (2; 1); А₂²=1; |Я₂|=1; M₂= (1,1,0,1).

Так как М₂>0, - выполняем 3-ю итерацию.

7. Третья итерация выполняется для ячейки Я₃.

А₃³=min (A_3,1; A_3,4)= min (1; 1);|Я3|=1;

Вычисляем М₃=(0,1,0,0).

Так как М₃>0, - выполняем 4-ю итерацию.

8. Вектор М₃ содержит только один ненулевой элемент - m₂. Следовательно в схеме остался только один нереализованный элемент типа t₂, который может быть реализован ячейками Я₁ и Я₂. Так как С₁<С₂ выбираем ячейку Я_1.

9. Вычисляем вектор М₄: М₄=(0,0,0,0).

Так как М₄ = 0, решение задачи заканчивается. Остается подсчитать суммарное количество ячеек каждого типа, вычисленное на каждой итерации. Для данного примера |Я₁| = 3, |Я₂|= 1, |Я₃| = 1.

Выше говорилось о том, что ячейка - это неделимый базовый элемент конструкции, поэтому при покрытии допускается некоторая избыточность элементов ячеек в виду их недоиспользования, например, одна из трех ячеек Я₁ имеет избыточность по элементам типа t₁.

Функциональную схему можно представить графом G=(X, U), где X -множество вершин, интерпретирующих логические элементы схемы, а множество ребер U - связи.

Пусть функциональную схему электронной радиоаппаратуры необходимо покрыть заданным комплексом интегральных микросхем (БИС).

Тогда каждый компонент БИС можно представить в виде подграфа G'. В результате получим некоторое множество подграфов, соответствующих ИМС заданного комплекса. Задача покрытия формулируется теперь как покрытие графа G подграфами из множества {G₁’, G₂’, ...,G’_p}. Один из возможных путей решения этой задачи следующий.

Каждой вершине графа G присвоить код S_i,p, где i - номер вершины; р - тип элемента логической схемы.

Каждому ребру графа ставится в соответствие значение функции веса g_i;k.

g_i;k=1, если ребро u_i, инцидентно однотипным вершинам;

g_i;k=0, в противном случае.

Внутри ИМС, как правило, объединяются однотипные компоненты. Из нескольких вариантов покрытия схемы выбирают тот, для которого:

Рассмотрим задачу типизации.

Типизация - это разбиение коммутационной схемы на части с минимизацией номенклатуры частей разбиения. Однотипными называются ТЭК, имеющие одинаковый состав элементов и одинаковую коммутационную схему. В этом случае задача типизации формулируется, как задача выделения в графе изоморфных подграфов (A.M. Бершадский): найти разбиение φ(G) из Ф графа G на множество групп изоморфных подграфов, удовлетворяющих следующим условиям:

1) любые два подграфа G_i,G_k, принадлежащие одной группе разбиения, должны быть изоморфны;

2) множества вершин любых двух подграфов не должны пересекаться;

3) число вершин любого подграфа разбиения не должно превышать заданное (конструктивное ограничение, связанное с числом элементов на типовом элементе конструкции);

4) суммарное число внешних ребер каждого подграфа не должно превышать заданное (конструктивное ограничение, связанное с числом элементов разъема или длиной параметра корпуса ТЭК).

Критерием оптимальности при типизации является минимальное число групп изоморфных подграфов, полученных в результате разбиения.

Для решения задачи типизации путем сведения ее к задаче выделения в графе изоморфных подграфов необходимо:

1) описать исходную коммутационную схему с помощью графовой модели;

2) решить для графа задачу выделения в нем изоморфных подграфов;

3) от полученных результатов решения задачи на графе необходимо перейти к результатам решения задачи типизации в коммутационной схеме.