Частотные характеристики.
Наиболее важная характеристика – избыточность открытого текста (подробно рассматривается в разделе надежности шифров).
Более простые:
· повторяемость букв, пар букв (биграмм), m-грамм;
· сочетаемость букв друг с другом (гласные-согласные и пр).
Такие характеристики устанавливаются на основе эмпирического анализа текстов достаточно большой длины.
Эксперимент по оценке вероятности появления в тексте фиксированных m-грамм (для небольших m).
Подсчет чисел вхождений каждой из nm возможных биграмм в достаточно длинных открытых текстах T = t1t2…tl, составленных из букв алфавита {a1, a2,…,an}. При этом просматриваются подряд идущие m-граммы текста:
t1t2…tm, t2t3…tm+1, … , t1- m+1tl-m+2…tl.
Если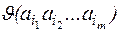 
- число появлений m-граммы 
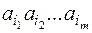в тексте T, а L – общее число подсчитанных m-грамм, то при достаточно больших L:
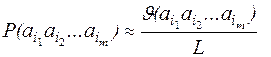
При анализе сочетаемости букв друг с другом используют понятие условной вероятности (зависимость появления буквы в тексте от предыдущих букв).
Для условных вероятностей выполняются неравенства:
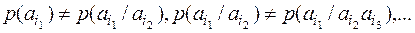
А. А. Марковым отмечена устойчивая закономерность чередования гласных и согласных. Зависимость появления букв текста вслед за несколькими предыдущими ощутима на глубину в 30 знаков, после чего практически отсутствует.
Вероятностная модель m-го приближения.
Пусть P(m)(A) – массив, состоящий из приближений для вероятностей p(b1b2…bm) появления m-грамм b1b2…bm в открытом тексте, m Î N, A = {a1,…,an}- алфавит открытого текста, bi ÎA,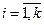 
. Тогда источник "открытого текста" генерирует последовательность c1,c2,…,ck,ck+1,… знаков алфавита A, в которой m-грамма c1c2…ck появляется с вероятностью
p(c1c2…cm)ÎP(m)(A).
Дата добавления: 2016-02-13; просмотров: 1013;