Временные и частотные характеристики звеньев второго порядка

ПФ звена второго порядка можно представить в нескольких формах записи:

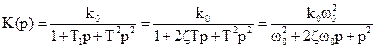, (5.34)

где z– коэффициент демпфирования. Возможно представление ПФ в виде

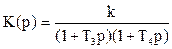. (5.35)

Наиболее общие формы – первая и вторая в (5.34). Третьей в (5.34) пользуются преимущественно для колебательных звеньев. Форма (5.35) удобна исключительно для апериодических звеньев.

Свойства апериодического и колебательного позиционных звена отличаются прежде всего разными значениями величин z.

Для апериодических звеньев второго порядка z ³ 1. Дляних характерна монотонная форма ПХ и плавная, без подъемов, АЧХ (ЛАЧХ), имеющая в области высоких частот крутизну спада 40 дБ/декаду (прил. 2).

ПХ такого звена определяется по формуле (прил. 1)

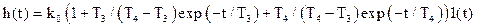, (5.36)

а ИХ – как

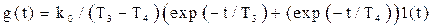. (5.37)

График ПХh (t) , приведенный на рис. 5.8, дает представление об определении параметров ПФ по экспериментальной характеристике.

(См. также рис. 5.9 и 5.10, график 4.)

Если в (5.35) – (5.37) Т₃ = Т₄ (z = 1 или Т₁ = 2Т₂ в (5.34)), то

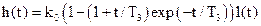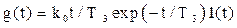, . (5.38)

При Т₄®0 звено вырождается в апериодическое звено первого порядка.

У колебательного звенаz < 1.

Если параметр демпфирования z лежит в пределах 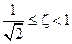, то на ПХ (рис. 5.9, график 3) появляется выброс (зона перерегулирования), хотя АЧХ (рис. 5.10) по существу не меняется.

По мере уменьшения z ярче проявляются резонансные свойства звена (рис. 5.10, графики 1 и 2), и соответственно увеличивается колебательность временных характеристик (число пересечений уровня h(¥) (рис. 5.9, графики 1 и 2) и g(¥).

Хотя при увеличении z уменьшается время запаздывания (Т_З1 – Т_З4 на рис. 5.9) и увеличивается максимальная скорость нарастания ПХ 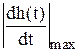, время регулирования из-за усиления колебательности процесса может даже увеличиться (на рис. 5.9 Т_Р1 > Т_Р2 > Т_Р3 < Т_Р4 ).

Число полных периодов колебаний N за время регулирования (N =1 на ПХ рис. 5.11, N =2 на ПХ рис. 5.9, гр. 1)

Временные характеристики колебательного звена описываются выражением

=

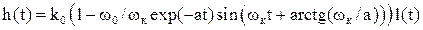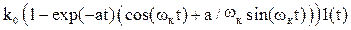= , (5.39)

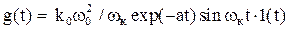. (5.40)

В (5.39)–(5.40) 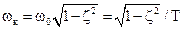– собственная частота колебаний звена; 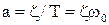– коэффициент затухания; также a и w_кявляются соответственно действительной и мнимой частями корней характеристического уравнения звена ( 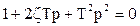) [17, 18]:

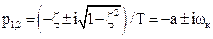. (5.41)

Графики звена второго порядка с колебательной ПХ изображены на рис. 5.9 и 5.11.

График на рис. 5.11 иллюстрирует, как по экспериментальной ПХ реального звена можно найти параметры соответствующего колебательного звена.

С погрешностью менее 25% при γ ³ 8 %, кроме формул (5.30) и других, приведенных ранее, можно оценить некоторые параметры ПХ с помощью эмпирических формул [13, 17, 20]:

Т_у2 = Т_н – Т_у; Т_у1 = Т₀₉ – Т_зап; 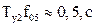; 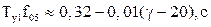. (5.42)

Если параметр демпфирования z лежит в пределах 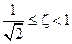, то АЧХ по существу не меняется (рис. 5.10) по сравнению с апериодическим звеном (z ³ 1), хотя на ПХ (рис. 5.9, график 3) появляется выброс.

Только в случае 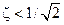наблюдается заметный подъем АЧХ в некотором диапазоне частот, при этом показатель колебательности М и «резонансный горб» увеличиваются с уменьшением z. Обычно резонансная частота w₀ несколько ниже w_к , но приближается к ней с ростом z (рис. 5.10).

На рис. 5.12 приведены примеры нормированных АЧХ звеньев второго порядка: апериодического (график 1) и колебательного (график 2).

Пример 5.2. Проанализируем показатели качества и взаимосвязь временных и частотных характеристик на примере апериодического и колебательного звеньев.

За основу возьмем частотные зависимости (АЧХ), показанные на рис. 5.10. Частота w на этих графиках изменяется от 0 до 22 рад/с.

Для графика 1 получаем (z₁=0,3) : М = 1,93, w₀ = 9,3 рад/с, w_п = 5,9 рад/с, w_ср = 13,1 рад/с, w₀₇ = 14,7 рад/с, w₀₅ = 16,8 рад/с.

Для графика 2 находим (z₂=0,5) : М = 1,15, w₀ = 6,9 рад/с, w_п = 11,7 рад/с, w_ср = 10,0 рад/с, w₀₇ = 12,7 рад/с, w₀₅ = 15,3 рад/с.

Для графика 3 – (z₃=0,8) : М = 1, w_п = w₀₇ = 8,7 рад/с, w₀₅ = 12,7 рад/с.

Для графика 4 – (z₄=1,1) : М = 1, w_п = w₀₇ = 5,6 рад/с, w₀₅ = 15,3, рад/с.

С помощью формулы (5.29) оценим Т_Р :

Т_Р1 = 0,5…2,0 с, Т_Р2 = 0,3…1,1 с, Т_Р3 = 0,36…1,4 с, Т_Р4 = 0,56…2,2 с.

Оценим с помощью формулы (5.30) Т_Р и γ при М > 1:

Т_Р1 = 1,4 с, γ₁ = 48%, Т_Р2 = 0,57 с, γ₂ = 9%.

Зная w₀, найдем период Т_к и частоту колебаний w_к ПХ с помощью (5.40):

w_1к = 8,9 рад/с, w_2к = 5,7 рад/с, Т_1к = 0,7 с, Т_2к = 1,1 с.

Сравним полученные результаты с прямыми оценками показателей качества, которые определяются из графиков ПХ, показанных на рис. 5.9 (t изменяется от 0 до 1,2 с): Т_Р1 = 1,07 с, Т_Р2 = 0,53 с, Т_Р3 = 0,34 с, Т_Р4 = 0,47 с; γ₁ = 42%, γ₂ = 15%, γ₃ = 2%, γ₄ = 0%, Т_1к = 0,7 с, Т_2к > 1 с. К(w=0) = h(¥) = k₀. К(w®¥) = h(0)=0.

Оценим с помощью формулы (5.42) временные параметры (рис. 5.11) ПХ при М > 1: для графика 1 (z=0,3) получаем Т_у1 = 0,02 с, Т_у2 = 0,19 с; а для графика 2 (z=0,5) – Т_у1 = 0,09 с, Т_у2 = 0,21 с (эти параметры позволяют оценить скорость нарастания ПХ на начальном участке).

Сравним полученные результаты с оценками показателей качества, которые можно определить из графиков ПХ, показанных на рис. 5.9.

Для графика 1 (z=0,3) получаем Т₀₉ – Т_зап = Т_у1 = 0,05 с, Т_н – Т_у = Т_у2 = 0,15 с; а для графика 2 (z=0,5) – Т₀₉ – Т_зап = Т_у1 = 0,08 с, Т_н – Т_у = Т_у2 = 0,21 с.

Таким образом, временные оценки, полученные косвенно из частотных характеристик, качественно совпадают с прямыми оценками, полученными из ПХ.

Пример 5.3. Найдем показатели качества и оценим взаимосвязь временных и частотных оценок для ФАПЧ из примера 4.2. Рассмотрим только вариант с наибольшим запасом устойчивости (Т2 = 4,7 мс, k₀ = 200 (46 дБ)).

Графики ЛАЧХ и ЛФЧХ разомкнутой системы были построены на рис. 4.12 (график 1). Запас устойчивости по усилению составил >40 дБ, а запас по фазе ≈15°, ωср1 = 45 рад/с, ωкр1 = 400 рад/с. Система астатическая первого порядка.

Характеристика P(w) показана на рис. 5.7 (график 3).

Построим АЧХ замкнутой системы (рис. 5.13), для этого сделаем замену р®iw в формуле (4.10) и выделим модуль.

Построим ПХ замкнутой системы (рис. 5.14), для этого разделим формулу (4.10) на р и выполним обратное преобразование Лапласа.

Из графика АЧХ находим частотные оценки : М = 4,8, w₀ = 44,2 рад/с, w_п = 9,5 рад/с, w_ср = 62,5 рад/с, w₀₇ = 68,8 рад/с, w₀₅ = 76,8 рад/с, z=0,11.

Из графика ПХ определяем временные параметры: Т_Р = 0,64 с, h_max1=1,72, γ = 72%, N=4, h_max2=1,35, u=2, а=4,7 1/с; Т_м1=70 мс, Т_к = 0,14 с (w_к = 44,4 рад/с), Т_зап = 25 мс, Т_н = 38 мс. Подтвердились выводы о колебательности ПХ.

Рассчитаем некоторые временные параметры, используя косвенные оценки.

Зная М, найдем с помощью формулы (5.32) запас по фазе: φ_з = 13°.

С помощью формулы (5.29) оценим Т_Р: Т_Р = 0,3…1,3 с.

Оценим с помощью формулы (5.30) Т_Р и γ: Т_Р = 1 с, γ = 130%.

Оценим с помощью формулы (5.42) временные параметры нарастания ПХ: Т_у1 = 0 с, Т_у2 = 40 мс. Сравним их с временными параметрами, полученными из анализа ПХ на рис. 5.14: Т₀₉ – Т_зап = Т_у1 = 35–25=10 мс, Т_н – Т_у = Т_у2 = 38–4=34 мс.

Пример 5.4. Найдем показатели качества и оценим взаимосвязь временных и частотных оценок для РАС из примера 4.5. Графики ЛАЧХ и ЛФЧХ были построены на рис. 4.14. Запас устойчивости по усилению составил 40 дБ, а запас по фазе ≈60°, ωср = 100 рад/с, ωкр = 1000 рад/с. Система статическая.

График P(w) показан на рис. 5.15, его поведение напоминает график 2 на рис. 5.7. Согласно косвенным оценкам ПХ должна быть малоколебательной.

Построим АЧХ замкнутой системы (рис. 5.16), для этого получим H(р):

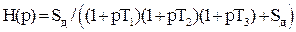, (5.43)

а затем H(iw) и выделим модуль. H(0)= h(¥) =Sд/(Sд+1)=10/11.

Построим ПХ замкнутой системы (рис. 5.17), для этого разделим в полученной формуле H(р) на р и выполним обратное преобразование Лапласа.

Из графика АЧХ находим частотные оценки : М = 1,13, w₀ = 72 рад/с, w_п = 122 рад/с, w_ср = 84 рад/с, w₀₇ = 132 рад/с, w₀₅ = 158 рад/с.

Из графика ПХ определяем временные параметры: Т_Р = 51 мс, h_max1=1,03, γ = 13%, N=1, z=0,52, u=1,02, а=54,5 1/с; Т_м1=35 мс, Т_к = 70 мс (w_к = 89,8 рад/с), Т_зап = 13 мс, Т_н = 24 мс. Подтвердились выводы о малоколебательности ПХ.

Рассчитаем некоторые временные параметры, используя косвенные оценки.

Зная М, найдем с помощью формулы (5.32) запас по фазе: φ_з = 62°.

С помощью формулы (5.29) оценим Т_Р: Т_Р = 0,3…1,0 с.

Оценим с помощью формулы (5.30) Т_Р и γ: Т_Р = 48 мс, γ = 3%.

Оценим с помощью формулы (5.42) временные параметры нарастания ПХ: Т_у1 = 9 мс, Т_у2 = 23 мс. Сравним их с временными параметрами, полученными из анализа ПХ на рис. 5.14: Т₀₉ – Т_зап = Т_у1 = 21–13=8 мс, Т_н – Т_у = Т_у2 = 24–2=22 мс.

Найдем корни характеристического полинома (знаменателя формулы (5.43)) с помощью программы MathCad. При заданных условиях получаем такие корни: р₁=–1×10⁴; р_2,3=–54,5±i89,6.

Таким образом, подтвердились сделанные ранее выводы о характере процессов РАС, рассмотренных в примерах 5.3 и 5.4, и о взаимосвязи временных и частотных параметров.