Косвенные оценки качества переходного процесса

К косвенным показателям качества переходного процесса относят частотные, корневые и интегральные оценки [1, 10].

Чаще всего используются частотные показатели качества, которые определяют по АХЧ замкнутой системы (K_λy(ω) и т. д.), ЛФЧХ и ЛАЧХ разомкнутой системы и по вещественной части P(ω) ЧПФ замкнутой системы (2.39).

Частотная характеристика астатической системы представлена на рис. 5.6.

К частотным показателям качества относятся.

1. Полоса пропускания ω_п – полоса частот, в которой АЧХ превышает единицу. У астатической РАС ω_п= ω_ср. Если АЧХ во всем диапазоне частот меньше единицы, то ω_п отсчитывается по уровню 0,71. В этом случае ω_п= ω₀₇, где ω₀₇ – полоса пропускания РАС по уровню 0,71 (половинной мощности).

2. ω₀ – резонансная частота, которая отсчитывается по максимуму АЧХ замкнутой системы и определяет частоту колебаний ω_к в переходном режиме. При такой АЧХ полосу пропускания ω_п правильнее оценивать по уровню 0,71 (–3 дБ) от максимального значения АЧХ.

3. Частота среза АЧХ (ЛАЧХ) разомкнутой системы ω_ср.

4. Показатель колебательности М – отношение максимального значения АЧХ K_λy(ω_р) к значению на постоянном токе K_λy(0):

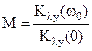. (5.28)

Обычно желательно иметь М ≤ 2.

При М > 1,5 – ПХ имеет колебательный характер (N³2),

если 1,1< М <1,5, то ПХ имеет малоколебательный характер (N<2),

при М ≤ 1 характер ПХ будет апериодическим.

Рассмотрим связь некоторых частотных показателей качества с основными показателями качества быстродействия РАС.

Время регулирования Т_р можно оценить по формуле

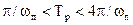. (5.29)

Также при М > 1 можно использовать эмпирические соотношения [13, 17] :

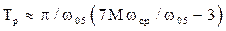, с; , (5.30)

где ω₀₅ – циклическая частота, на которой АЧХ имеет значение 0,5K_λy(0).

Погрешности данных эмпирических формул не превышают 25%.

Существует связь между показателем колебательности М и запасом устойчивости по фазе φ_з. На частоте ω_п H(ω_п)=1, тогда из формулы (2.37) получаем 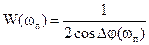. В диапазоне частот ω_ср и ω_п ЛАЧХ разомкнутой системы имеет наклон –20дБ/дек, поэтому ФЧХ в этом диапазоне изменяется мало, что после упрощения ∆φ(ω_п) ≈ ∆φ(ω_ср) = φ_з в результате дает

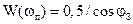. (5.31)

Полоса пропускания ω_п и частота среза ω_ср связаны соотношением:

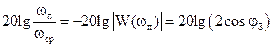, откуда следует .

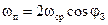Если исследовать (2.37) на максимум [4], и подставить в результат (5.31) и полученные формулы, получим [1, 4]:

. (5.32)

Анализ формулы (5.32) подтверждает сделанные ранее выводы о характере ПХ при определенных значениях М и φ_з.

По вещественной части P(ω) ЧПФ замкнутой системы (2.39) можно также судить о характере ПХ РАС, на основании анализа формул (2.40) [10, 20].

, (5.33)

где P_max(ω) – наибольшее значение P(ω).

Если P(ω) монотонно убывающая функция (P(ω)~1/ω), то ПХ будет иметь апериодический характер (рис. 5.7 график 1).

Если функция P(ω) имеет неубывающий (постоянный) участок АЧХ, то ПХ будет иметь малоколебательный характер (γ<18%) (рис. 5.7 график 2).

Если функция P(ω) имеет возрастающий участок («резонансный горб») АЧХ, то ПХ будет иметь колебательный характер (γ>18%). (рис. 5.7 график 3).

сужение полосы пропускания приводит к усилению колебательности переходного процесса,

у устойчивых систем с достаточным запасом устойчивости по фазе в области частоты среза ЛАЧХ как правило имеет наклон не более –20дБ/дек.