Желаемая передаточная функция разомкнутой системы

Предполагаем, что требования к ошибкам системы заданы:

(6.3.) где - ошибки системы по положению, скорости и ускорению.

На первом этапе определяется желаемая передаточная функция разомкнутой системы, которая позволяет удовлетворять заданным требованиям к проектируемой системе:

(6.4.)

(6.5.)

При синтезе систем с астатизмом I порядка:

(6.6.)

(6.7.)

При проектировании систем с астатизмом II порядка желаемая передаточная функция имеет вид:

(6.8.)

Задача синтеза сводится к определению по заданным показателям качества параметров желаемой передаточной функции К, Т₁, Т₂ и Т₃. Звенья с постоянными времени Тi в такой функции учитывают влияние на синтез РА центров с малыми постоянными времени (2Δ приемника РЛС в системе автоматического сопровождения цели и т.п.).

Проанализируем вначале типичные ЛАЧХ, соответствующие передаточным функциям (6.6.), (6.7.)

Найдем параметры желаемой передаточной функции системы (6.6.). По заданному значению колебательности системы и формуле (М=1/sinΔφ) вычисляют запас устойчивости по фазе: 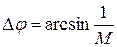(6.9.)

Так как полоса пропускания и частота среза связаны соотношением: (4.32.), то можно при требуемом значении полосы пропускания получить выражение для ω_ср: ω_ср = ωn/2cosΔφ (6.10.).

По допустимым значениям ошибок по скорости и ускорению находим коэффициенты ошибок:

С₀=0; (6.11.)

где 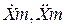- максимальное значение первой и второй производных от управляющего воздействия.

Коэффициент ошибки по скорости определяет коэффициент усиления в системе РА: К=1/С₁ (6.12.)

Для нахождения постоянных времени Т₁ и Т₂ установим связь сопряженных частот ω₁=1/Т₁ и ω₂=1/Т₂ с коэффициентом усиления и частотой среза. (6.13.).

Наклон характеристики между частотами ω₁ и ω₂ равен 40дб/дек, поэтому:

(6.14.).

Согласно (6.13.) и (6.14.) имеем К/ω_ср= ω₂/ω₁=Т₁/Т₂ (6.15.)

Постоянные времени Т₁ и Т₂ можно получить и из выражения для коэффициента ошибки по ускорению:

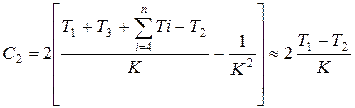(6.16.)

Упрощения в (6.16.) не приводят к нарушению требований по точности работы проектируемой системы. Из выражений (6.15.) и (6.16.) находим, что

(6.17.)

Постоянная времени Т₃ функции (6.6.) определяется из условия обеспечения в системе запаса устойчивости (6.9.):

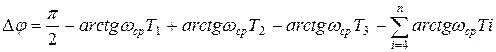(6.18.).

При высоких требованиях к точности не всегда можно удовлетворить заданные условия, используя функцию (6.6.), поэтому приходится применять более сложную передаточную функцию (6.7.). Коэффициент усиления в этом случае вычисляют по формуле (6.12.), а постоянные времени Т₁ и Т₂ в соответствии с выражениями:

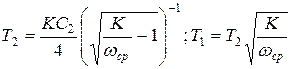(6.19.)

Постоянную времени Т₃ рассчитывают по формуле:

(6.20.)

Аналогичным образом определяются параметры желаемых передаточных функций статистических систем РА (6.4.) и (6.5.) и систем с астатизмом второго порядка (6.8.).