Понятие эквивалентной шумовой полосы пропускания системы
Определение дисперсии и СКО рассмотренным выше методом при больших порядках интеграла (6.14) оказывается затруднительным. Поэтому был разработан графоаналитический метод [10], в основу которого положен геометрический смысл интеграла: значение интеграла равно площади, которая находится под графиком подынтегральной функции.
Для вычисления дисперсии по формуле (6.13) или (6.11)–(6.13) строят график подынтегральной функции 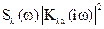 +
+ 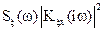 (в докомпьютерные времена эти построения выполняли по точкам, взятым на различных частотах ωj [10]) и вычисляют площадь под ним (в докомпьютерные времена эти вычисления осуществляли с помощью аппроксимации графика и площади под ним прямоугольниками и трапециями [10] и т. п.).
(в докомпьютерные времена эти построения выполняли по точкам, взятым на различных частотах ωj [10]) и вычисляют площадь под ним (в докомпьютерные времена эти вычисления осуществляли с помощью аппроксимации графика и площади под ним прямоугольниками и трапециями [10] и т. п.).
С учетом четности подынтегральной функции достаточно построить график только для положительных частот (формула (6.9)).
 . (6.24)
. (6.24)
В настоящее время вычисления проще всего проводятся с помощью численного интегрирования в специальных математических программах.
Пример 6.3.Найдем дисперсию для РАС и возмущения, рассмотренных в примере 6.1. После подстановки ЧПФ (6.17) и S(ω) формула (6.18) имеет вид:
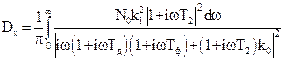 . (6.25)
. (6.25)
 После подстановки численных значений строим график подынтегральной функции (рис. 6.1) и вычисляем площадь (это удобно сделать с помощью разбиения на 1 прямоугольник и 3 треугольника, как показано на рис. 6.1). После вычисления площадей получаем Sэкв ≈ 3,4×10–3, подставляя в (6.24) вычисляем Dx ≈ 3,4×10–3/p ≈ 1,08×10–3.
После подстановки численных значений строим график подынтегральной функции (рис. 6.1) и вычисляем площадь (это удобно сделать с помощью разбиения на 1 прямоугольник и 3 треугольника, как показано на рис. 6.1). После вычисления площадей получаем Sэкв ≈ 3,4×10–3, подставляя в (6.24) вычисляем Dx ≈ 3,4×10–3/p ≈ 1,08×10–3.
С помощью численного интегрирования в MathCad, можно вычислить площадь и дисперсию (6.20) напрямую: Sэкв = 3,32×10–3, тогда Dx = 3,32×10–3/p = 1,06×10–3, что совпадает с полученным ранее значением.
Пример 6.4.Найдем дисперсию для РАС и возмущения, рассмотренных в примере 6.2. После подстановки численных значений в ЧПФ (формула (6.21)) и S(ω), а затем в формулу (6.18) строим график подынтегральной функции (рис. 6.2) и вычисляем площадь (это удобно сделать с помощью разбиения на 1 трапецию и 1 треугольник.
После вычислений получаем
Sэкв ≈ 1,3×10–3, Dx ≈ 1,3/p ≈ 4,1×10–4.
При численном интегрировании в MathCad дисперсия Dx = 4,2×10–4.
Если на РАС действует широкополосная помеха с равномерным спектром, ее можно считать белым шумом. В этом случае вводят понятие эквивалентной шумовой полосы (рис. 6.2), под которой понимается величина, равная полосе пропускания эквивалентной РАС с прямоугольной АЧХ, с одинаковой с исходной системой ЧПФ на нулевой частоте (рис. 6.2) и одинаковой дисперсией выходного процесса при действии на входах этих систем белого шума.
Из приведенного определения и выражения (6.13) вытекает (будем рассматривать только положительные частоты f или ω) формула:
 . (6.26)
. (6.26)
Для графика на рис. 6.1 эквивалентная шумовая полоса ωэф образует прямоугольник по уровню ≈1×10–5 и до частоты ωэкв ≈ 330 рад/с.
Для графика на рис. 6.2 эквивалентная шумовая полоса ωэф образует прямоугольник по уровню ≈9×10–6 и до частоты ωэкв ≈ 159 рад/с.
Если S(ω) случайного процесса отличается от константы, этот процесс можно свести к белому шуму, добавив в схему устройство, называемое формирующим фильтром [1, 4], на выходе которого будет процесс с той же S(ω).
В табл. 6.1 приведены некоторые формулы для определения fэф по ПФ W(p).
Табл. 6.1
| W(p) | fэф |
| k/p или k/p(1+pT) | 0,5k |
| k/(1+pT) | 0,5k2/(T(1+k)) |
| k/(p(1+pT1)(1+pT2)) | 0,5k(T1+T2)/(T1+T2 – kT1T2) |
| k(1+pT2)/(p(1+pT1)(1+pT3)) | 0,5k(T1+kT22+T3)/(T1+T3+k(T1T2+T2T3 –T1T3)) |
| k(1+pT2)/(p(1+pT1)) | 0,5k(T1+kT22)/(T1+kT1T2)=0,5k(1+kT2T2/T1)/(1+kT2) |
| k(1+pT)/p2 | 0,5(1+kT2)/T |
Пример 6.5.Найдем дисперсию при возмущении ξ(t) = N0 для РАС, схема которой показана на рис. 5.1, при ПФ звеньев K1=Sд – безынерционный дискриминатор, K2=k0(1+pT2)/(p+p2T1) – интегратор вместе с пропорционально-интегрирующим фильтром (ПИФ).
Для ПФ ошибки по возмущению из (2.30) после подстановки имеем:
 . (6.27)
. (6.27)
После замены переменных р® iω и подстановки в (6.14) получим:
 ,
,  . (6.28)
. (6.28)
Подставляя эти значения в (6.16) найдем дисперсию:
 , (6.29)
, (6.29)
где a=Т2/Т1 – отношение постоянных времени ПИФа.
С помощью понятия эквивалентной шумовой полосы можно было определить дисперсию по-другому. Для этого необходимо перенести пересчитать воздействие ко входу дискриминатора (ξд(t) = N0/Sд2) и воспользоваться формулой (6.26) и табл. 6.1 при W(p)=K1K2=k0Sд(1+pT2)/(p+p2T1):
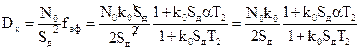 . (6.30)
. (6.30)
Рассмотрим некоторые соотношения параметров РАС и проанализируем их влияние на характеристики системы.
При Т2=0, получается то же соотношение для fэф, что и для фильтра системы, состоящему из одного интегратора (для Dx значение Т1 не имеет значения!):
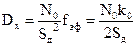 . (6.31)
. (6.31)
Из формулы (6.31) видно, что РАС с одним интегратором в контуре управления по фильтрации шумов эквивалентна инерционному звену с постоянной времени Т1 = 1/k0Sд , на вход которого подан шум с S(ω)=N0/Sд2.
Если на входе такого фильтра действует шум с S(ω)=N0, то 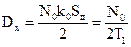 .
.
В случае применения в системе ПИФ существует оптимальное значение параметров Т2 и a, при которых дисперсия ошибки минимальна.
Пример 6.6.Определим дисперсию ошибки слежения в установившемся режиме в РАС из примера 6.5 при Т2=Т1=0, т. е. 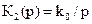 . Считаем, что ξ(t)=0, а воздействие λ(t) является стационарным случайным процессом со спектральной плотностью
. Считаем, что ξ(t)=0, а воздействие λ(t) является стационарным случайным процессом со спектральной плотностью 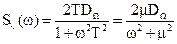 и дисперсией DW. Такой процесс характерен для входного сигнала РАС при слежении радиолокационной системы за движущимся с угловой скоростью W объектом. m=1/Т – среднее число перемен скорости за период времени, равный 1 секунде (или Т=1/m – среднее значение интервала времени, в течение которого W сохраняет постоянное значение) [1–5].
и дисперсией DW. Такой процесс характерен для входного сигнала РАС при слежении радиолокационной системы за движущимся с угловой скоростью W объектом. m=1/Т – среднее число перемен скорости за период времени, равный 1 секунде (или Т=1/m – среднее значение интервала времени, в течение которого W сохраняет постоянное значение) [1–5].
 . (6.32)
. (6.32)
С учетом (6.32) Для приведения интеграла к виду (6.14) преобразуем следующим образом:
 . (6.33)
. (6.33)
Из сравнения (6.33) с (6.14) вытекает, что в данной задаче n=2; b1=–2μDW, b0=0; a2=1, a1=μ+k0Sд, a0=μk0Sд. Подставляя эти значения в (6.16) получаем:
 . (6.34)
. (6.34)
В данном случае вычисление дисперсии через fэф затруднительно из-за сложных преобразований S(ω) и отсутствия соответствующей W(p) в табл. 6.1.
Таким образом, дисперсия ошибки данной РАС зависит от дисперсии воздействия DW, ширины спектра этого воздействия, характеризующейся параметром μ=1/Т, и коэффициента передачи по контуру управления k0Sд.
Дата добавления: 2016-02-20; просмотров: 3555;
