Энтропия и избыточность языка.
Свойства текстов изучаются методами теории информации, разработанной К. Шенноном. Ключевое понятие – энтропия, определяемая функцией от вероятностного определения и характеризующая количество неопределенности или информации в случайном эксперименте. Неопределенность и информацияизмеряются одной и той же мерой. Применительно к независимым испытаниям случайной величины x с распределением вероятностей
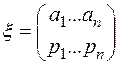
энтропия H(x) определяется формулой

Единицей количества информации считается 1 бит. При pi = 1/n при всех 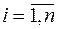 , то
, то
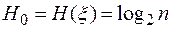 .
.
Мерой среднего количества информации, приходящейся на одну букву открытого текста языка L (рассматриваемого как источник случайных текстов), служит величина HL, называемая энтропией языка L. вычисляется последовательными приближениями позначных моделей текста: H1, H2, … Hr.
Для каждого языка значение HL стремится к определенному пределу (после r = 30 предел уже устанавливается):
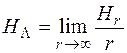 .
.
при этом формула
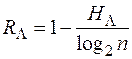
определяет избыточность языка RL. Разговорные языки имеют весьма большую избыточность. Избыточность текста в 75% означает, что при оптимальном кодировании текста (например использование кодов Хаффмена, Фано или других) его можно сжать до четверти без потери информации.
Энтропию можно определить и по другому. Для n-буквенного алфавита число текстов длины L, удовлетворяющих статистическим ограничениям, равно (при достаточно больших L) не 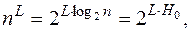 как это было бы, если бы мы имели право брать любые наборы из L букв, а всего лишь
как это было бы, если бы мы имели право брать любые наборы из L букв, а всего лишь
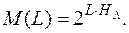
По сути это приближенное число осмысленных текстов длины L для данного языка L. Исходя из этого можно определить энтропию языка формулой
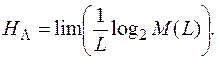
Дата добавления: 2016-02-13; просмотров: 2014;
