Расстояние единственности.

При дешифровании криптограмм может возникнуть ситуация в которой несколько найденных ключей дают осмысленный текст. Например криптограмму WNAJW, полученную при помощи шифра Цезаря порождают два открытых текста RIVER и ARENA, отвечающих величинам сдвига (ключам) 5 и 11 соответственно. Из этих ключей один является истинным, а другой ложным. Найдем оценку для числа ложных ключей. Для этого рассмотрим связь между энтропиями вероятностных распределений P(X), P(K), P(Y), заданных на компонентах X, K, Y произвольного шифра S_в см. лекция 2.

Назовем условную энтропию H(K / Y) неопределенностью шифра S_в по ключу. Она измеряет среднее количество информации о ключе, которое дает шифртекст. Аналогично вводится неопределенность шифра по открытому тексту H(X / Y). Эти величины являются мерой теоретической стойкости шифра.

Минимально возможным значением неопределенности H(X/Y) является 0.

,

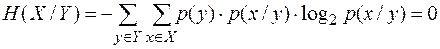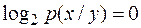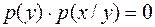это возможно только в тех случаях, когда или для всех x, y, то есть если 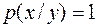при некоторых x, y. Это означает, что по данному y можно получить существенную информацию об x, что свидетельствует о слабости шифра. Идеальной является ситуация когда H(X / Y) = H(X). Именно в этом случае шифр можно было бы назвать совершенным.

Связь между энтропиями компонент шифра дает формула неопределенности шифра по ключу:

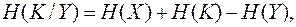
полученная К. Шенноном. Эта формула позволяет получить оценку среднего числа ложных ключей.

Введем обозначение K(y) = {k Î K : $x Î X, E_k(x) = y} – множество ключей, для каждого из которых y является результатом зашифрования некоторого осмысленного текста длины L. Если мы располагаем криптограммой y, то число ложных ключей равно |K(y)| - 1, так как лишь один из допустимых ключей является истинным. Определим среднее число ложных ключей к_L (относительно всех возможных шифртекстов длины L) формулой

.

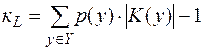Теорема. Для любого рассматриваемого шифра S_в с равновероятными ключами при достаточно больших значениях L в алфавите из n букв имеет место неравенство

.

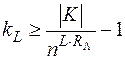где R_L - избыточность данного языка.

Назовем расстоянием единственности для шифра S_в натуральное число L₀, для которого ожидаемое число ложных ключей к_L равно нулю. По сути, расстояние единственности есть средняя длина шифртекста, необходимая для однозначного восстановления истинного ключа (без каких-либо временных ограничений на время его нахождения).

Непосредственно из предыдущего неравенства следует, что

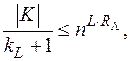
откуда при к_L = 0 получаем 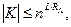и, следовательно,

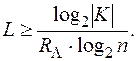
Минимально возможное значение в этом неравенстве и принимается за L₀. Таким образом.

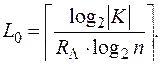
Например для шифра простой замены с параметрами n = 26, |K| = 26!, R_L = 0,5 (примерно соответствует английскому языку) получим оценку

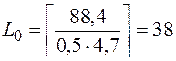
Это значит что для шифра простой замены, для английского языка в среднем по криптограмме длиной около 40 символов можно однозначно определить открытый текст.

Для совершенных шифров типа одноразовых блокнотов расстояние единственности L₀=¥.