Теоретическая стойкость шифров.

При анализе теоретической стойкости шифров отвлекаются от объема реальных затрат на дешифрование. Основным критерием является возможность получения на основе шифртекста вероятностной информации об открытом тексте или используемом ключе. Для теоретически стойких (совершенных) шифров сама задача дешифрования становится бессмысленной. Никакой метод криптоанализа, включая полный перебор ключей, не позволяет не только определить ключ или открытый текст, но даже получить о них какую либо информацию (за исключением длины открытого текста).

Априорная вероятность открытого текста – безусловная вероятность.

Апостериорная вероятность открытого текста – вероятность (по шифртексту) при условии использования соответствующего шифра.

Стойкость по отношению к атаке на основе единственного шифртекста. К. Шеннон назвал шифр совершенным, если шифртекст не дает никакой вероятностной информации об открытом тексте на языке. на языке вероятностной модели 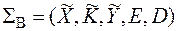, определение совершенного шифра выражается следующим образом:

Определение. Назовем шифр S_в совершенным, если для любых x Î X, y Î Y выполняется равенство

p(x / y) = p_X(x).

Утверждение. Если шифр S_в – совершенный, то

|X| ≤ |Y| ≤ |K|.

Теорема(К. Шеннон).Пусть S_в – шифр, для которого |X| = |Y| = |K|. Тогда шифр S_в – совершенный тогда и только тогда, когда выполняются два условия:

1) Для любых x Î X, y Î Y существует единственный ключ k Î K, для которого

E_k(x) = y;

2) Распределение вероятностей P(K) – равномерное, то есть для любого ключа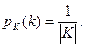

По сути, теорема описывает шифры табличного гаммирования со случайными равновероятными ключами.