Дифференциалды энтропия

Тәжірибе жүзінде ақпарат көзінің мүмкін жағдайларының жиынтығы континуум, яғни үздіксіз қайнар көздерді құрайды.

Үздіксіз ақпарат көзінің энтропиясын келесі түрде анықтаймыз: 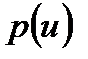ықтималдылығыныңтығыздықүлестірумен сипатталатын 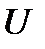, үздіксіз кездейсоқ шаманың өзгеру диапазонын, 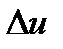ені бар кіші интервалдардың 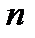ақырғы санына бөлеміз. 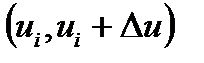интервалына жататын 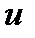-дың кез келген мәнін іске асырғанда, 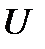дискретті кездейсоқ шаманың, 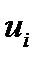мәні іске асырылады деп есептейміз. 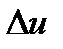кіші болғандықтан, 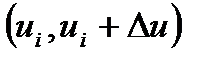интервалынан 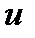мәнінің іске асу ықтималдылығы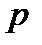 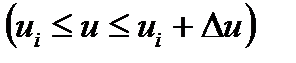төмендегідей:

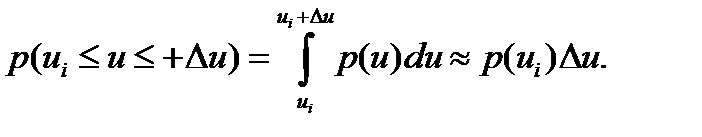
Онда 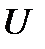дискретті кездейсоқ шаманың энтропиясы келесі түрде жазылуы мүмкін:

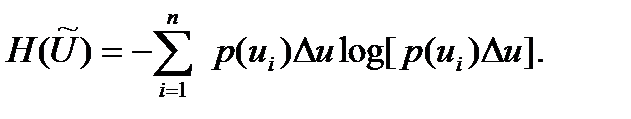
немесе

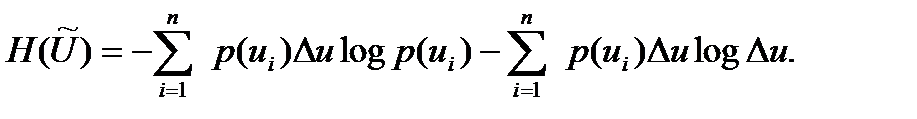
сол себепті

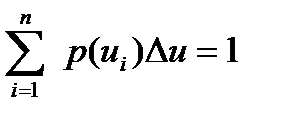
онда

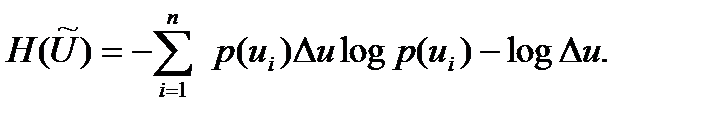
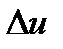кішіреюіне байланысты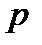 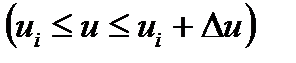, 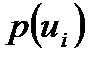ықтималдылығына жақындай түседі, оның мәні нөлге тең. Ал 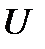дискретті шаманың қасиеті – 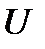үздіксіз кездейсоқ шаманың қасиетіне жақындай түседі. 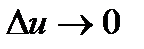шекке көше отырып, 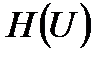үздіксіз қайнар көздің энтропиясы үшін келесідей өрнек аламыз:

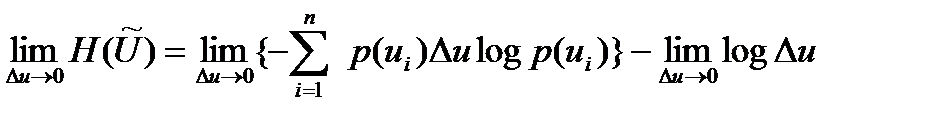
немесе

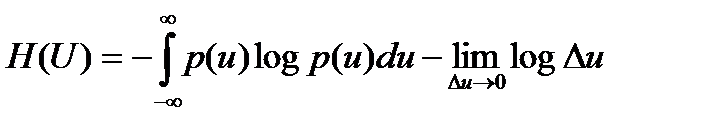(2.8)

Бұл шама 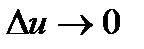жағдайында шексіздікке ұмтылады, ол мүмкін жағдайлардың (мәндердің) шексіз үлкен саннан таңдаудың анықталмағандығы шексіз үлкен деген интуитивті түсінікке толығымен сәйкес келеді.

(2.8) қатынастың оң бөлігінің бірінші мүшесінің ақырғы мәні бар. Ол 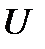үздіксіз кездейсоқ шаманың үлестіру заңына тәуелді және 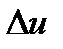кванттау қадамына тәуелді емес. Оның құрылымы дискретті қайнар көздің энтропиясының құрылымындай.

Сол қатынастың екінші мүшесі, керісінше, 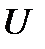кездейсоқ шаманың кванттау қадамына ғана тәуелді, осыған байланысты 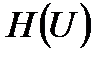шексіздікке ұмтылады.

(2.8) өрнегінің бірінші мүшесін үздіксіз қайнар көздің анықталмағандығы ретінде қабылданылуы, үздіксіз қайнар көздің ақпараттық қасиетінің соңғы сипаттамаларын алу үшін бір қадамы болып табылады:

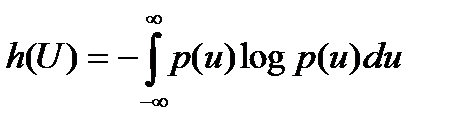(2.9)

Ол салыстырмалы дифференциалды энтропия немесе үздіксіз ақпарат көзінің дифференциалдық энтропиясы деп аталынады ( 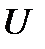кездейсоқ шаманың үздіксіз үлестірілуі).

Оның бірқалыпты үлестіруі бар, диапазоны бірге тең 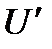кездейсоқ шаманың таңдауының, орташа анықталмағандығыменсалыстырғанда еркін үлестіру заңдылығы бар 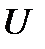кездейсоқ шаманы таңдаудың орташа анықталмағандығы ретінде қарастыруға болады.

Дифференциалды энтропияның қасиеттері:

a) 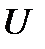кездейсоқ шама үшін оның мүмкін аумағы 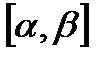жалғыз шектеуі болса, онда бұл аймақта ықтималдылықтарды бірқалыпты үлестіру, максималды дифференциалды энтропияға ие болады;

б) Егер 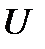үздіксіз кездейсоқ шаманың мәндер аумағына шектеу болмаса, бірақ дисперсияның шектелмегені белгілі болса, онда 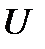шаманың нормальді үлестіруі, максимальды дифференциалды энтропияға ие болады.