ЛЕКЦИЯ №3 .ИСТОЧНИКИ ИНФОРМАЦИИ И ИХ ЭНТРОПИЯ.

3.1 Дискретные источники без памяти и с памятью.

До сих пор мы рассматривали простейшие источники информации, так называемые источники без памяти. Напомним, что дискретный источник без памяти X в каждый фиксированный момент времени выдает некоторый символ 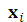из конечного алфавита X= 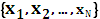с соответствующими вероятностями 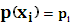, причем выборка символов производится независимо друг от друга. Вот именно для такого источника мы получили информационные меры, в том числе по Шеннону, которые определяется заданной вероятностной схемой сообщения такого источника.

Энтропией дискретного источника без памяти является усредненное на алфавите источника количество информации, приходящееся на один символ, т.е. на одно событие:

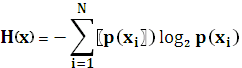, i= .

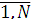Кроме того, нами были получены выражения для совместной условной энтропии пары дискретных источников без памяти, а также выражения для взаимной информации источников.

Кроме рассмотренного, на практике широко применяется понятие стационарного дискретного источника с памятью.

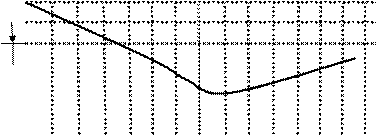
Например, если считать, что выходом источника является дискретизированный аналоговый сигнал (например, речевой), то соседние отсчеты такой дискретизированной последовательности будут как бы взаимосвязаны по времени, т.е. обладают некоторой памятью.

X(t)

t

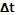
Дискретный источник с памятью Х можно представить как дискретизированный во времени случайный процесс, реализацией которого является последовательность событий x_n, принадлежащих алфавиту источника. И если совместные вероятности этих последовательностей событий x_n не зависят от выбора начальной точки отсчета времени, то дискретный источник с памятью является стационарным. Следовательно, стационарный дискретный источник с памятью математически полностью считается описанным, если известны совместные вероятности 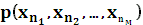для любой выборки 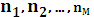, где .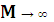

Определение энтропии стационарного дискретного источника с памятью следует из двух подходов, приводящих к одинаковому решению. При первом подходе используют понятие совместной энтропии, при втором - условной энтропии. И это понятно, если учесть, что в энтропии должно быть учтено свойство памяти источника, которое распространяется на некоторую последовательность событий. А это означает, что отдельное событие несет дополнительную информацию, если блок предшествующих событий уже известен. Можно доказать, что энтропия стационарного дискретного источника с памятью можно найти следующим образом:

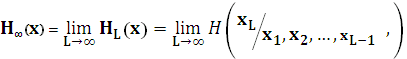
где 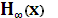- энтропия стационарного дискретного источника с памятью;

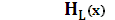– совместная энтропия L последовательных выборок, которые можно рассматривать как самостоятельных L источников, причем последовательных;

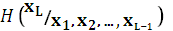- условная энтропия источника 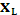при условии, что события предыдущих источников, т.е. до 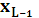, известны.

Для стационарных дискретных источников с памятью используют теорему Шеннона.

Если совместная энтропия стационарных дискретных источников 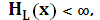то имеют место следующие выражения:

1.

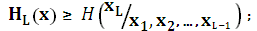
2. 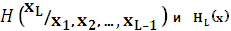не возрастают с ростом длины блока L.

3.2 Эргодические источники.

Все дискретные источники без памяти однозначно относятся к классу эргодических источников. Свойство эргодичности - это постоянство поведения случайного процесса во времени.

Примером такого процесса является бросание монеты или игрального кубика.

Свойство эргодичности процесса позволяет применять операцию усреднения для определения энтропии как среднего количества информации источника. Другими словами, источник будет называться эргодическим, если его вероятностные параметры можно определить по одной достаточно длинной реализации, которую он вырабатывает. В этом случае реализации, по которым можно оценить закон распределения, являются как бы типичными, поэтому эргодические источники можно назвать источниками, которые вырабатывают типичные последовательности. Кроме источника без памяти, свойством эргодичности могут обладать и источники с памятью.

Например, эргодические источники являются наиболее близкими с вероятностной точки зрения моделям осмысленных сообщений, например, источников текстов.

Для эргодических источников справедливы все понятия энтропии, рассмотренной для дискретных источников без памяти. Кроме того, понятия энтропии стационарных дискретных источников, а также совместной и условной его энтропий и их свойств, определенных теоремой Шеннона, имеют место, если стационарный дискретный источник с памятью является эргодическим.

3.3 Марковские цепи

В классе дискретных источников с памятью особое место занимают марковские источники. Их описания базируются на математическом аппарате марковских цепей, с помощью которых можно составить математическую модель многих процессов, наиболее близких к практике.

Значение марковских цепей в теории информации заключается в том, что реальные источники информации вырабатывают сообщения при наличии статистической зависимости между отдельными событиями, символами.

В реальных источниках вероятность выбора какого-либо очередного символа зависит от предшествующих символов.

Марковским процессом называется случайный процесс, у которого будущее состояние определяется только настоящим и не зависит от прошлого. Дискретный по времени и состояниям марковский процесс называется марковской цепью.

Реализацией марковского источника является последовательность состояний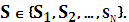

Для описания марковских цепей используют понятия:

1. Множество состояний;

2. Начальное условие (это распределение вероятностей событий в начальный момент времени);

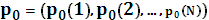
3.Стохастический вектор распределения вероятностей состояний в момент времени n.

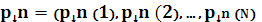, где n=1,2,3,…- дискретные моменты времени.

4.Смена состояний марковских цепей описывается вероятностями перехода

.

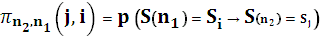5.Переходные вероятности на совокупности состояний в разные моменты времени образуют соответствующие матрицы вероятности перехода.

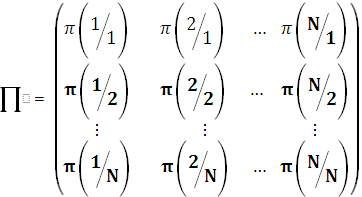
Заметим, что эта стохастическая матрица , в которой сумма вероятностей строк равна 1.Вычисление матрицы вероятности переходов производится с использованием известной рекуррентной формулой, которая является частным случаем уравнения Колмогорова- Чепмена

.

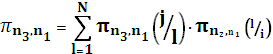Применение марковских цепей достаточно сильно упрощается, когда эти цепи гомогенны, стационарны и регулярны. Марковская цепь называется гомогенной (однородной), если вероятности переходов между состояниями не зависят от выбора временной точки отсчета, т.е. вероятности переходов зависят от разности временных отсчетов, тогда можно записать:

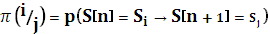, где 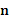=0,1,2,... ;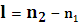

Если 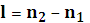; 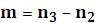, то .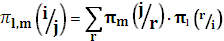

Это выражение может быть представлено в виде суммы компонентных произведений векторов- строк на векторы- столбцы. Записав переходные вероятности виде матриц, получаем матричную запись этого выражения:

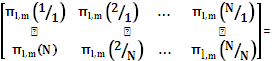
Таким образом, можно получить матрицы переходных вероятностей на любом шаге 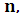многократно применяя указанные выше матричные преобразования к исходному распределению состояний. Тогда можно получить распределение вероятностей 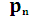на любом шаге, т.е. в любой момент времени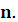

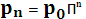
Итак, гомогенная марковская цепь полностью описывается матрицей переходных вероятностей и векторами исходных вероятностей состояний.

Кроме аналитического представления, широко используется и графическое представление марковских цепей.

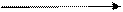
π(j/i)

π(i/j)

Гомогенная марковская цепь является стационарной, если распределение состояний постоянно во времени. В этом случае начальное распределение вероятностей состояний является собственным вектором матрицы переходных вероятностей.

Гомогенная цепь Маркова является регулярной, если:

1. Предельная матрица вероятностей перехода существует.

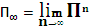
Причем все 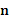строк предельной матрицы представляют собой предельное распределение вероятностей состояний матрицы.

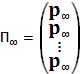
2. Предельное распределение вероятностей состояний 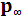является единственным стационарным распределением вероятностей состояний любой регулярной цепи Маркова.

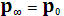
3.Цепь Маркова везде будет регулярной, если существует некоторое натуральное значение шага n, при котором все компоненты некоторого столбца матрицы вероятностей перехода на этом шаге n, будет отлично от нуля. Другими словами, цепь Маркова является регулярной если, на некотором шаге n существует по меньшей мере одно состояние, которое может быть достигнуто из любого начального состояния. Если в марковской цепи вероятность очередного символа оказывает влияние на r предыдущих символов, то говорят, что память такого источника охватывает r последовательных символов, а сам источник называют конечным дискретным марковским источником с памятью r.

Заметим, что такой источник обладает свойством эргодичности. Тогда конечный дискретный эргодический марковский источник с памятью r полностью считается заданным (или определенным ) следующими условиями:

1.Задано непустое множество состояний 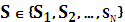, причем каждое состояние 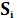содержит вектор длиной r .

2. Каждое состояние 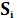соответствует дискретному источнику без памяти с алфавитом 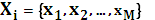и вероятностями j- тых символов алфавита .

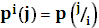3. Задано начальное распределение вероятностей состояний .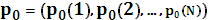

4. Состояние 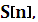образованное из r -1 последовательных символов, после добавления очередного символа 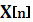переходит в состояние S[n+1].

Энтропия стационарного эргодического марковского источника вычисляется исходя из того, что некоторое состояние источника 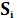является как бы подысточником без памяти, обладающим в свою очередь соответствующей энтропией. Тогда энтропия первоначального источника равна математическому ожиданию энтропии подысточников. Таким образом, стационарный эргодический марковский источник с алфавитом из М символов, имеющий n состояний, т.е. N подысточников без памяти энтропия каждого из которых равна

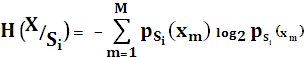, где

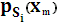- вероятность символа 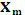при условии 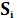состояния, обладает энтропией, равной математическому оживанию энтропии подысточника.

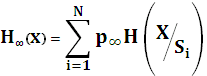, где 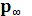- предельное распределение вероятностей состояний.

Строго говоря, это энтропия обладает теми же свойствами, что и дискретный стационарный источник с памятью общего вида.

В теории информации, особенно для связанных источников и источников с памятью, используют понятие информационной дивергенции. Это функция, определяемая для двух распределений вероятностей и характеризующая степень их близости.