Кездейсоқ шаманың эпсилон-энтропиясы.

Шуылы бар дискретті байланыс каналдары бойынша хабарламаны тасымалдағандағы ақпараттық жоғалтулар.

Эпсилон-энтропия

Егер:

1. Ақпарат көзінің жеке жағдайлары дегеніміз 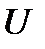кездейсоқ шаманың тәуелсіз іске асуы болып табылады. 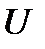кездейсоқ шаманың іске асу ансамблі 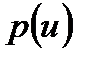ықтималдылығының тығыздық үлестіруімен баяндалады.

2. 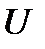кездейсоқ шаманың мәндерін басқа 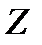кездейсоқ шаманың мәндері бойынша ғана талдауға болады. Олардың айырмашылық өлшемдері берілген өндірілу нақтылығынан аспауы қажет.

3. Дәлділікке қойылатын талаптар 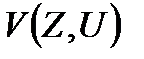критерийін пайдалану арқылы беріледі

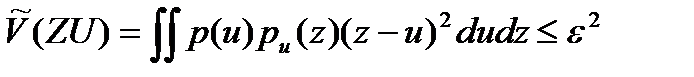(2.10)

мұндағы 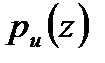– шартты үлестіру тығыздығы – нақты 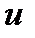сигналы 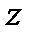сигналы түрінде шығарылуының ақиқаттық функциясы; 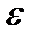– берілген дәлдіктің мәні.

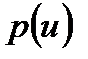тығыздық анықталғандықтан, (2.10) шарты орындалуы үшін 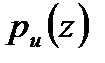үлестірудің шартты тығыздығы арқылы түрлендіруге болады.

Егер 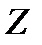кездейсоқ шамасы 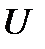қандай да бір 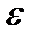дәлдігімен кездейсоқ шаманы туындайтын болса, онда ақпарат саны 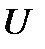–ға қатысты 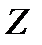туындау шамасында орналасып соңғы болады және келесідей анықталады:

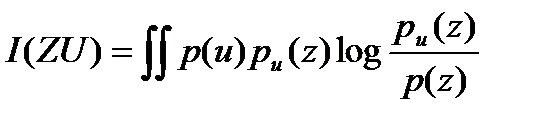(2.11)

Мұндағы 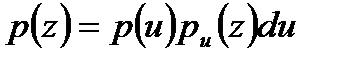– 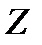туындау шамасының тығыздығы.

Мүмкіндігінше қабылданатын ақпараттың ең кіші санында туындаудың берілген ақиқаттығын қамтамасыз ету. Сондықтанда 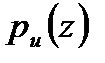, функция жиынтығының арасынан (2.10) шартын қанағаттандыратын, 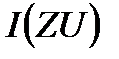-дың ең кішісін қамтамасыз ететін функцияны таңдау қажет.

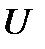-ға қатысты бір 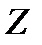кездейсоқ шамасында, 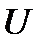шамасының туындау дәлдігіне қойылатын талаптар қанағаттандырылса ең кіші ақпарат саны 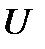шамасының 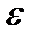(эпсилон) – энтропия шамасы деп аталынады және 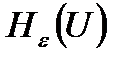деп белгіленеді.

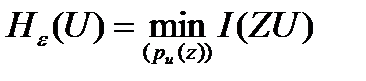, егер

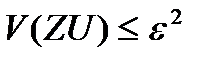(2.12)

Аталмыш шаманың маңыздылығы, 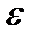(эпсилон) – энтропия берілген нақтылықпен (дәлдікпен) хабарламаны шығару үшін ең кіші екілік сандарды тасымалдау болып табылады.