Алгебраические критерии устойчивости
Простейшим критерием устойчивости является условие положительности коэффициентов характеристического уравнения. Положительность коэффициентов уравнения (8.4) является необходимым (но не достаточным!) условием устойчивости системы. Это означает, что если все коэффициенты положительны, то система может быть устойчивой или неустойчивой. Но если хотя бы один коэффициент уравнения отрицателен или равен нулю, то система неустойчива.
Наиболее распространены в инженерной практике критерий Гурвица.
Критерий Гурвица был сформулирован и доказан в 1895 г. немецким математиком А. Гурвицем, который разработал свой критерий, решая чисто математическую задачу — задачу исследования устойчивости решений линейного дифференциального уравнения. Применительно к задачам теории управления критерий Гурвица можно сформулировать так:
автоматическая система, описываемая характеристическим уравнением 8.5 устойчива, если при а0> 0 положительны все определители D i вида
|
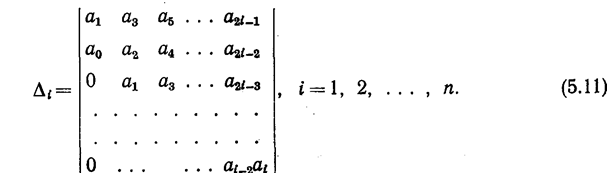
(Как составляется определитель матрицы i * i).
Если хотя бы один из определителей (4.9), называемых определителями Гурвица, отрицателен, то система неустойчива.
Так как последний столбец главного определителя Dn содержит всегда только один элемент an, отличный от нуля, то согласно известному свойству определителей Dn = an Dn-1.
Если главный определитель Dn == 0, а все остальные определители положительны, то система находится на границе устойчивости. С учетом выражения (4.12) это условие распадается на два: an = 0 и Dn-1 = 0.
Условию аn. = 0 соответствует один нулевой корень, т. е. апериодическая граница устойчивости, а условию Dn-1 = 0 - пара мнимых корней, т. е. колебательная граница устойчивости.
Критерий Гурвица целесообразно применять для анализа устойчивости систем не выше пятого порядка. При п > 5 вычисление определителей становится громоздким.
Преимуществом критерия Гурвица является то, что с его помощью можно оценивать устойчивость как замкнутых, так и разомкнутых систем. Вывод об устойчивости при применении этого критерия делается применительно к той системе (замкнутой или разомкнутой), уравнение которой анализируется.
Недостатком является малая наглядность.
Дата добавления: 2016-04-22; просмотров: 1255;
