Общее описания и свойства
Типовые звенья описываются уравнением
a0y'' (t) + a1y' (t) + a2y(t) = b0x' (t) + b1x(t). (1)
Принято приводить уравнение звена к стандартному виду в символической записи:
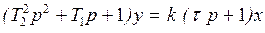 , (2)
, (2)
где T22 =a0/a2; T1 = a1/a2; t =b0/b1 - постоянные времени; k = b1/a2.
Вспомним, как можно получить характеристики звеньев:
-статические, приравнивая производные по времени к нулю,
-динамические: … .
W(p) = R(p) /Q(p) =k(tp+1)/( T22 p2 +T1 p +1) , (2)
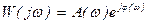 , (2)
, (2)
Для получения переходной характеристики h(t) ищется общее решение, состоящее из двух частей. Импульсная характеристика является производной по времени от переходной характеристики w(t) = dh(t)/dt.
Из общего вида уравнения или передаточной функции можно сделать некоторые выводы о свойствах звеньев. Если коэффициенты a2 и b1 не равны нулю, то такие звенья называются статическими или позиционными, что говорит о наличии уравнения статики. В противном случае звенья являются астатическими n-го порядка, где n – это степень при операторе дифференцирования, характеризующего астатизм звена или системы.
Ряд звеньев называются элементарными, а именно безынерционные, идеально дифференцирующие и идеально интегрирующие.
виде
Обзор и примеры
Таблица 3.1

Таблица 3.2Временные характеристики позиционных звеньев
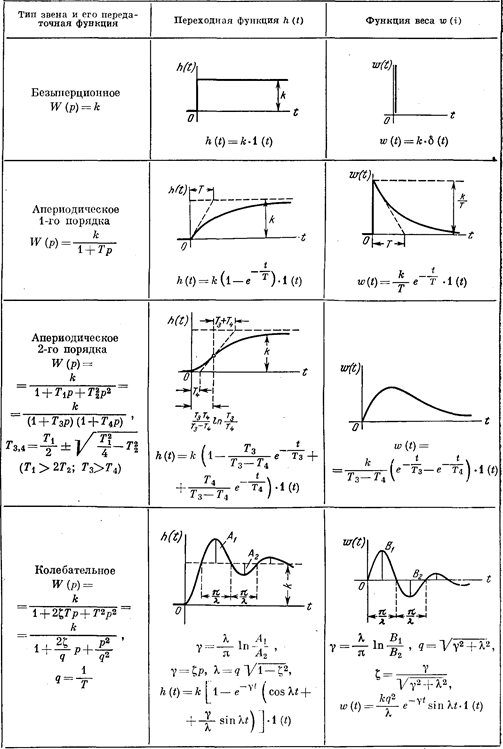
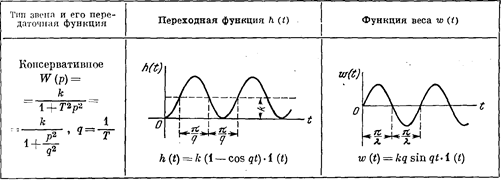
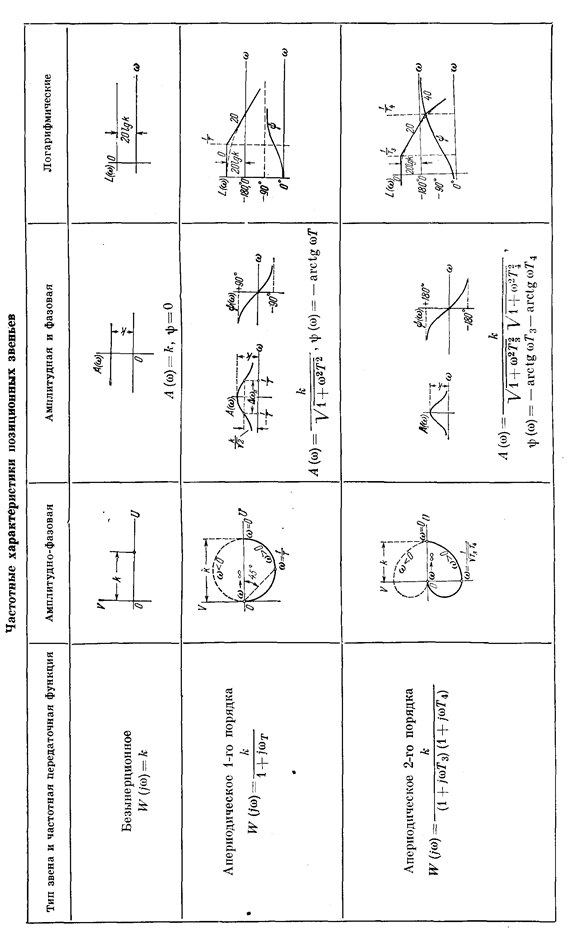
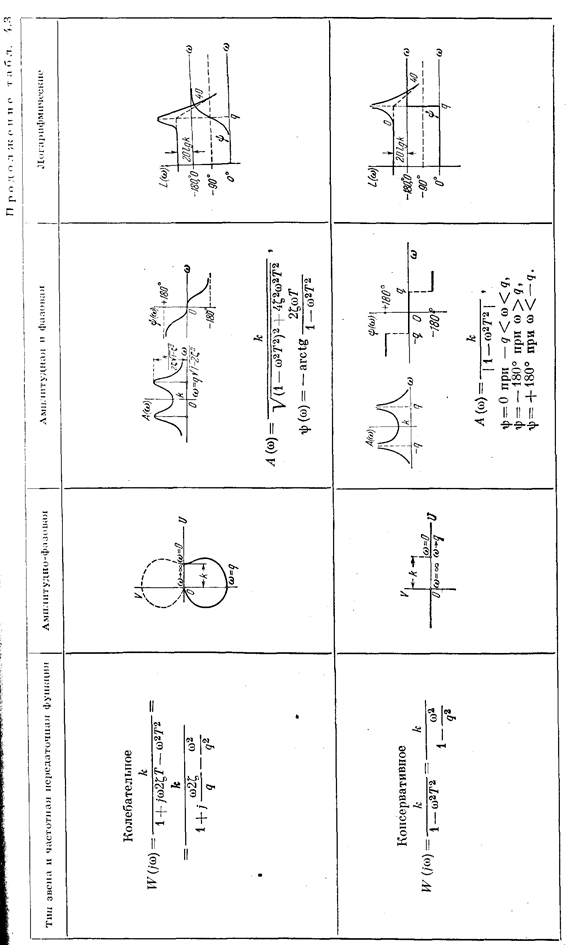
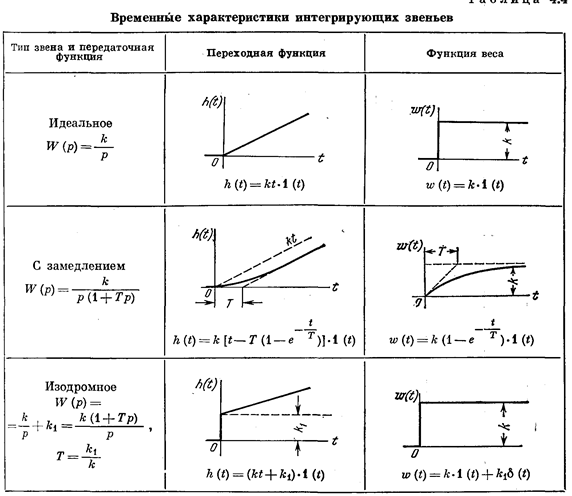
Таблица 3.6
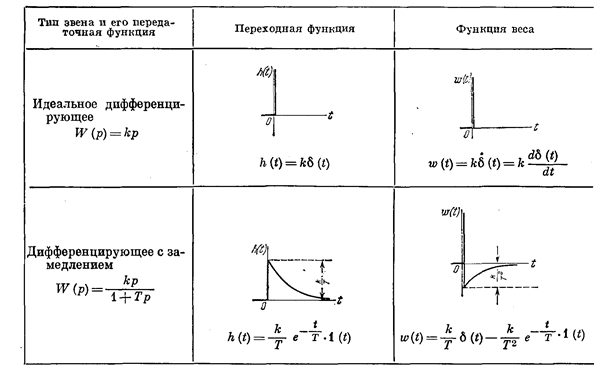
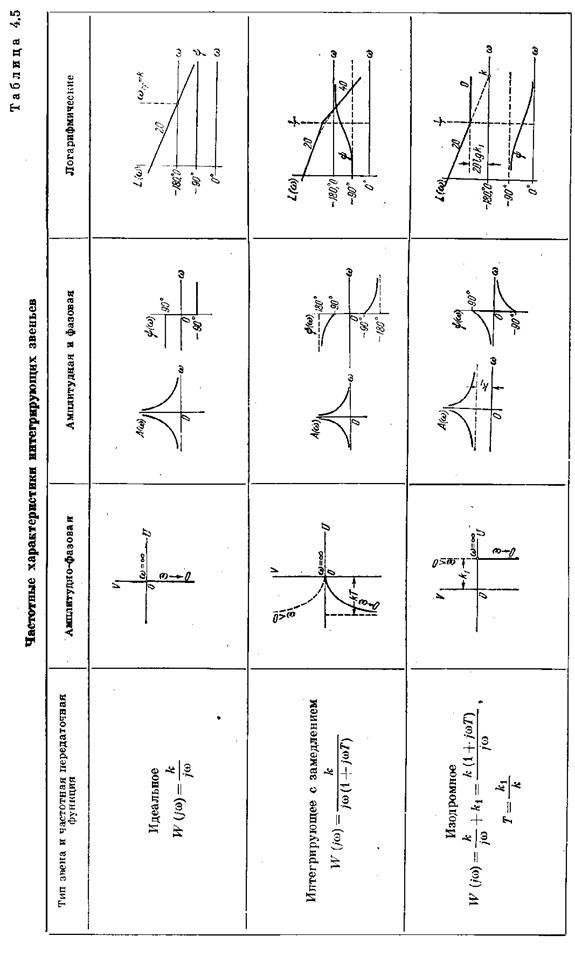
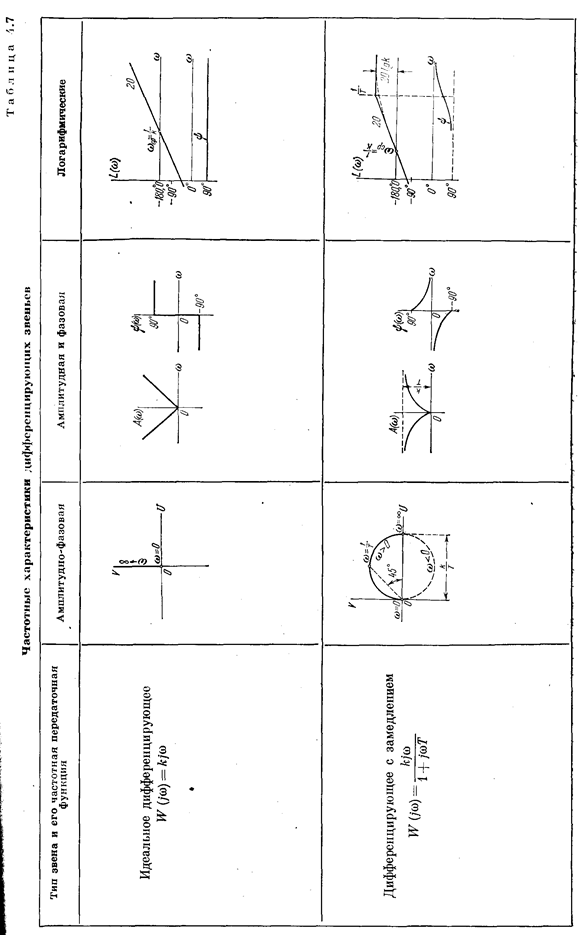
Временные характеристики дифференцирующих звеньев
ЛЕКЦИЯ № 4
Дата добавления: 2016-04-22; просмотров: 977;
