Модели регрессии по временным рядам с лаговыми переменными принято называть динамическими моделями. Их можно подразделить на три класса
1. Модели с лаговыми объясняющими переменными — модели с распределенными лагами
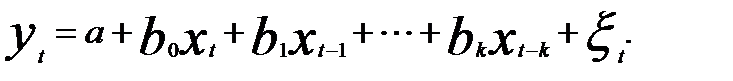 (5.34)
(5.34)
2. Модели с лаговыми зависимыми переменными — модели авторегрессии
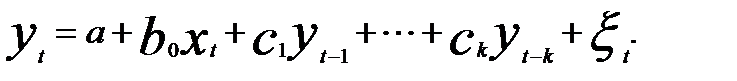 5.35)
5.35)
3. Модели с лаговыми зависимыми и независимыми переменными — авторегрессионные модели с распределенными лагами
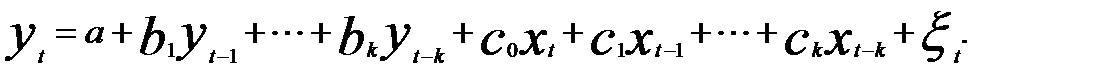 (5.36)
(5.36)
Центральным вопросом при построении моделей с лаговыми переменными является выбор величины лага и числа лаговых переменных. Теоретически трудно определить величину лага. Определенную помощь может оказать взаимная корреляционная функция: рассчитывается множество коэффициентов корреляции между уровнями временных рядов 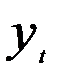 и
и 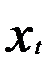 , сдвинутыми относительно друг друга на последовательно увеличивающиеся интервалы времени. Величина лага определяется по максимальному значению коэффициента корреляции. Например, продажа товара за две декады двумя филиалами фирмы характеризуется данными, представленными в таблице (тыс. ден. ед.).
, сдвинутыми относительно друг друга на последовательно увеличивающиеся интервалы времени. Величина лага определяется по максимальному значению коэффициента корреляции. Например, продажа товара за две декады двумя филиалами фирмы характеризуется данными, представленными в таблице (тыс. ден. ед.).
| Числа месяца | Филиал № 1 | Филиал № 2 | Числа месяца | Филиал № 1 | Филиал № 2 | |
| 9,5 | ||||||
| 4,5 | 10,8 | |||||
| 13,5 | 7,6 | |||||
| 4,1 | 14,5 | 7,5 | ||||
| 7,6 | ||||||
| 14,7 | ||||||
| 12,2 | ||||||
| 9,7 | 26,3 | |||||
| 11,9 | 15,6 | 26,4 | ||||
| 27,1 |
Примем объем продаж филиалом № 1 за 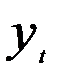 , а филиалом № 2 — за
, а филиалом № 2 — за 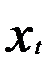 . Если прокоррелировать
. Если прокоррелировать 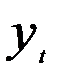 и
и 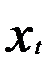 , то коэффициент корреляции между ними составит 0,6912. При последовательном сдвиге уровней ряда
, то коэффициент корреляции между ними составит 0,6912. При последовательном сдвиге уровней ряда 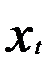 на один временной интервал получатся коэффициенты корреляции, представленные в следующей таблице.
на один временной интервал получатся коэффициенты корреляции, представленные в следующей таблице.
| Величина лага | ||||||
| 0,7738 | 0,867 | 0,9445 | 0,9553 | 0,8562 | 0,5977 | 0,0724 |
Следовательно, объем продаж филиалом № 1 в наибольшей мере коррелирует с объемом продаж по филиалу № 2 с интервалом в 4 дня. Уравнение регрессии принимает вид 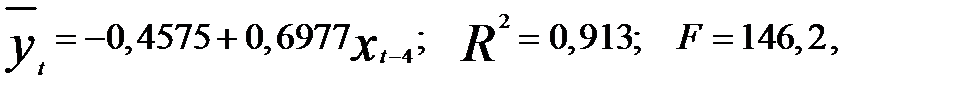 что статистически значимо. Оно позволяет по данным филиала № 2, взятым на четыре дня раньше, предсказывать объем продаж по филиалу № 1. Так, например, при объеме продаж за 2-е число в 10,8 тыс. ден. ед. по филиалу № 2 объем продаж по филиалу № 1 составит 6-го числа 7,1 тыс. ден. ед. Соответственно подставляя в уравнение регрессии информацию об объеме продаж филиалом № 2 за 3—16-е числа, получим объем продаж по филиалу № 1 на 7—20-е числа.
что статистически значимо. Оно позволяет по данным филиала № 2, взятым на четыре дня раньше, предсказывать объем продаж по филиалу № 1. Так, например, при объеме продаж за 2-е число в 10,8 тыс. ден. ед. по филиалу № 2 объем продаж по филиалу № 1 составит 6-го числа 7,1 тыс. ден. ед. Соответственно подставляя в уравнение регрессии информацию об объеме продаж филиалом № 2 за 3—16-е числа, получим объем продаж по филиалу № 1 на 7—20-е числа.
Выбор величины лага и количества лагов проводится обычно экспериментально: строятся модели с разным числом лагов и их величиной и изучается значимость коэффициентов регрессии при лаговых переменных; останавливаются на модели, для которой все коэффициенты регрессии при лаговых переменных будут статистически значимыми по t-критерию Стьюдента.
Построение моделей с лаговыми переменными имеет свою специфику. Дело не только в выборе величины лага и их числа. Во многих случаях оценка параметров моделей с лаговыми переменными не может быть проведена с помощью традиционного МНК ввиду нарушения ряда его предпосылок и требует специальных методов оценивания. При наличии двух и более лаговых переменных возникает проблема мультиколлинеарности факторов, ибо, как правило, 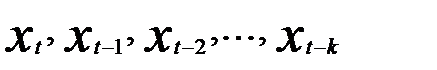 или
или 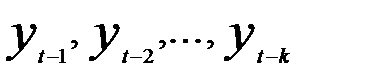 связаны между собой, особенно при наличии тенденции в рядах динамики. Это снижает точность оценок коэффициентов при лаговых переменных и требует видоизменять приемы оценивания.
связаны между собой, особенно при наличии тенденции в рядах динамики. Это снижает точность оценок коэффициентов при лаговых переменных и требует видоизменять приемы оценивания.
Дата добавления: 2016-03-22; просмотров: 1638;
