Алгоритмы работы с рядами

При работе с рядами обычно составляют рекуррентную формулу, которая задает значение i+1-го члена ряда (Y(i+1)) через значения пре­ды­ду­щих членов, чаще ‑ i-го члена ряда (Y(i)). Обычно используют отношение i+1-го чле­на к i-му члену, подставляют их значения, и после преоб­ра­зо­ва­ний полу­чает­ся рекуррентная формула.

Пример. Вычислить значение членов бесконечного ряда 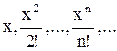точностью до члена 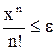. Считать, что требуемая точ­ность (ε) достигнута, если очередное слагаемое по модулю меньше ука­зан­ной точности и все последующие слагаемые можно уже не учитывать. Опре­де­лим рекуррентную формулу Y(i+1)/Y(i)=(x⁽ⁱ⁺¹⁾/(i+1)!)/(xⁱ/i!)=x/i. Получим рекуррентную формулу Y(i+1)=Y(i)*x/(i+1).

1.Вычислить сумму членов для следующих рядов с точностью до 10^-4:

а)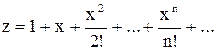

б)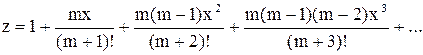

Для вычисления текущего значения члена ряда использовать рекуррентную формулу 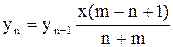, где n ‑ номер члена ряда. Начальное значение у принять равным ;

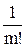в) ;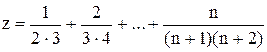

г) ;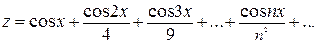

д) ;.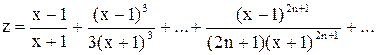

е) ;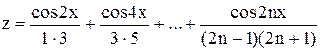

ж) .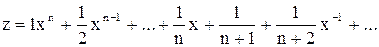

Текущий член ряда вычислять, используя рекуррентную формулу.

2.Составить программу вычисления значений членов убывающей последовательности 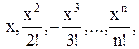… с точностью до10^-4.

3.Составить программу вычисления членов бесконечного ряда

z =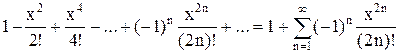

с точностью до10^-4.

4.Не используя стандартные функции (за исключением abs), вычислить с точностью до 10^-4:

а)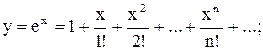

б)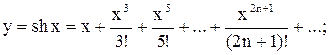

в)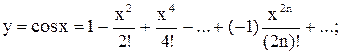

г)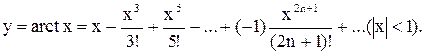

5.Вычисление f = 10!

6.Вычислить:

а) у = cos(x )+ cos(x²) + cos(x³) +…+cos(x³⁰);

б) у = 1! + 2! + 3! + …+ n! (n>1);

в) у ‑ первое из чисел sin(x), sin(sin(x)), sin(sin(sin(x,…))), меньшее по модулю 10^-4.

7.Числа Фибоначчи («f_n») определяются по формулами f₀ = f₁ = 1;

f_n = f_n-1 + f_n-2 при n = 2, 3, …:

а) определить четвертое число Фибоначчи;

б) вычислить первое число Фибоначчи, большее m (m > 1);

в) вычислить s ‑ сумму всех чисел Фибоначчи, которые не превосходят 1000.

* Дочерняя таблица должна иметь первичный ключ.

* Во всех тригонометрических функциях угол задается в радианах.