Моделирование основной тенденции

Рассмотренные приемы выявления общей тенденции изменения динамического ряда не позволяют получить описание плавной линии развития (тренда) данного ряда. Для этой цели используется аналитическое выравнивание, сущность которого заключается в нахождении уравнения, выражающего закономерность изменения явления как функцию времени .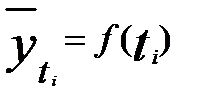

Вид уравнения определяется характером динамики развития конкретного явления.

Логический анализ при выборе вида уравнения может быть основан на рассчитанных показателях динамики, а именно:

• если относительно стабильны абсолютные приросты (первые разности уровней приблизительно равны), сглаживание может быть выполнено полиномом первой степени;

• если абсолютные приросты равномерно увеличиваются (вторые разности уровней приблизительно равны), можно принять полином второй степени;

• при ускоренно возрастающих (замедляющихся) абсолютных приростах принимают полином третьей степени;

• при относительно стабильных темпах роста принимают показательную функцию.

На практике выбор формы кривой может быть основан на анализе графического изображения уровней динамического ряда (линейной диаграммы); при этом целесообразнее воспользоваться графическим изображением сглаженных уровней, в которых случайные колебания погашены. Если условия формирования уровней ряда изменяются, то расчет параметров уравнения не следует вести по данным за весь рассматриваемый период. В этом случае было бы целесообразно разбить ряд динамики на ряд периодов, основываясь на оценке устойчивости показателей динамики.

Ниже приводятся различные виды трендовых моделей, наиболее часто используемых для аналитического выравнивания:

1. Полином первой степени (прямая)

.

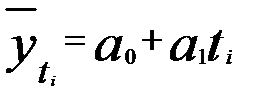2. Полином второй степени (парабола)

.

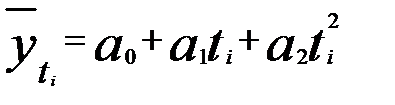3. Полином третьей степени

.

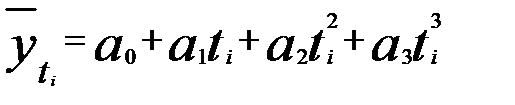4. Показательная

.

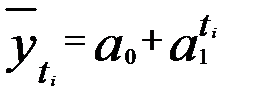5. Гиперболическая

.

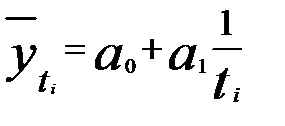По полученной модели для каждого периода (каждой даты) определяются теоретические уровни тренда ( 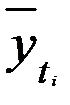) и стандартная ошибка аппроксимации (среднее квадратическое отклонение тренда) по формуле

,

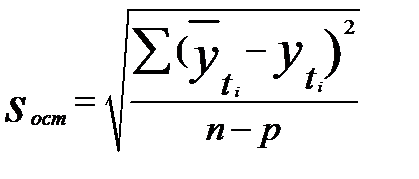где 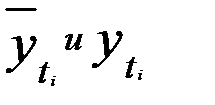— соответственно расчетные и фактические значения уровней динамического ряда; n — число уровней ряда;

p — число параметров в уравнении тренда.

Аналитическое сглаживание позволяет не только определить общую тенденцию изменения явления на рассматриваемом отрезке времени, но и выполнять расчеты для таких периодов, в отношении которых нет исходных данных.

Нахождение по имеющимся данным за определенный период времени некоторых недостающих значений признака внутри этого периода называется интерполяцией. Нахождение значений признака за пределами анализируемого периода называется экстраполяцией.

Применение экстраполяции для прогнозирования должно основываться на предположении, что найденная закономерность развития внутри динамического ряда сохраняется и вне этого ряда. Это означает, что основные факторы, сформировавшие выявленную закономерность изменения уровней ряда во времени, сохранятся и в будущем.

При составлении прогнозов уровней социально-экономических явлений обычно оперируют не точечной, а интервальной оценкой, рассчитывая так называемые доверительные интервалы прогноза. Границы интервалов определяются по формуле

,

,

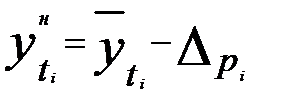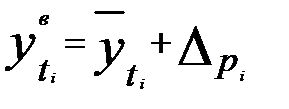где 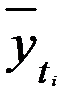, — точечный прогноз, рассчитанный по модели;

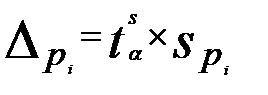— ширина доверительного интервала прогноза;

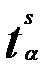— коэффициент доверия по распределению Стьюдента при уровне значимости ;

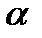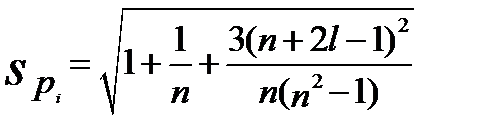— средняя квадратическая ошибка прогноза;

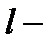период упреждения прогноза.