Компоненты динамического ряда

Модели по рядам динамики могут строиться на основе:

— изолированного динамического ряда, т.е.изучается один динамический ряд, например по данным о численности занятых за несколько лет строится модель динамики чис­ленности занятых;

— системы взаимосвязанных рядов динамики, т.е.когда один из рядов рассматривается как моделируемый объект, а другие — как его факторы, например строится модель прибыли в зависимости от объема реализации, числен­ности работающих, фондовооруженности труда и т.п.

При построении моделей по временным рядам необходи­мо учитывать компоненты (составные части) динамическо­го ряда.

Уровни динамического ряда в конкретный период време­ни t принимают те или иные значения в результате действия разных факторов. Одни из них являются основными, форми­рующими величину уровняy_t на данном этапе исторического развития, а другие — случайными, несущественными с точки зрения содержания его материальной природы. Фактическую величину уровня динамического ряда y_t можно представить как функцию трех компонент:

— тенденции ряда, обусловленной влиянием общих фак­торов, определяющих основное направление разви­тия явления за длительный период времени — тренд ряда;

— периодических колебаний, вызванных особенностями существования явления в одни периоды по сравнению с другими (циклические — период колебаний несколь­ко лет, сезонные — внутригодичные колебания);

— случайных колебаний, связанных с действием разного рода второстепенных факторов, — случайная компонен­та.

Символически функцию можно представить в виде

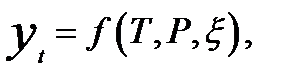
где y_t — фактический уровень динамического ряда в период време­ни t; Т — тренд ряда; Р — периодические колебания (циклические, сезонные); 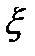—случайная составляющая.

Рассматриваемые компоненты динамического ряда нео­бязательно присущи каждому временному ряду. Могут быть ряды динамики, в которых отсутствуют как тенденция, так и периодические колебания. В этом случае уровни ряда яв­ляются функцией случайной компоненты: y_t = f( 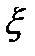). Они ко­леблются вокруг среднего уровня, что характерно для так называемого стационарного ряда.

Такие ряды в экономике сравнительно редки. Чаще имеют место ряды с тенденцией. В основном ряды без тенденции на­блюдаются при изучении динамики показателей из относи­ относи­тельных и средних величин.

Большинство динамических рядов в экономике характери­зуются тенденцией и случайными колебаниями. Модель уровня такого ряда имеет вид

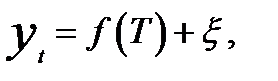
где 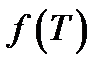— математическая функция, характеризующая закономер­ность развития явления во времени, т.е. описывающая тенденцию развития явления — тренд ряда; 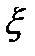— случайные колебания.

При изучении динамики явления за продолжительный пе­риод времени уровни ряда могут обнаруживать регулярные колебания, повторяющиеся через равные промежутки време­ни: спады или подъемы. Такие колебания принято называть периодическими).

Если период колебаний насчитывает несколько лет, то такие периодические колебания считают циклическими. Например, солнечная активность проявляется с периодом 10—11 лет. В сфере предпринимательства могут иметь ме­сто экономические циклы, включающие в себя рост, спад, свертывание и затем оживление экономической деятель­ности. Длина цикла зависит от вида деятельности и охва­тывает нередко 3—12 лет

Регулярные колебания в течение года называются сезонны­ми (обозначаются S). Например, к сезонным относятся коле­бания спроса на одежду с изменением сезона года (весна, лето, осень, зима), колебания цен на сельскохозяйственную продук­цию и т.п. Цикл колебаний равен году. Наличие сезонных ко­лебаний означает, что на протяжении ряда лет в одни и те же кварталы (месяцы) года наблюдается рост или снижение уров­ня ряда. Так, рождественские праздники обусловливают рост товарооборота в декабре и январе.

В отличие от периодических случайные колебания не но­сят регулярный характер и связаны с действием разного рода случайных причин.

Рассматриваемые компоненты динамического ряда позво­ляют представить уровень динамического ряда в виде адди­тивной или мультипликативной моделей:

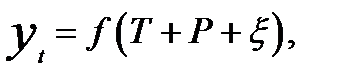—аддитивная модель;

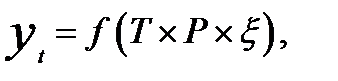—мультипликативная модель.

Выбор вида модели зависит от характера периодических колебаний. Если амплитуда, например, сезонных колебаний остается во времени постоянной, то применяется аддитивная модель. Если же амплитуда колебаний изменяется во времени, то рассматривается мультипликативная модель.

Рассмотренные компоненты динамического ряда учитыва­ются как при построении модели изолированного временного ряда, так и при построении регрессионных моделей на осно­ве системы взаимосвязанных рядов динамики, что будет из­ложено далее.