Порядковое условие идентификации

В общем случае отдельное структурное уравнение системы является идентифицируемым, если имеется достаточное количество экзогенных переменных, не включенных в само уравнение, которые можно использовать как инструментальные для всех эндогенных объясняющих переменных уравнения.

В полностью определенной модели будет столько уравнений сколько имеется эндогенных переменных.

Пусть D — число не включенных в уравнение, но присутствующих в системе экзогенных переменных, а G — число включённых в уравнение эндогенных переменных.

Необходимое условие идентификации. Уравнение в структурной модели может быть идентифицировано, если число не включённых в него экзогенных переменных не меньше числа включённых в его объясняющих эндогенных переменных, т.е.

D≥G -1 (порядковое условие).

Данное условие является необходимым, но недостаточным для идентификации.

В частности:

• если D= G - 1, то уравнение точно идентифицируемо;

• если D>G- 1, то уравнение сверхидентифицируемо;

• если D < G - 1, то уравнение неидентифицируемо.

Достаточное условие идентификации. Уравнение идентифицируемо , если ранг матрицы, составленной из коэффициентов при переменных (эндогенных и экзогенных), отсутствующих в исследуемом уравнении, не меньше N- 1, где N — число переменных системы.

Пример 3. Проверим на идентификацию каждое уравнение модели

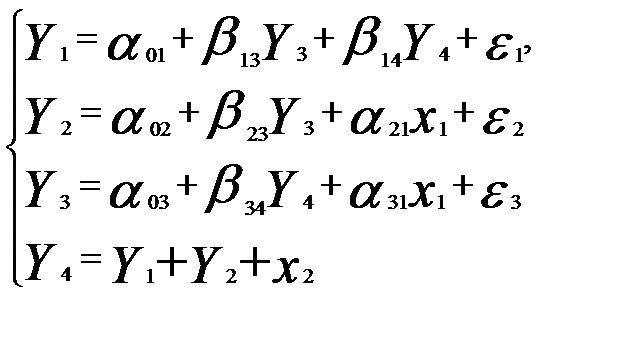
где 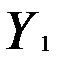— расходы на потребление текущего года; 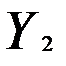— валовые инвестиции в текущем году; 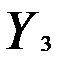— расходы на заработную плату в текущем году; 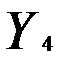— валовой доход за текущий год; 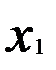— валовой доход предыдущего года; 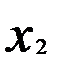— государственные расходы текущего года; 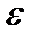— случайные ошибки.

В данной модели четыре эндогенные переменные ( 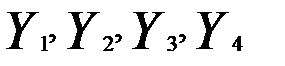), т.е. N= 4, и две экзогенные ( ).

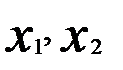Для первого уравнения: (G= 3 ( 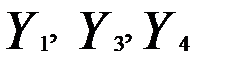присутствуют), D = 2 ( 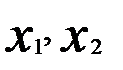отсутствуют) и D = G - 1, поэтому уравнение точно идентифицируемо (необходимое условие).

Для проверки на достаточное условие идентификации выпишем матрицу А коэффициентов при переменных, не входящих в первое уравнение:

Определитель матрицы 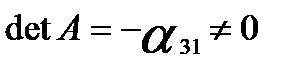, следовательно, ранг матрицы равен 3 >N- 1, т.е. достаточное условие идентификации выполняется, и первое уравнение точно идентифицируемо.

Второе уравнение системы также точно идентифицируемо: G= 2, D= 1 и D = G - 1.

Выпишем матрицу А коэффициентов при переменных, не входящих во второе уравнение:

Выполняется также достаточное условие идентификации: 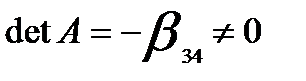, ранг матрицы равен 3 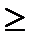N- 1.

Аналогично третье уравнение системы точно идентифицируемо: G= 2, D= 1, D = G- 1.

Выпишем матрицу А коэффициентов при переменных, не входящих во третье уравнение:

Здесь также выполняется достаточное условие идентификации detA = 1, ранг матрицы равен 3 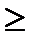N - 1

Четвертое уравнение представляет собой тождество, параметры которого известны, поэтому необходимости в его идентификации нет.

Таким образом, все уравнения модели точно идентифицированы.

Пример 4. Выполним идентификацию следующей модели:

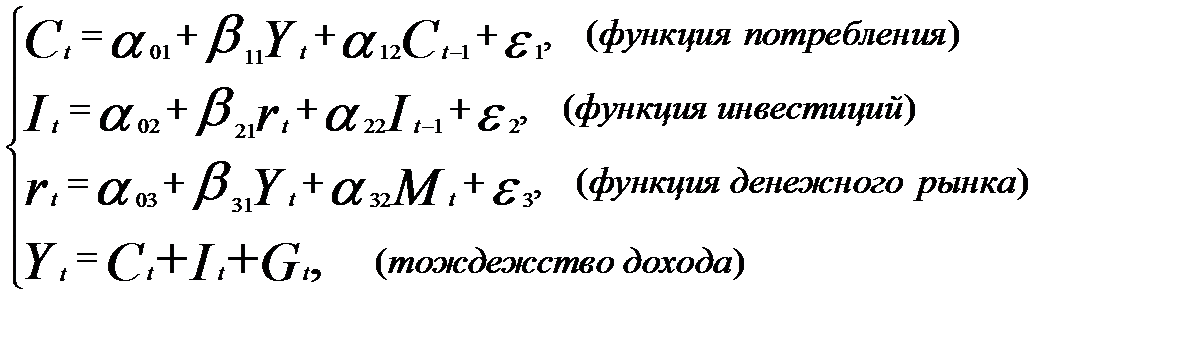
где С — расходы на потребление; Y— совокупный доход; I — инвестиции; r— процентная ставка; М — денежная масса; G — государственные расходы; t — текущий период; t-1— предыдущий период.

В данной модели четыре эндогенные переменные ( 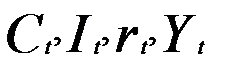), т.е. N= 4, и четыре экзогенные ( ).

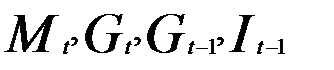Для первого уравнения: G = 2 ( 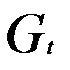и 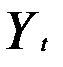присутствуют), D = 3 ( 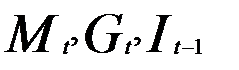отсутствуют) и D>G- 1, поэтому уравнение сверхидентифицируемо (необходимое условие).

Для проверки на достаточное условие идентификации выпишем матрицу коэффициентов при переменных, не входящих в первое уравнение:

Минор третьего порядка данной матрицы

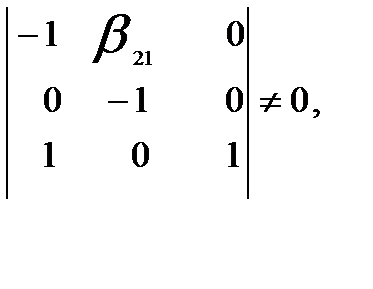
следовательно, ранг матрицы равен 3 >N- 1, т.е. достаточное условие идентификации выполняется.

Для второго уравнения: G = 2 ( 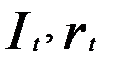присутствуют), D = 3 ( 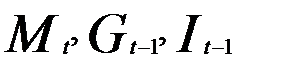отсутствуют) и D>G- 1, поэтому уравнение сверхидентифицируемо.

Выпишем матрицу коэффициентов при переменных, не входящих во второе уравнение:

Минор третьего порядка данной матрицы

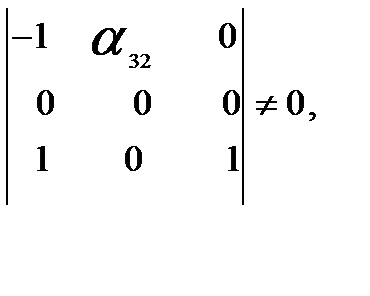
следовательно, ранг матрицы равен 3 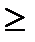N-l, т.е. достаточное условие идентификации выполняется.

Для третьего уравнения: G=2( 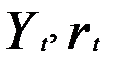присутствуют), D = 3 ( 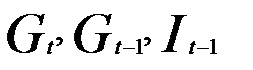отсутствуют) и D>G- 1, поэтому уравнение сверхидентифицируемо.

Выпишем матрицу коэффициентов при переменных, не входящих в третье уравнение:

Минор третьего порядка данной матрицы

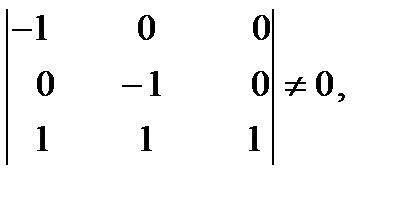
следовательно, ранг матрицы равен 3 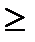N- 1, т.е. достаточное условие идентификации выполняется.

Четвертое уравнение представляет собой тождество, параметры которого известны, поэтому необходимости в его идентификации нет.

Таким образом, все уравнения модели сверхидентифицированы.