Ненулевое ограничение

Добавление экзогенной переменной не единственный способ, который может привести к идентифицируемости уравнения. В некоторых случаях неидентифицируемая модель может быть идентифицируема путем задания соотношения между структурными коэффициентами.

Рассмотрим неидентифицируемую модель спроса и предложения (10). Улучшим спецификацию модели, введя ограничение на коэффициенты :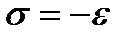

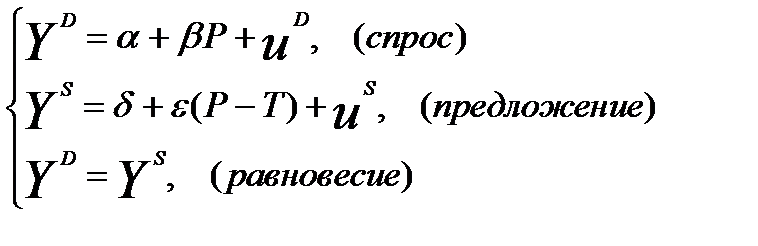(13)Благодаря введению ограничения на коэффициенты уравнение предложения также стало идентифицируемым. Действительно, при использовании ИП можно рассмотреть новую версию модели как систему из четырех уравнений:

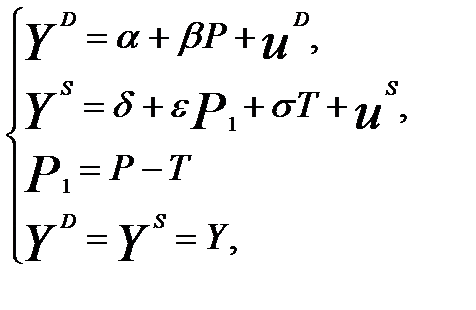(14)

где 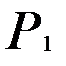— цена товара для продавца (сумма, остающаяся у него после уплаты налога).

Последние два уравнения системы (14) являются уравнениями-тождествами и не требуют проверки на идентификацию. ПеременнаяТ не включена в уравнение спроса, поэтому она может использоваться как инструментальная для Р. Точно так же эта переменная не включена в уравнение предложения, поэтому она может использоваться как инструментальная для .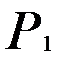

В итоге модель в целом является точно определенной {точно идентифицируемой).

Вывод. Ненулевое ограничение позволяет исключить одну объясняющую переменную из уравнения. Если эта переменная эндогенная, для нее не нужно искать инструментальную переменную, если экзогенная, то она освобождается на роль инструментальной для одной из эндогенных переменных, оставшихся в уравнении.

Пример 5. Опишем процедуру оценивания структурной модели (13). Модель имеет две эндогенные переменные (Y, Р) и одну экзогенную (Т).

Было показано, что исходная модель точно идентифицируема, и поэтому для оценки ее структурных коэффициентов используем КМНК.

Разрешая исходную систему относительно Y, Р, получим приведенную систему

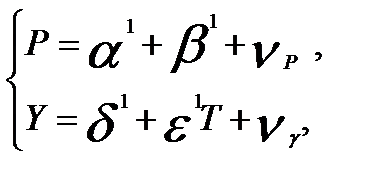
где 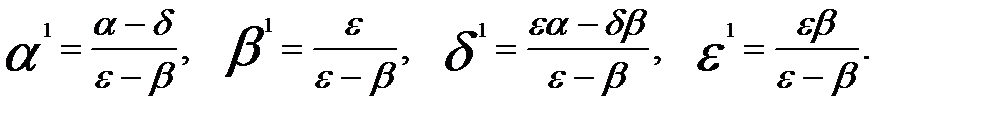(15)

Пусть имеются следующие наблюдения:

Оцененные уравнения приведенной системы, полученные по выборочным данным с использованием МНК, есть

|

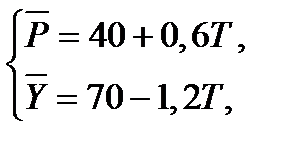т.е. оценки 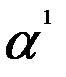= 40, 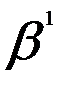= 0,6, = 70, 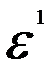= -1,2.

Тогда соотношения (15) имеют вид

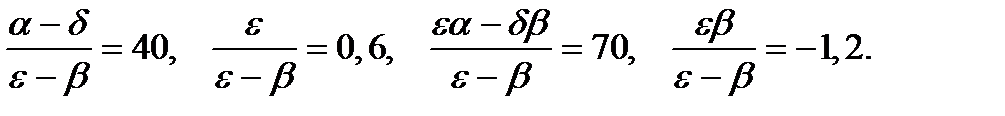
Отсюда получаем следующие оценки структурных коэффициентов:

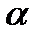= 150, 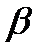= -2, 5, 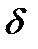= -50, 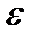=3.

Перейти от приведенной формы модели к структурной с учётом

соотношения (14) можно также следующим образом.

Выразив Т из первого уравнения приведенной формы в виде

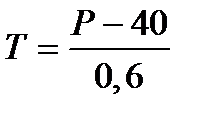и подставив его во второе, получим 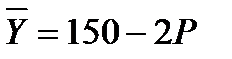, т.е. = 150, = -2.

Выразив Т из первого уравнения приведенной формы в ви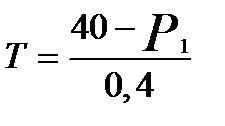де

, где 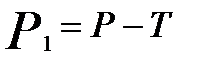, и подставив его во второе, получим 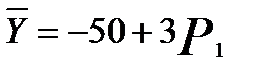, т.е. 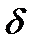= -50, 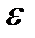= -2.