Неидентифицируемость

Рассмотрим следующую модель спроса и предложения:

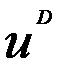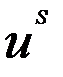где P- цена товара, и - случайные члены.

Переменные Y, Р являются эндогенными, и их значения определяются в процессе установления равновесия.

В рассматриваемой модели нет экзогенных переменных, поэтому ни одно из этих уравнений не является идентифицируемым. Чтобы модель имела статистическое решение, в нее вводятся экзогенные переменные.

Предположим, что продавцы товара облагаются специальным налогом Т, который они должны платить с выручки. При этом уравнение спроса останется неизменным, если переменная Р означает рыночную цену, а уравнение предложения изменится:

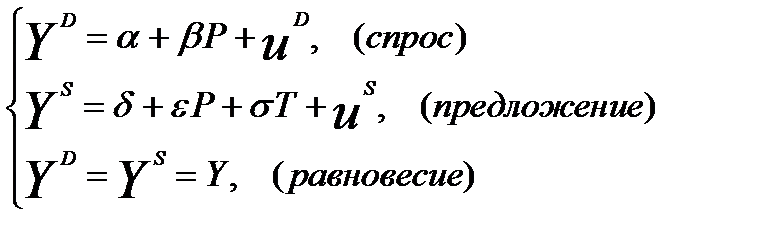(10)

где T – экзогенная переменная.

Уравнение спроса будет идентифицируемым, поскольку переменная Т не включена в него и может выступать как инструментальная для Р, а уравнение предложения — неидентифицируемым.

Включим в уравнение спроса экзогенную переменную х — доход на душу населения:

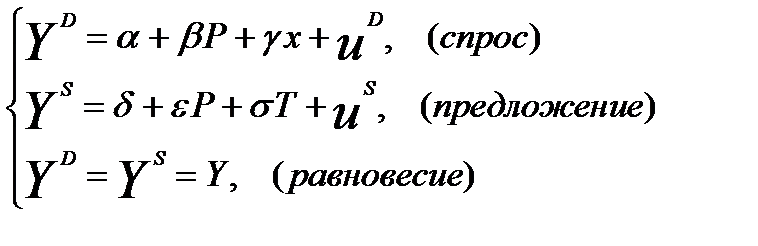(11)Экзогенную переменную х можно использовать как инструментальную вместо Р для уравнения предложения.

В итоге получили в целом точно идентифицируемую модель спроса и предложения.

Пусть структурное уравнение спроса имеет временной тренд (скажем, потому что привычки медленно меняются со временем):

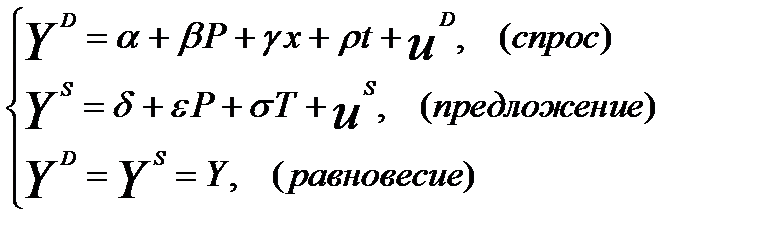(12)

где t — переменная времени, а 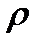— коэффициент при ней.

В модели спроса имеются две экзогенные переменные x, t, которые можно использовать в качестве инструментальных для P в уравнении предложения.

В итоге получили сверхидентифицируемое уравнение предложения и точно идентифицируемое уравнение спроса.