Динамическое условие
Пусть кулачок действует на толкатель с некоторой силой Fд (сила давления). Вектор силы Fд направлен вдоль нормали n-n. (рис.12.6). Угол между направлениями векторов силы Fд и скорости толкателя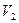 
обозначим δ - угол давления. Угол γ =90°-δ -угол передачи движения.
Сила F=Fд сosδ -сила полезных сопротивлений (сила тяжести, сила инерции, давления в пружине и т.д.). При расчетах сила F считается известной.
Сила H=Fд sinδ- сила вредных сопротивлений. Вызывает перекос толкателя, возникновение сил трения в направляющих. Если эта сила будет очень велика, может произойти заклинивание и поломка толкателя.
Рис.12.6
Для уменьшения силы H необходимо уменьшать угол давления δ. Однако, с другой стороны, с уменьшением угла δ возрастают размеры кулачка.
Динамическое условие записывается в виде:
δ≤δmax (12.1)
Принимают δmax =30°-для поступательно движущихся толкателей; δmax=45°-для вращающихся толкателей.
Кинематическому и динамическому условиям удовлетворяют три типа законов движения ведомого звена:
1.Законы, дающие постоянную скорость ведомого звена (рис.12.7).
За один оборот кулачка (φ=2π) толкатель проходит следующие фазы: φn-фаза подъема, φвв-фаза верхнего выстоя, φo- фаза опускания, φнв- фаза нижнего выстоя.
Скорость движения толкателя на фазах подъема и опускания постоянна. Ускорения на обеих фазах равны нулю, кроме положений а, в, с, и d, где функция Sz=f(φ1) имеет разрывы. В этих положениях теоретически ускорения ведомого звена, а, следовательно, и силы инерции являются равными бесконечности. Это вызывает появление в механизме так называемых жестких ударов. Практически, из-за наличия упругих деформаций и зазоров в кинематических парах ускорения (следовательно и силы инерции) имеют большую, но конечную величину. Это приводит к размыканию элементов высшей кинематической пары, соударению кулачка и толкателя, быстрому износу поверхностей в этих местах. Применяется данный закон при малых скоростях ведомого звена или только на части фаз подъема и опускания и в закон вводятся переходные кривые, позволяющие осуществить плавный переход на участках сопряжения двух линейных законов.
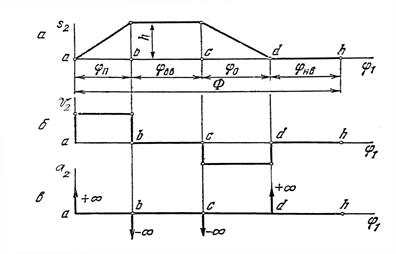
Рис.12.7
2.Законы, дающие постоянное ускорение ведомого звена (рис.12.8)
В этих законах ускорение в некоторых точках мгновенно изменяется на конечную величину, вызывая резкое изменение силы инерции, что ведет к появлению мягкого удара.
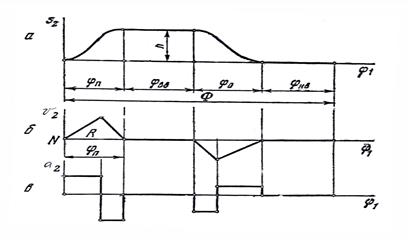
Рис.12.8
Безударные законы.
В этом случае кривая ускорений не имеет точек разрыва ни первого, ни второго рода (рис.12.9). Закон движения ведомого звена в этом случае может быть синусоидальным или косинусоидальным. Такие законы способствуют наибольшей работоспособности и долговечности кулачкового механизма.
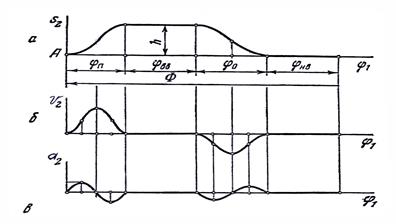
Рис.12.9
Дата добавления: 2016-03-05; просмотров: 633;