Экспоненциальное сглаживание.

Предположим, что временной ряд может быть представлен в виде:

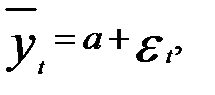
где а - const; 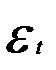— случайные неавтокоррелированные отклонения с нулевым математическим ожиданием и дисперсией .

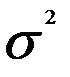Модель экспоненциального сглаживания ряда описывается следующей рекуррентной формулой:

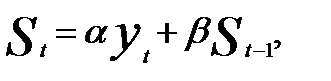(5.8)

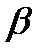где S_t — значение экспоненциальной средней в момент; — параметр сглаживания, = const, 0< < 1; = 1 - .

Если последовательно использовать соотношение (8.8), то экспоненциальную среднюю S_t можно выразить через предшествующие значения уровней временного ряда:

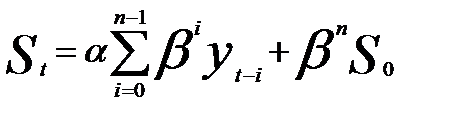(5.9)

где п — длина ряда; 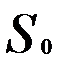— начальное значение экспоненциальной средней.

Из (5.2) видно, что величина S_t оказывается взвешенной суммой всех членов ряда. Причем веса отдельных уровней ряда убывают по мере их удаления в прошлое соответственно экспоненциальной функции (в зависимости от «возраста» наблюдений). Именно поэтому модель (5.8) получила название модели экспоненциального сглаживания.

Например, пусть = 0,1. Тогда вес текущего наблюдения 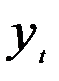, будет равен = 0,1, вес предыдущего уровня 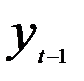будет соответствовать 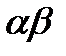= 0,1* 0,9 = 0,09; для уровня 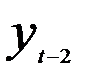вес составит 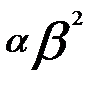= 0,081; для 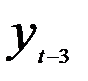— 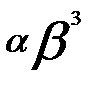= 0,0729 и т. д.

При расчете экспоненциальной средней в момент времени t всегда требуется значение экспоненциальной средней в предыдущий момент времени, поэтому на первом шаге должна быть определена некоторая

величина S₀, предшествующая 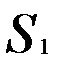. Часто на практике в качестве начального значения S₀ используется среднее арифметическое значение из всех имеющихся уровней временного ряда или из какой-то их части. Из выражения (8.9) следует, что вес, приписываемый этому значению, уменьшается по экспоненциальной зависимости по мере удаления от первого уровня. Поэтому для длинных временных рядов влияние неудачного выбора S₀ погашается.

Рассмотрим выражение (8.9) при п . Очевидно, что 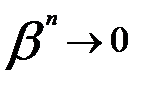, следовательно,

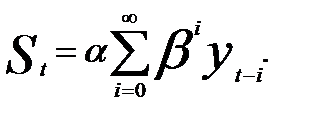(5.10)

Автор модели Р. Браун показал, что математические ожидания временного ряда и экспоненциальной средней совпадут, но в то же время дисперсия экспоненциальной средней D[S_t] будет меньше дисперсии временного ряда ( ).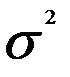

Представим выражение (5.10) в следующем виде:

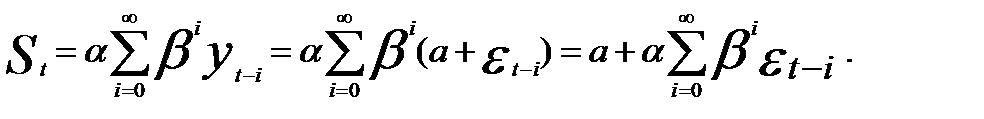
Отсюда очевидно, что математическое ожидание M(S_t) = a, так же как и математическое ожидание самого временного ряда.

Дисперсия экспоненциальной средней D[S_t] определяется выражением:

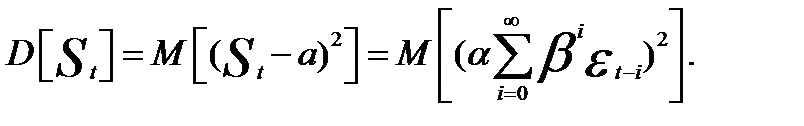
Учитывая свойства 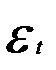можно записать:

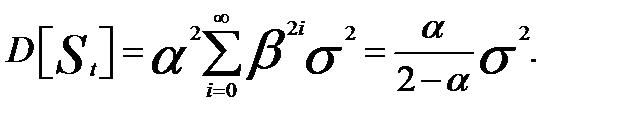
Таким образом, 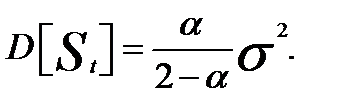(5.11)

Так как 0< <1, то D[S_t] будет меньше дисперсии временного ряда .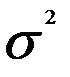

Из (5.11) видно, что при высоком значении дисперсия экспоненциальной средней незначительно отличается от дисперсии ряда. С уменьшением дисперсия экспоненциальной средней сокращается, возрастает ее отличие от дисперсии ряда. Тем самым экспоненциальная средняя начинает играть роль «фильтра», поглощающего колебания временного ряда.

Таким образом, с одной стороны, следует увеличивать вес более свежих наблюдений, что может быть достигнуто повышением , с другой стороны, для сглаживания случайных отклонений величину нужно уменьшить. Эти два требования находятся в противоречии. Поиск компромиссного значения параметра сглаживания с учетом специфики решаемой задачи составляет важную часть исследования.

ПРИМЕР 5.4

Требуется рассчитать экспоненциальную среднюю для временного ряда курса доллара США с 9 января 2013 г. по 6 февраля 2013 г. (табл. 5.5). В качестве начального значения экспоненциальной средней возьмите среднее значение пяти первых уровней. Расчеты проведите для трех различных значений параметров адаптации: а) = 0,2; б) = 0,5; в) = 0,8.

Сравните графически исходный временной ряд и экспоненциально сглаженные временные ряды при различных значениях параметра адаптации. Укажите, какой временной ряд носит более гладкий характер.

Решение.

Определим S₀ = .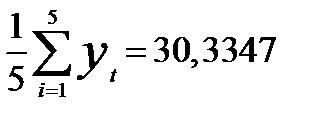

Найдем значения экспоненциальной средней при = 0,2.

Согласно (5.8)

Аналогичны вычисления для = 0,5 и = 0,8. Результаты расчетов экспоненциально сглаженных рядов при различных значениях параметров адаптации представлены в табл. 5.5.

Таблица 5.5

Экспоненциальные средние для временного курса доллара США

Дата	Порядковый номер уровня, t	Курс доллара США	Экспоненциальная средняя


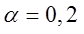
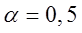
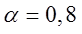
09.01.2013		30,3727	30,3423	30,3537	30,3651
10.01.2013		30,4215	30,3582	30,3876	30,4102
11.01.2013		30,3650	30,3595	30,3763	30,3740
14.01.2013		30,2537	30,3384	30,3150	30,2778
15.01.2013		30,2607	30,3228	30,2879	30,2641
16.01.2013		30,2556	30,3094	30,2717	30,2573
17.01.2013		30,3399	30,3155	30,3058	30,3234
18.01.2013		30,3431	30,321	30,3245	30,3392
21.01.2013		30,2065	30,2981	30,2655	30,2330
22.01.2013		30,2970	30,2979	30,2812	30,2842
23.01.2013		30,1950	30,2773	30,2381	30,2128
24.01.2013		30,2292	30,2677	30,2337	30,2259
25.01.2013		30,1648	30,2471	30,1992	30,1770
28.01.2013		30,0451	30,2067	30,1222	30,0715
29.01.2013		30,0782	30,181	30,1002	30,0769
30.01.2013		30,1513	30,1751	30,1257	30,1364
31.01.2013		30,0277	30,1456	30,0767	30,0494
01.02.2013		30,0161	30,1197	30,0464	30,0228
04.02.2013		29,9966	30,0951	30,0215	30,0018
05.02.2013		29,9251	30,0611	29,9733	29,9404
06.02.2013		30,1231	30,0735	30,0482	30,0866

На рис. 5.6 наглядно проявляется влияние значения параметра адаптации на характер сглаженного ряда. При = 0,2 экспоненциальная средняя носит более гладкий характер, так как в этом случае в наибольшей степени поглощаются случайные колебания временного ряда.

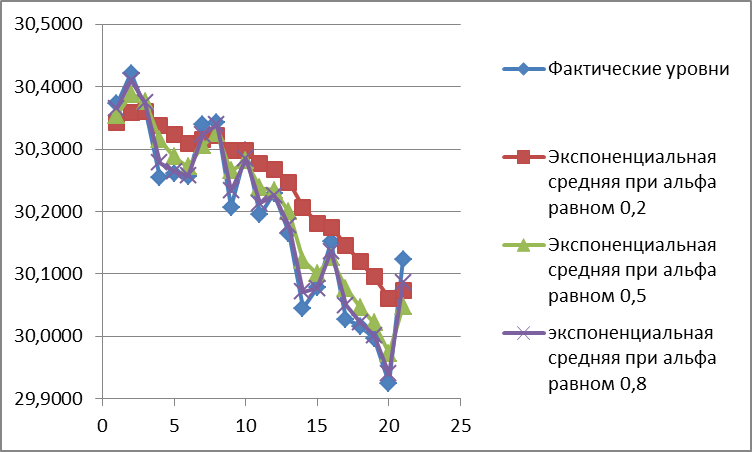
Рис.5.6. Экспоненциальное сглаживание временного ряда курса доллара США при различных значениях параметра адаптации

Выражение (5.8) можно представить по-другому, перегруппировав члены:

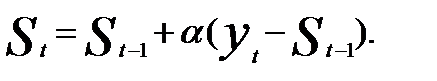
Величину (у _t - S_t_-1) можно рассматривать как погрешность прогноза. Тогда новый прогноз 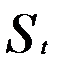получается в результате корректировки предыдущего прогноза с учетом его ошибки. В этом и состоит адаптация модели.

При краткосрочном прогнозировании желательно как можно быстрее отразить изменения ряда и в то же время очистить ряд, отфильтровав случайные колебания. Для этого величине следует присвоить одно из промежуточных значений в интервале от 0 до 1. Если в результате экспериментальных расчетов получено наилучшее значение , близкое к 1, то целесообразно проверить правомерность выбора модели данного типа. Р. Браун рекомендовал брать значения в пределах 0,1—0,3.

Иногда поиск этого значения параметра осуществляется путем перебора на сетке значений. В этом случае в качестве оптимального выбирается то значение а, при котором получена наименьшая дисперсия ошибки.

Следует отметить, что выбор значения параметра должен зависеть от периода упреждения прогноза. Для оперативных, конъюнктурных прогнозов в большей степени должна учитываться свежая информация, поэтому значение следует брать большим. При увеличении срока прогнозирования более поздняя информация, последние данные должны иметь несколько меньший вес, конъюнктурные колебания должны быть сглажены, но прошлые уровни — учтены. Для этих целей значение следует уменьшить.

Таким образом, экспоненциальное сглаживание является примером самообучающейся модели. К ее безусловным достоинствам относится чрезвычайная простота вычислений, выполняемых итеративно, причем массив прошлой информации уменьшен до единственного значения.

<22 23 242526 27 28 >

Дата добавления: 2016-03-22; просмотров: 1115;