Глава 3. Множественная корреляция и регрессия

3.1 Методы множественной корреляции и регрессии используются в тех случаях, когда набор рассматриваемых признаков разделяется на две части, одна из которых состоит из m признаков, образующих вектор

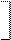X'= X₁, X₂, X₃, ..., X_m

а в другую - входит один показатель, который удобнее обозначить как Y. Такое обособление Y может быть вызвано конкретным видом задачи исследования. Необходимо рассмотреть корреляционную связь между признаком Y и набором других признаков X. Обычно признаки из вектора X называются независимыми переменными, а показатель Y - определяется как зависимая переменная.

В элементарной ситуации, когда набор признаков X включал только один показатель X, т.е. X = X задача, изучения корреляционной связи между Y и X предусматривает анализ двух ее аспектов. Первым из них является описание формы связи, которое заключается в определении зависимости между отдельными значениями признака X_i и соответствующим им средним уровнем признака Y. Эта задача решается при помощи построения так называемой теоретической линии регрессии Y_^i = f(X_i), где Y_^i - теоретическое среднее значение признака при условии того, что признак X принимает конкретное значение X_i и найденное в предположении, что корреляционная связь между значениями признаков Y и X_i может быть наилучшим образом описана функцией f(X).

Вторым аспектом корреляционной связи является ее теснота. Она позволяет сказать насколько велика вариация признака Y для отдельных наблюдений по отношению к линии регрессии. Эта изменчивость называется - остаточной и ее можно измерить соответствующей остаточной дисперсией S_yo². Мерой тесноты связи является так называемый индекс корреляции (теоретическое корреляционное отношение) величина которого определяется отношением остаточной дисперсии признака Y к общей дисперсии этого признака - S_yo²/ S_y². На основе такого отношения получается квадрат индекса корреляции в виде 1 - S_yo²/ S_y².

В подавляющем большинстве случаев корреляционные связи антропологических признаков могут быть вполне удовлетворительно описаны уравнением прямолинейной регрессии

Y_^i = a_o + a₁X_i , (3.1)

где a_o - свободный член этого уравнения, a₁ - так называемый коэффициент регрессии.

- 33 -

В качестве меры тесноты связей применяется частный случай индекса корреляции - коэффициент корреляции - r. На его основе можно получить значение остаточной дисперсии S_yo² = S_y²(1 - r²). Уравнению прямолинейной регрессии соответствует так называемая регрессионная модель

Y_i = Y_^i + u_i = a_o + a₁X_i + u_i, (3.2)

где Y_i - индивидуальное значение признака Y, которое можно представить как Y_^i + u_i. Компонент u_i называется регрессионным остатком и является отклонением реального значения Y_i от соответствующей ему регрессионной оценки Y_^i то есть - имеет вид Y_^i - - Y_i. Изменчивость остатков u_i измеряет дисперсия S_yo².