Проблема мультиколлинеарности
3.11 При вычислении параметров уравнения множественной регрессии по формулам (3.9), (3.17) и (3.21) необходимо находить матрицу обратную ковариационной S-1, корреляционной R-1 или произведению матрицы плана (D'D) -1, вычисляемых для независимых признаков. Однако, как следует из теории, операция обращения матрицы возможна только если ее определитель не равен нулю. В частности, если среди набора признаков, для которых вычислены матрицы S, R или D'D имеется хотя бы одна пара показателей, для которой коэффициент корреляции равен +1 или -1, их определители будут равны нулю, и операция обращения этих матриц окажется невозможной. Напротив, для набора нескоррелированных признаков определитель корреляционной матрицы достигнет своего максимального значения ½R½ = 1. В реальных случаях, когда все признаки имеют коэффициенты корреляции 0 < ½r½ < 1, обычно будет наблюдаться ситуация 0 < ½R½ < 1.
Однако, если среди набора независимых переменных X имеются признаки, связанные друг с другом высокой корреляцией с абсолютной величиной ее коэффициента близкой к 1, определители матриц S, R или D'D будут иметь малую величину. Хотя при этом нахождение S-1, R-1 или D'D-1 будет возможным, точность всех вычислений в регрессионном анализе резко уменьшится. Эта ситуация называется явлением мультиколлинеарности.
Наличие мультиколлинеарности приводит к резкой неустойчивости получаемых оценок параметров уравнений регрессии. Добавление или исключение какого-то отдельного наблюдения может приводить к сильному изменению всех регрессионных параметров. Очень сильно при этом могут также увеличиваться квадратические ошибки коэффициентов множественной регрессии, что приведет к невозможности доказать неслучайность
- 49 -
Таблица 3.8. Результаты применения процедуры пошаговой регрессии для множественной связи диаметра таза с другими размерами тела. Пятый шаг
| Признаки | Коэффициент корреляции | F- критерий включения | P |
| Складка живота | 0.124 * | 3.657 | 0.057 |
величины этих коэффициентов. Очевидно, ситуации мультиколлинеарности следует всячески избегать.
3.12 Для установления наличия мультиколлинеарности было предложено несколько приемов. Простейший из них заключается в предварительном рассмотрении корреляционной матрицы независимых признаков X. Если в ней имеются высокие коэффициенты корреляции ½rij½ > 0.8 - 0.9, тогда есть серьезные основания опасаться мультиколлинеарности.
Более точно это явление может быть установлено по значениям коэффициентов множественной корреляции Ri каждой i-й независимой переменной по остальным m - 1 таким переменным. Это можно сделать, последовательно применяя вычисления множественной регрессии и корреляции для каждого Xi по всем остальным независимым признакам X. Другой способ подобных вычислений заключается в определении матрицы R-1 обратной к корреляционной матрице R, вычисленной для всех независимых переменных. Тогда коэффициент множественной корреляции любого признака Xi по остальным показателям X может быть найден по формуле

 1 ½
1 ½
 Ri = 1 - , (3.29)
Ri = 1 - , (3.29)
r(ii)
где r(ii) - i-й диагональный элемент матрицы R-1. Очевидно, для признаков X, присутствие которых в наборе назависимых переменных вызывает мультиколлинеарность, величина коэффициента множественной корреляции Ri будет близка к 1.
Во многих пакетах компьютерных программ при вычислении множественной регрессии на основе таких коэффициентов Ri для каждого i-го независимого признака находится значение так называемой толерантности
Ti = (1 - Ri2) , (3.30)
которое содержится в выводимых результатах. Очевидно, что слишком малая толерантность у некоторого признака Xi свидетельствует о возможности эффекта мультиколлинеарности из-за его присутствия в наборе независимых переменных. Часто условием малости величин Ti считается Ti < 0.10. Для тех независимых признаков, у которых это условие выполняется, можно опасаться привнесения эффекта мультиколлинеарности.
Пример 3.3. При проведении пошаговой регрессии в состав набора независимых переменных были отобраны четыре информативных признака: длина корпуса, длина ноги, обхват груди и ширина лодыжки. Проверим возможность наличия в этом наборе явления мультиколлинеарности. В таблице 3.9 приведены параметры уравнения множественной регрессии ширины таза по этим четырем при знакам. Нетрудно видеть, что значения
- 50 -
Таблица 3.9. Результаты множественного регрессионного анализа ширины таза по 4 размерам тела по выборке 242 женщин
| Признак | Коэфффициенты регрессии | Стандартные ошибки | Толерантности | t- критерий | P |
| Свободный член | 16.130 | 30.042 | . | 0.537 | 0.592 |
| Длина корпуса | 0.059 | 0.029 | 0.941 | 2.027 | 0.044* |
| Длина ноги | 0.135 | 0.027 | 0.892 | 5.001 | 0.000* |
| Обхват груди | 0.167 | 0.015 | 0.858 | 11.170 | 0.000* |
| Ширина лодыжки | -0.560 | 0.273 | 0.799 | -2.054 | 0.041* |
толерантности у независимых переменных составляют 0.80 - 0.94 и весьма далеки от критического уровня 0.10. Поэтому, нам вряд ли следует опасаться наличия мультиколлинеарности.
3.13 После установления присутствия эффекта мультиколлинеарности следует попытаться от него избавиться. Этого можно добиться несколькими способами. Во-первых, следует исключить из набора независимых переменных те признаки, которые обнаруживают слишком высокую множественную связь с остальными показателями. Очень часто такими признаками могут быть некоторые размерные характеристики, являющиеся суммой или разностью других показателей, также участвующих в анализе. Очевидно, их устранение из рассмотрения не может привести к потере важной информации.
Применение пошаговой регрессии отбора информативных независимых переменных также способно привести к результатам без коллинеарности, так как при добавлении очередного признака в регрессионную модель в неявном виде оценивается величина его связи с уже включенными в нее показателями. Кроме этого часто при проведении вычислений явно учитывается величина толерантности (3.30) для каждого вновь включаемого в модель признака Xi. Если она слишком мала (обычно Ti < 0.10) то этот признак в уравнение регрессии не добавляется.
Наконец, можно попытаться перейти от набора сильно связанных независимых переменных с присутствующей для них мультиколлинеарностью к новым признакам, получаемым как линейные комбинации исходных, но обладающим взаимной нескоррелированностью. Такими новыми признаками, в частности, могут быть главные компоненты, свойства которых обсуждаются в главе 5. В результате множественная регрессия строится не по исходным мультиколлинеарным признакам, а - определяется для новых нескоррелированных переменных, для которых мультиколлинеарность заведомо отсутствует. При этом, в частности, можно добиться существенного уменьшения числа независимых переменных, так как, например, главные компоненты, обладают важным свойством, в соответствии с которым небольшое число этих новых признаков может описать основную долю (до 80-90%) всей суммарной информации об изменчивости исходных антропологических показателей.
- 51 -
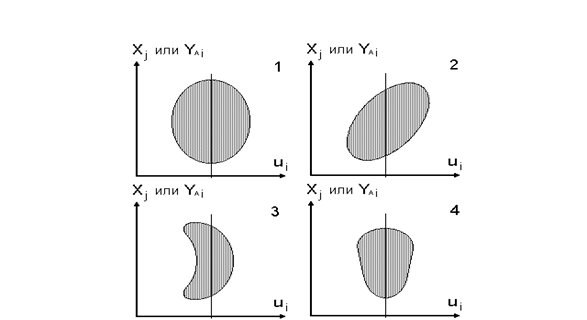
Рисунок 3.1. Возможные ситуации зависимости распределения величины остатков ui от значений некоторого признака Xi или регрессионных оценок Y^i: 1 - ситуация адекватности регрессионной модели, 2 - наличие линейной связи, 3 - наличие криволинейной связи, 4 - наличие гетероскедастичности
Дата добавления: 2016-02-13; просмотров: 1091;
