Анализ регрессионных остатков

3.14 Как уже говорилось в разделе 3.9, регрессионные остатки u_i, получаемые в модели

Y_i = a_o + a₁X_1i + a₂X_2i + ... a_mX_{m i} + u_i,

имеют вариацию (остаточную изменчивость), которая может считаться изменчивостью признака Y, свободной от связей с ним набора независимых признаков X. В дальнейшем индивидуальные значения этих остатков могут участвовать в дальнейшем содержательном анализе.

Однако, рассмотрение остаточной вариации может иметь также значение как анализ адекватности построенной регрессионной модели. Если она адекватна, то для остаточной изменчивости должно быть характерно выполнение ряда свойств. Во-первых, форма распределения остатков должна быть близкой к нормальному виду. Во-вторых, свойства этого распределения не должны зависеть от значений каких-либо независимых переменных X или от регрессионных оценок Y_^i зависимого показателя Y. Последнее означает, что для разных величин любого признака X_i или Y_^i у остатков не должно наблюдаться (рис.3.1) наличия корреляционной прямо- или криволинейной связи, а также - изменений величины вариации.

Большинство компьютерных статистических пакетов программ позволяет вычислять значения регрессионных остатков, записывать их в файлы, строить для них гистограммы или графики их зависимости от разных переменных X_i или регрессионных оценок Y_^i .

- 52 -

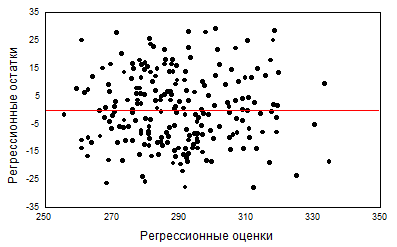
Рисунок 3.2. Зависимость регрессионных остатков от регрессионных оценок ширины таза по набору четырех независимых переменных

Даже визуальный анализ таких графиков позволяет обнаружить присутствие нежелательных эффектов, приведенных на рисунке 3.1. Так, наличие линейной связи значений остатков и величины признаков X_i или оценок Y_^i может указывать на ошибку в вычислениях. Появление эффекта криволинейности связи u_i с X_i или Y_^i означает необходимость введения в регрессионную модель квадратичного члена для X_i или проведения предварительного преобразования значений Y в виде lgY, Y^1/2 и др. Неодинаковая величина остаточной вариации (гетероскедастичность) также может потребовать предварительного преобразования (логарифмического, степенного и др.) значений зависимой переменной Y до проведения регрессионного анализа.

Пример 3.4. Рассмотрим изменчивость регрессионных остатков для регрессионной модели, уравнение которой было получено в примере 3.3. Для него были найдены индивидуальные значения остатков зависимой переменной - диаметра таза. На рисунке 3.2 приведены значения этих остатков u_i в зависимости от регрессионных оценок Y_^i. Нетрудно видеть, что какие-либо эффекты, свидетельствующие о наличии прямо- или криволинейной связи между u_i и Y_^i , а также - о гетероскедастичности, на этом графике не проявляются.

На рисунке 3.3 приведен аналогичный график, где показана вариация регрессионных остатков по отношению к одной из независимых переменных - длине ноги. Очевидно, что и здесь никаких нежелательных эффектов в поведении u_i не прослеживается. Аналогичные графики для остальных трех независимых признаков не приводятся.

- 53 -

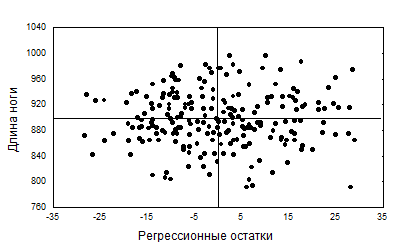
Рисунок 3.3. Зависимость регрессионных остатков от значений одной из независимых переменных - длины ноги для множественной регрессии ширины таза по набору четырех независимых переменных

3.15 Более подробно с регрессионными методами можно познакомиться по ряду обстоятельных руководств. Таковы книги Н.Дрейпера и Г.Смита (1973), Д.Се-бера (1980), Е.З.Демиденко (1981), А.Афифи и С.Эйзена, 1982, Э.Ферстера и Б.Ренца (1983), С.А.Айвазяна и др. (1985), И.Вучкова и др. (1987).