ИЗМЕНЧИВОСТИ НАБОРА ПРИЗНАКОВ

МНОГОМЕРНЫЕ МЕТОДЫ ИЗУЧЕНИЯ ВНУТРИГРУППОВОЙ

Определим изменчивость индивидов в группе, не обнаруживающей существенной внутренней структуры по тем факторам, которые могут заведомо вызывать разнокачественность состава этой группы (пол, возраст, этно-территориальная или профессиональная принадлежность и др.), как внутригрупповую изменчивость. При отсутствии внутренней структуры такой группы индивидов на первый план выступают закономерности вариации признаков и их взаимные корреляции. Из элементов описания, свойственных многомерному нормальному распределению, в таком случае может представлять интерес рассмотрение ковариационной матрицы или ее частного случая - корреляционной матрицы. Для этих целей разработан целый ряд методов. Их использование связано со смыслом поставленной задачи. В частности, одним из условий использования того или иного метода многомерного изучения корреляционных взаимосвязей признаков является структура набора этих изучаемых показателей.

В исследовательской практике возможна ситуация, когда вектор m признаков

X'= X₁, X₂, X₃, ..., X_m

содержательно значимым способом должен быть разбит на две части. Например, по тем или иным причинам один из этих признаков, скажем X_m, может быть выделен. Тогда набор признаков разобьется на две части

X'= X₁, X₂, X₃, ..., X_{m –1} | X_m = X_*' | X_m ,

где вектор X_*' включает признаки X₁, X₂, X₃, ..., X_{m –1} . Тогда изучение коррелированности признаков из целого набора X будет сведено к рассмотрению коррелированности признака X_m и набора признаков X_*. Такая задача естественным образом приводит к использованию так называемых методов множественной корреляции и регрессии. В этом случае изучается направленное воздействие признаков из их набора X_* на признак X_m.

Возможен иной способ содержательного разбиения набора признаков X на две части, когда каждая из них включает несколько переменных

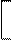
X'= X₁ X₂ X₃ ... X_n | X_n+1 X_n+2 ... X_m = X₁' | X₂' .

В этом случае целый вектор X можно представить как состоящий из двух частей X₁ и X₂. Первая из них включает первые n признаков, вторая - остальные m - n переменных. Тогда задача изучения взаимосвязей признаков из целого набора X сводится к рассмотрению корреляций двух наборов X₁ и X₂. Для подобных целей предназначается специальный метод канонических корреляций.

Наконец, возможна ситуация, когда общий набор признаков должен рассматриваться как нечто единое. Возможно существующая его внутренняя структура, предполагающая наличие групп признаков с относительно более высокими взаимными связями, в этом

- 32 -

случае должна выявляться по результатам проведенного анализа, а не предполагаться априорно. Для подобных целей используются методы компонентного и факторного анализа, которые при своей общей близости отличаются разными свойствами.

При использовании всех этих методов применяется широко распространенный в многомерной статистике прием получения новых переменных как линейных комбинаций исходных признаков. В зависимости от целей метода они называются каноническими переменными, главными компонентами или факторами и предназначены для явного выделения основных направлений изучаемых корреляций признаков.